1 简介 最近,已经提出了许多智能算法来寻找复杂工程问题的最佳解决方案。这些算法可以搜索易变的多维解空间,并及时找到最优答案。在本文中,提出了一种新的元启发式方法,该
1 简介
最近,已经提出了许多智能算法来寻找复杂工程问题的最佳解决方案。这些算法可以搜索易变的多维解空间,并及时找到最优答案。在本文中,提出了一种新的元启发式方法,该方法可以激发称为 Coot 的鸟群的行为。 Coot算法模拟了鸟类在水面上的两种不同运动方式:第一阶段,鸟类的运动是不规则的,第二阶段是有规律的。蜂群向一群领先的领导者移动以达到食物供应;蜂群末端的运动是一串coot的形式,每个coot都在其前面的coot后面移动。然后该算法在多个测试函数上运行,并将结果与众所周知的优化算法进行比较。此外,解决了拉压弹簧、压力容器设计、焊接梁设计、多片盘式离合器制动器、阶梯锥带轮问题、悬臂梁设计、减速器设计问题、滚动体轴承问题等几个实际问题该算法用于确认该算法的适用性。结果表明,该算法能够胜过大多数其他优化方法。
2 部分代码
% Developed in MATLAB R2017b% Source codes demo version 1.0
%
% You can find the COOT code at
% _____________________________________________________
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
clc
N=30; % Number of search agents
Function_name='F13'; % Name of the test function
Max_iter=500; % Maximum number of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Convergence_curve,gBest,gBestScore]=COOT(N,Max_iter,lb,ub,dim,fobj);
display(['The best location of COOT is: ', num2str(gBest)]);
display(['The best fitness of COOT is: ', num2str(gBestScore)]);
3 仿真结果
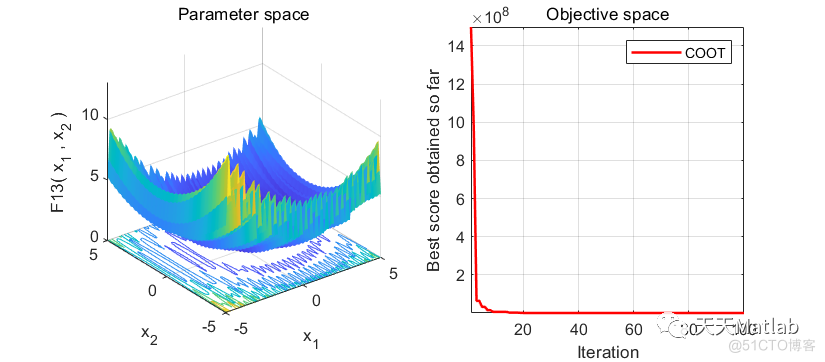
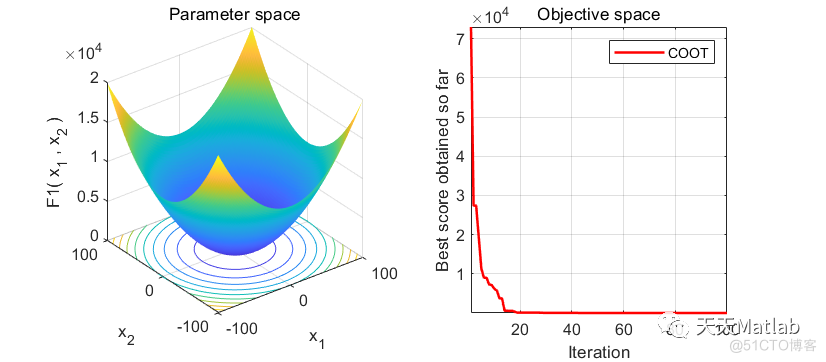
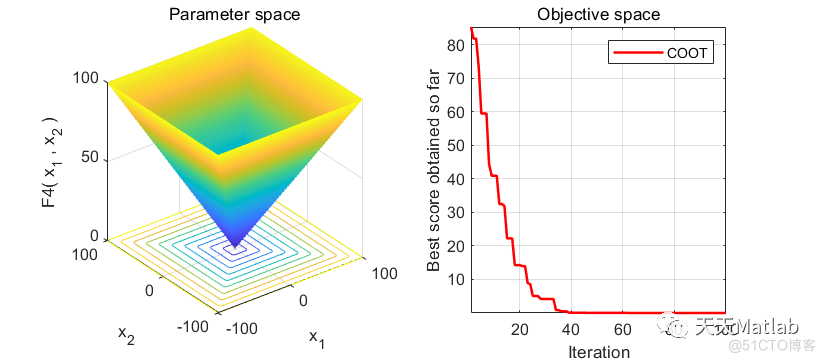
4 参考文献
[1] Naruei I , Keynia F . A New Optimization Method Based on Coot Bird Natural Life Model[J]. Expert Systems with Applications, 2021, 183(2):115352.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

