聚类算法的理想结果是同一类别内的点相似度高,而不同类别之间的点相似度低。聚类属于无监督学习,数据没有标签,为了比较不同聚类模型的好坏,我们也需要一些定量的指标来进行评估。根式是否提供样本的标签信息,相关的指标可以分为以下两大类
1. 外部方法,外部方法指的是从外部提供数据的标签,比如通过专家认为定义类别,或者是本身就是有标签的数据,将标签拿掉之后做聚类
2. 内部方法,内部方法指的是不需要数据的标签,仅仅从聚类效果本身出发,而制定的一些指标
本文主要关注外部方法,常用的指标有以下几种
1. Purity
称之为纯度,公式如下
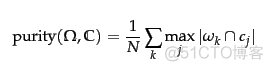
计算聚类正确的百分比,用每个簇内频数最高的样本类别作为正确的聚类,然后除以簇内的样本总数,通过一个例子来看下纯度的计算

整体的纯度就是(1/17)*(5+4+3)= 0.71, 从公式来看,纯度的值越高,聚类的性能越好,但是聚类的cluster个数越多,也会导致纯度值变高。所以无法直接使用纯度来表征聚类数量和聚类质量。
2. Normalized Mutual Information
简写为NMI, 称之为标准化互信息。首先来理解下互信息这个概念,互信息和熵是信息论的两个核心概念,互信息用于衡量两个信息之间的相关性,对于连个随机变量X和Y,互信息的公式如下
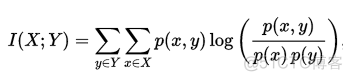
在概率论中, p(x, y)称之为联合概率,p(x), p(y)称之为边缘概率。互信息用于衡量其中一个变量对另一个变量不确定性减少的程度,下列推导证明了互信息和熵之间的关系
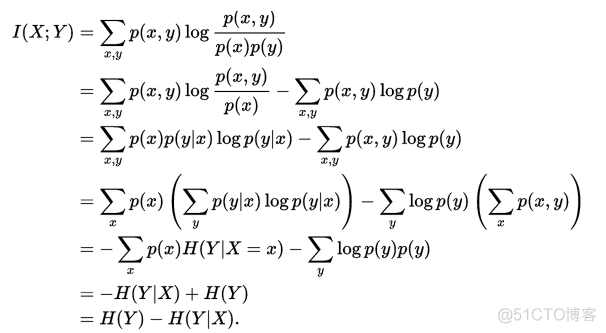
图示如下
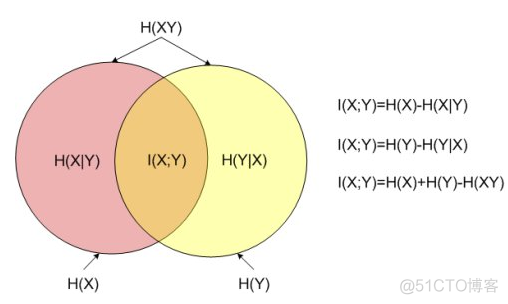
两个变量之间的互信息,可以看做是边缘熵熵减去条件熵,如果两个变量完全独立,则互信息为零。对于算法聚类结果和外部标签,可以通过统计如下所示的表格,来计算互信息
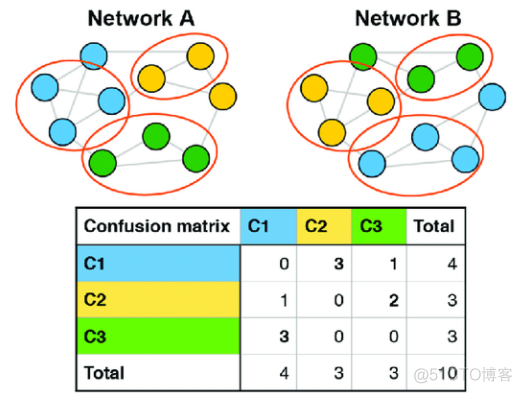
理论上,互信息的值越大越好,可是其取值范围是没有上边界的。为了更好的比较不同聚类结果,提出了标准化互信息的概念,公式如下
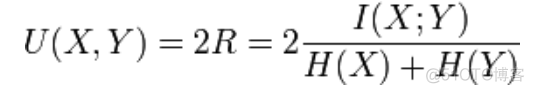
将互信息的值归一化到0和1之间,这样就可以在不同数据集之间进行比较了。标准化互信息的值越接近1,聚类效果越好。
3. Adjusted mutual information
简写为AMI, 称之为调整互信息,公式如下
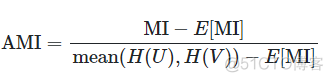
其中E表示期望值,对应的公式如下
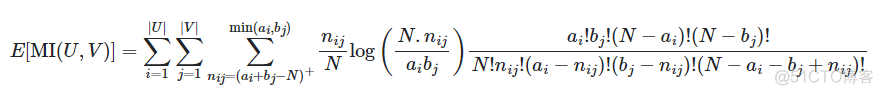
互信息和归一化互信息的值都会受到聚类的类别数K的影响,而AMI则不会受到干扰,取值范围为-1到1,数值越大,两种聚类结果越接近。
4. Rand index
简写为RI, 称之为兰德指数。对于两种模型的聚类结果,可以统计如下所示的表格
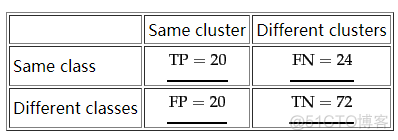
根据是否一致将结果分成两类,从而统计2X2的列联表,兰德指数就是根据上述表格进行计算的,公式如下

反映的是二种聚类结果中一致结果的百分比,取值范围为0-1,比例越大,说明聚类效果越好。
5. Adjusted Rand index
简写为ARI, 称之为调整兰德指数,借鉴AMI的概念,公式如下
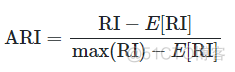
取值范围为-1到1,数值越大,聚类效果越好。
6. F scores
F值是一系列指标,通过引入参数β来定义具体的F值,公式如下

这里的F值就是分类模型评估中所采用的F值,通过外部标签,将聚类结果转换为分类结果来评估。
7. Fowlkes-Mallows scores
简写为FMI, 公式如下
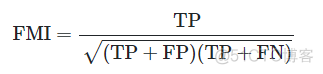
取值范围为0到1,越接近1,聚类效果越好。
8. V-measure
公式如下
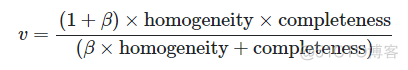
和F值类似,在公式中引入了一个自定义的参数β。要理解V-measure,首先来看下同质性homogeneity和完整性completeness两个概念,对应的公式如下
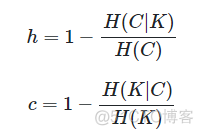
当β取值为1时,V-measure的公式如下
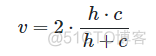
V-measure的取值范围为0-1,数值越大,聚类效果越好。
·end·

一个只分享干货的
生信公众号
