在多元线性回归中,多个变量之间可能存在多重共线性,所谓多重,就是一个变量与多个变量之间都存在线性相关。首先来看下多重共线性对回归模型的影响,假设一下回归模型
y = 2 * x1 + 3 * x2 + 4举一个极端的例子,比如x1和x2 这两个变量完全线性相关,x2=2*x1, 此时,上述回归方程的前两项可以看做是2个x1和3个x2的组合,通过x1和x2的换算关系,这个组合其实可以包括多种情况,可以看看做是8个x1, 4个x2, 也可以看做是4个x1和2个x2的组合,当然还有更多的情况
y = 8 * x1 +4y = 3 * x1 + 2 * x2 + 4
y = x1 + 3.5 * x2 + 4
y = 4 * x1 + 2 * x2 +4
y = 4 * x2 + 4
在x1和x2完全线性相关的情况下,以上方程都是等价的,在这里举这个完全线性相关的例子,只是为了方便理解当变量间存在线性相关时,对应的系数会相互抵消。此时,回归方程的系数难以准确估计。
在最小二乘法的求解过程涉及逆矩阵运算,一个矩阵可逆需要符合行列式不为零或者矩阵满秩,当变量存在多重共线性时,对应的矩阵不满秩,就会导致无法进行逆矩阵运算,也会对简单最小二乘法造成影响,尽管仍然可以通过伪逆矩阵运算来求解。
对于多重共线性的情况,如果执意用最小二乘法来求解,会发现,随着变量相关性的增强,回归系数的方差会变大,用一个示例的例子来验证一下,代码如下
>>> x = np.arange(0.6, 1.0, 0.05)>>> beta1 = []
>>> for i in x:
... data = np.array([[i, 2], [2, 4], [4, 8]])
... target = np.array([1, 2, 3])
... reg = linear_model.LinearRegression().fit(data, target)
... beta1.append(reg.coef_[0])
...
>>> plt.plot(x, beta1, 'o-')
[<matplotlib.lines.Line2D object at 0x13633580>]
>>> plt.show()
输出结果如下
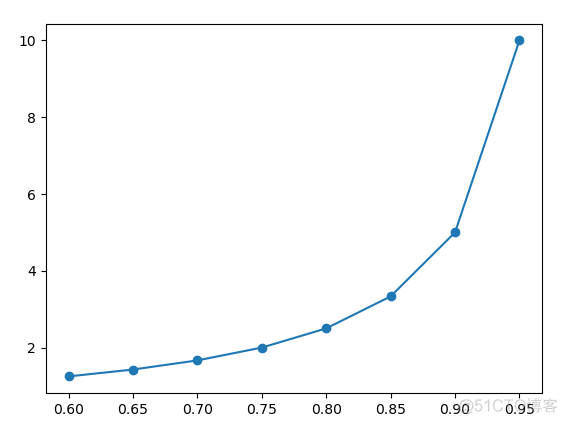
x轴是自变量的取值,x不断增大,上述拟合结果中的自变量之间的相关系数也不断增强,可以看到,随着相关性的增强,回归系数的变化速率越来越快。而对于两个完全独立的变量而言,而拟合结果是恒定不变的,方差为0,而多重共线性则导致拟合结果随着相关系数的变化而变化,回归系数的方差变大了。
为了解决多重共线性对拟合结果的影响,也就是平衡残差和回归系数方差两个因素,科学家考虑在损失函数中引入正则化项。所谓正则化Regularization, 指的是在损失函数后面添加一个约束项, 在线性回归模型中,有两种不同的正则化项
1.所有系数绝对值之和,即L1范数,对应的回归方法叫做Lasso回归,套索回归
2.所有系数的平方和,即L2范数,对应的回归方法叫做Ridge回归,岭回归
岭回归对应的代价函数如下
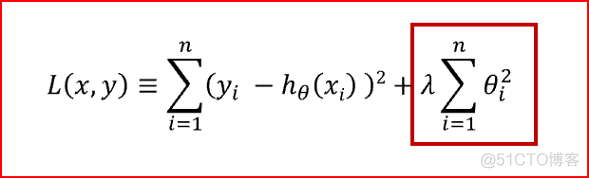
套索回归回归对应的代价函数如下
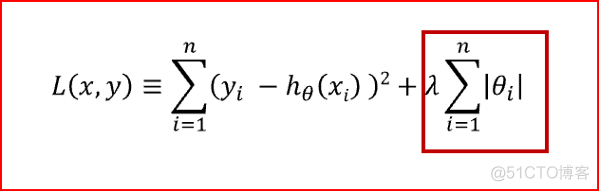
从上面的公式可以看出,两种回归方法共性的第一项就是最小二乘法的损失函数,残差平方和,各自独特的第二项则就是正则化项, 参数 λ 称之为学习率。
对于岭回归而言,可以直接对损失函数进行求导,在导数为0处即为最小值,直接利用矩阵运算就可以求解回归系数
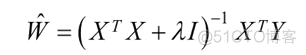
对于套索回归而言,损失函数在w=0出不可导,所以没法直接求解,只能采用近似法求解。在scikit-learn中,有对应的API可以执行岭回归和套索回归
1. 岭回归
>>> data = np.array([[0, 0], [0, 0], [1, 1]])>>> data
array([[0, 0],
[0, 0],
[1, 1]])
>>> target = np.array([0, 0.1, 1]).reshape(-1,1)
>>> target
array([[0. ],
[0.1],
[1. ]])
>>> from sklearn import linear_model
# 岭回归
>>> reg = linear_model.Ridge(alpha=.5).fit(data, target)
>>> reg
Ridge(alpha=0.5)
>>> reg.coef_
array([[0.34545455, 0.34545455]])
>>> reg.intercept_
array([0.13636364])
2. 套索回归
>>> reg = linear_model.Lasso(alpha=.5).fit(data, target)>>> reg
Lasso(alpha=0.5)
>>> reg.coef_
array([0., 0.])
>>> reg.intercept_
array([0.36666667])
对于这两种回归而言,学习率的设置对拟合结果有较大影响,在实际分析中,需要根据模型的验证效果来选取最佳的学习率值。为了更加方便的探究最佳学习率,内置了留一法交叉验证的API, 用法如下
>>> from sklearn.datasets import make_regression>>> X, y = make_regression(noise=4.0, random_state=0)
# 岭回归
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13)).fit(X, y)
>>> reg.alpha_
0.01
# 套索回归, 两种方法
# LassoCV
>>> reg = linear_model.LassoCV(cv=5).fit(X, y)
>>> reg
LassoCV(cv=5)
>>> reg.alpha_
0.3964179552011309
# LassoLarsCV
>>> reg = linear_model.LassoLarsCV(cv=5).fit(X, y)
>>> reg
LassoLarsCV(cv=5)
>>> reg.alpha_
0.048432240696248796
对于存在多重共线性的病态数据,可以使用岭回归和套索回归来限制多重共线性对拟合结果的影响。
·end·

一个只分享干货的
生信公众号
