时间序列模型算法 - ARIMA （一）

时间序列模型

• ​​1.时间序列模型概述​​

• ​​1.1 时间序列的不同分类​​
• ​​1.2 确定性时间序列分析方法概述​​
• ​​1.3 三种时间序列模型​​

• ​​2.指标平滑ES​​

• ​​2.1 一次指数平滑法​​

• ​​3.ACF与PACF​​
• ​​4.AR​​
• ​​5.MA​​
• ​​6.ARMA​​
• ​​7.ARIMA​​

• ​​7.1 差分​​

• ​​8. ARIMA实践​​

• ​​8.1 读取数据​​
• ​​8.2 画图，观察数据是否非平稳​​
• ​​8.3 差分，观察数据​​
• ​​8.4 单位根检验，确定数据为平稳时间序列​​
• ​​8.5 Q检验，检验是否数据具有相关性​​
• ​​8.6 确定AR和MA，画ACF、PACF判断​​
• ​​8.7 使用AIC、BIC最小准则确定p、q​​
• ​​8.8 拟合ARIMA或者ARMA模型​​
• ​​8.9 检验模型效果：残差检验​​
• ​​8.10 预测​​
• ​​8.11 将预测的平稳值还原为非平稳序列​​

1.时间序列模型概述

时间序列是研究数据随时间变化而变化的一种算法。是一种预测性分析算法。它的基本出发点就是事物发展都有连续性，按照它本身固有的规律进行。

时间序列的常用算法包括：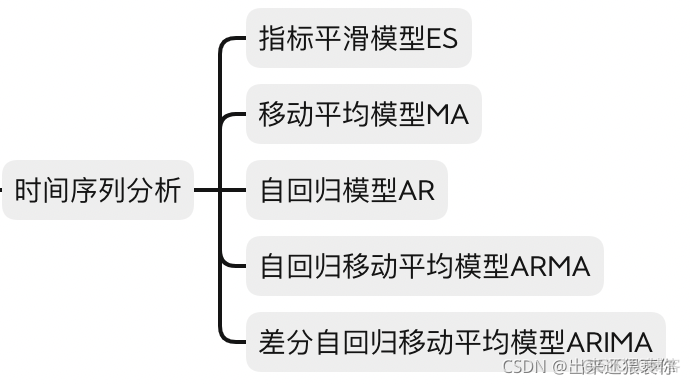

有这几个那如何选择模型呢

首先我们要知道时间序列就是按照时间顺序排列，随时间变化的随机过程，也就是说有对应的均值、方差、协方差等。
时间序列可以解决在只有时间（序列项）而没有其他可控变量下对未来数据的预测问题，常用于经济预测、股市预测、天气预测等。

如果随机过程随着时间变化，则此过程是非平稳的，相反，如果随机过程的特征不随时间变化，则此过程为平稳的

• 如果导致非平稳的原因确定：ES、MA、AR、ARMA
• 如果是平稳序列：ARIMA

1.1 时间序列的不同分类

时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。

时间序列根据研究的依据不同，可有不同的分类。

如果一个时间序列的概率分布与时间t无关，则称该序列为严格的（狭义）平稳时间序列。

如果序列的一、二阶矩存在，而且对任意时刻t满足：

（1）均值为常数

（2）协方差为时间间隔 T 的函数。则称为宽平稳（广义）时间序列。以后研究的时间序列主要是宽平稳时间序列。

1.2 确定性时间序列分析方法概述

一个时间序列可以分解为以下四部分：

（1）长期趋势变动。它指时间序列朝一定方向持续上升或下降，或停留在某一水平上，它反映了客观事物的主要变化趋势。

（2）季节变动。

（3）循环变动。通常指周期为一年以上，由非季节因素引起的波形相似的波动。

（4）不规则变动。通常为突然变动和随机变动。

1.3 三种时间序列模型

通常用 表示长期趋势项， 表示季节变动趋势项， 表示循环变动趋势项， 表示随机干扰项。常见的确定性时间序列模型有以下类型：

（1）加法模型

（2）乘法模型

（3）混合模型

其中 是观测目标的观测记录，， 。

2.指标平滑ES

2.1 一次指数平滑法

线性回归算法中，每个经验点的权重是一致的，即很早以前的经验数据也可能对预测数据有较大的影响。很多实际场景中，未来一段时间的趋势可能和在最近一段时间的趋势关系更加紧密。比如小明去年数学考试成绩一直不及格，今年连续多次考试90多分，预测小明下一次数学考试的成绩，情理上90多分的可能性更高。采用传统的线性回归算法，预测结果可能是70多分。

指数平滑法原则认为，时间越靠过去的经验数据对趋势的影响越小。我们假定时间t的观测值为y(t)，时间t的预测值为S(t)，则时间t+1的预测值S(t+1)为

a的取值范围在(0,1)，a越大，最近时间点的观测值对预测值的影响越大

另外还有二次指数平滑、三次指数平滑，就不介绍，懒得写

3.ACF与PACF

首先来说ACF与PACF是用来确定模型AR(p,)、MA(q,)、ARMA(p,q)、ARIMA(p,l,q)，中p、q。方法如下：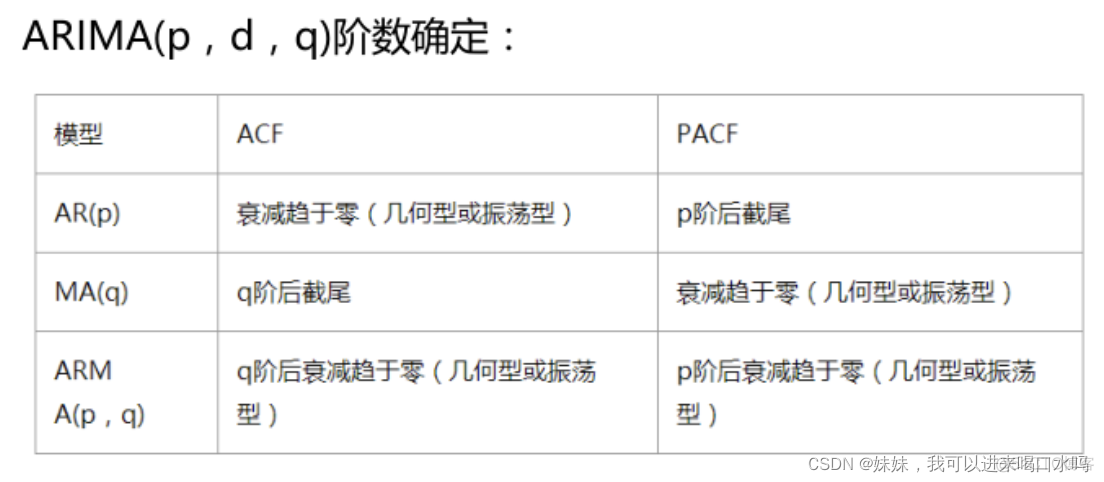

• 截尾：落在置信区间（95%的点都符合该规则）

如何用PACF图和ACF图来确定p、q值
通常我们确定了模型后，看模型的数据的阶数和2倍标准差范围。

这里先解释一下 阶数就是历史观测项，比如当前时间t数据为阶数为7，表示。