特色栏目： python 批处理 net编程 Javascript Php Asp Css Html5 Android seo centos

强化学习

来源：互联网收集：自由互联发布时间：2022-07-05

继续学习强化学习，介绍强化学习两大分支之一的价值学习，以及价值学习的一种经典实现方式DQN，以及DQN的训练算法TD learning. Value-Based Reinforcement Learning : 价值学习 2. 价值学习2.1 De

继续学习强化学习，介绍强化学习两大分支之一的价值学习，以及价值学习的一种经典实现方式DQN，以及DQN的训练算法TD learning.

Value-Based Reinforcement Learning : 价值学习

2. 价值学习 2.1 Deep Q-Network DQN

其实就是用一个神经网络来近似 $Q*$ 函数。

agent 的目标是打赢游戏，如果用强化学习的语言来讲，就是在游戏结束的时候拿到的奖励总和 Rewards 越大越好。

a. Q-star Function

问题：假设知道了 $Q^*(s,a)$ 函数，哪个是最好的动作？

显然，最好的动作是$a^* = \mathop{argmax}\limits_{a}Q^*(s,a)$ ，

$Q^*(s,a)$可以给每个动作打分，就像一个先知，能告诉你每个动作带来的平均回报，选平均回报最高的那个动作。

但事实是，每个人都无法预测未来，我们并不知道$Q^*(s,a)$。而价值学习就在于学习出一个函数来近似$Q^*(s,a)$ 作决策。

解决：Deep Q-network(DQN)，即用一个神经网络 $Q(s,a;w)$来近似 $Q^*(s,a)$ 函数。
神经网络参数是 w ，输入是状态 s，输出是对所有可能动作的打分，每一个动作对应一个分数。
通过奖励来学习这个神经网络，这个网络给动作的打分就会逐渐改进，越来越精准
玩上几百万次超级玛丽，就能训练出一个先知。

b. Example

对于不同的案例，DQN 的结构会不一样。

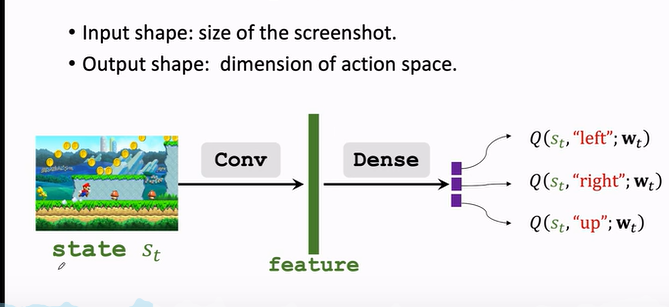
如果是玩超级玛丽

屏幕画面作为输入
用一个卷积层把图片变成特征向量
最后用几个全连接层把特征映射到一个输出的向量
输出的向量就是对动作的打分，向量每一个元素对应一个动作的分值，agent 会选择分值最大的方向进行动作。

c. 用 DQN 打游戏

DQN 的具体执行过程如下：

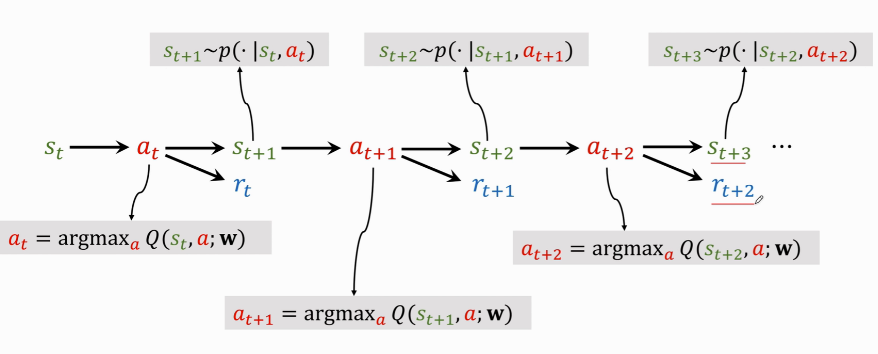
分步解释：

$ s_t \rightarrow a_t$：当前观测到状态 $s_t$，用公式 $ a_t=\mathop{argmax}\limits_{a}Q^*(s,a)$ 把 $s_t$ 作为输入，给所有动作打分，选出分数最高的动作 $a_t$ 。
agent 执行 $a_t$ 这个动作后，环境会改变状态，用状态转移函数 $p(\cdot|s_t,a_t)$ 随机抽样得出一个新状态 $s_{t+1}$。
环境还会告诉这一步的奖励 $r_t$ ，奖励就是强化学习中的监督信号，DQN靠这些奖励来训练。
有了新的状态 $s_{t+1}$，DQN 继续对所有动作打分，agent 选择分数最高动作 $a_{t+1}$。
执行 $a_{t+1}$ 后，环境会再更新一个状态 $s_{t+2}$，给出一个奖励 $r_{t+1}$。
然后不断循环往复，直到游戏结束

2.2 TD 学习

如何训练 DQN ？最常使用的是 Temporal Difference Learning。TD学习的原理可以用下面这个例子来展示：

a. 案例分析

要开车从纽约到亚特兰大，有一个模型$Q(w)$预测出开车出行的开销是1000分钟。这个预测可能不准，需要更多的人提供数据来训练模型使得预测更准。

问题：需要怎样的数据？如何更新模型。

出发之前让模型做一个预测，记作$q$，$q=Q(w)$，比如$q=1000$。到了目的地，发现其实只用了860分钟，获取真实值 $y=860$。
实际值$y$与预测值$q$有偏差，这就造成了 loss 损失
loss 定义为实际值与预测值的平方差：$L=\frac{1}{2}(q-y)^2$
对损失 $L$关于参数$w$求导并用链式法则展开：

$\frac{\partial L}{\partial w} = \frac{\partial q}{\partial w} \cdot \frac{\partial L}{\partial q} =(q-y)\cdot\frac{\partial Q(w)}{\partial w}$
梯度求出来了，可以用梯度下降来更新模型参数 w ：$w_{t+1} = w_t - \alpha \cdot \frac{\partial L}{\partial w} \vert _{w=w_t}$

缺点：这种算法比较 naive，因为要完成整个旅程才能完成对模型做一次更新。

那么问题来了：假如不完成整个旅行，能否完成对模型的更新？

可以用 TD 的思想来考虑这件事情。比如我们中途路过 DC 不走了，没去亚特兰大，可以用 TD 算法完成对模型的更新，即

出发前预测：NYC -> Atlanta 要花1000分钟，这是预测值。

到了 DC 时，发现用了 300 分钟，这是真实观测值，尽管它是针对于部分的。
模型这时候又告知，DC -> Atlanta 要花 600 分钟。
模型原本预测：$Q(w) = 1000 $，而到 DC 的新预测：300 + 600 = 900，这个新的 900 估值就叫 TD target 。

这些名词要记住，后面会反复使用，TD target 是使用了 TD算法的道德整体预测值。
TD target $y=900$虽然也是个估计预测值，但是比最初的 1000 分钟更可靠，因为有事实成分。
把 TD target $y$ 就当作真实值：$L = \frac{1}{2}(Q(w)-y)^2$, 其中$Q(w) - y $称为TD error。
求导：$\frac{\partial L}{\partial w} =(1000-900)\cdot\frac{\partial Q(w)}{\partial w}$
梯度下降更新模型参数 w ：$w_{t+1} = w_t - \alpha \cdot \frac{\partial L}{\partial w} \vert _{w=w_t}$

b. 算法原理

换个角度来想，TD 的过程就是这样子的：

模型预测 NYC -> Atlanta = 1000, DC -> Atlanta = 600，两者差为400，也就是NYC -> DC = 400，但实际只花了300分钟预计时间与真实时间之间的差就是TD error：$\delta = 400-300 = 100$。

TD 算法目标在于让 TD error 尽量接近 0 。

即我们用部分的真实修改部分的预测，而使得整体的预测更加接近真实。我们可以通过反复校准可知的这部分真实来接近我们的理想情况。

c. 用于 DQN (1) 公式引入

上述例子中有这样一个公式：$T_{NYC\rightarrow ATL} \approx T_{NYC\rightarrow DC} + T_{DC\rightarrow ATL} $

想要用 TD 算法，就必须要用类似这样的公式，等式左边有一项，右边有两项，其中有一项是真实观测到的。

而在此之前，在深度强化学习中也有一个这样的公式：$Q(s_t,a_t;w)=r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w)$。

公式解释：

左边是 DQN 在 t 时刻做的估计，这是未来奖励总和的期望，相当于 NYC 到 ATL 的预估总时间。

右边 $r_t$是真实观测到的奖励，相当于 NYC 到 DC 。

$Q(s_{t+1},a_{t+1};w)$ 是 DQN 在 t+1 时刻做的估计，相当于 DC 到 ATL 的预估时间。

(2) 公式推导

为什么会有一个这样的公式？

回顾 Discounted return: $U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots$

提出 $\gamma$ 就得到 $ = R_t + \gamma(R_{t+1}+ \gamma R_{t+2}+ \gamma^2 R_{t+3}+\cdots) $

后面这些项就可以写成$U_{t+1}$,即 $=R_t+\gamma U_{t+1}$

这样就得到：$U_t = R_t + \gamma \cdot U_{t+1}$

直观上讲，这就是相邻两个折扣算法的数学关系。

(3) 应用过程

现在要把 TD 算法用到 DQN 上

t 时刻 DQN 输出的值 $Q(s_t,a_t; w)$ 是对 $U_t$ 作出的估计 $\mathbb{E}[U_t]$，类似于 NYC 到 ATL 的预估总时间。
下一时刻 DQN 输出的值 $Q(s_{t+1},a_{t+1}; w)$ 是对 $U_{t+1}$ 作出的估计 $\mathbb{E}[U_{t+1}]$，类似于 DC 到 ATL 的第二段预估时间。
由于 $U_t = R_t + \gamma \cdot U_{t+1}$
所以 $\underbrace{Q(s_t,a_t; w) }_{\approx\mathbb{E}[U_t]}\approx \mathbb{E}[R_t+\gamma \cdot \underbrace{Q(s_{t+1},a_{t+1}; w)}_{\approx\mathbb{E}[U_{t+1}]}]$
$\underbrace{Q(s_t,a_t;w)}_{prediction}=\underbrace{r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w)}_{TD\ \ target}$

有了 prediction 和 TD target ，就可以更新 DQN 的模型参数了。

t 时刻模型做出预测 $Q(s_t,a_t;w_t)$；
到了 t+1时刻，观测到了真实奖励 $r_t$ 以及新的状态 $s_{t+1}$，然后算出新的动作 $a_{t+1}$。
这时候可以计算 TD target 记作 $y_t$，其中$y_t=r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w）$
t+1 时刻的动作 $a_{t+1}$怎么算的？DQN 要对每个动作打分，取分最高的，所以等于Q 函数关于a求最大化：$ y_t = r_t + \gamma \cdot \mathop{max}\limits_{a} Q(s_{t+1},a;w_t）$
我们希望预测$Q(s_{t},a_{t};w)$尽可能接近 TD target $y_t$ ，所以我们把两者之差作为 Loss :

$L_t=\frac{1}{2}[Q(s_{t},a_{t};w)-y_t]^2$
做梯度下降：$w_{t+1} = w_t - \alpha \cdot \frac{\partial L}{\partial w} \vert _{w=w_t}$更新模型参数 w，来让 Loss 更小

2.3 总结

价值学习（本讲是DQN）基于最优动作价值函数 Q-star ：

$Q^*(s_t,a_t) = \mathbb{E}[U_t|S_t=s_t,A_t=a_t]$

对 $U_t$ 求期望，能对每个动作打分，反映每个动作好坏程度，用这个函数来控制agent。
DQN 就是用一个神经网络$Q(s,a;w)$来近似$Q^*(s,a) $
1. 神经网络参数是 w ，输入是 agent 的状态 s
2. 输出是对所有可能动作 $ a \in A$ 的打分
TD 算法过程
1. 观测当前状态 $S_t = s_t $ 和已经执行的动作 $A_t = a_t$
2. 用 DQN 做一次计算，输入是状态 $s_t$，输出是对动作 $a_t$ 的打分
  
  记作$q_t$，$q_t = Q(s_t,a_t;w)$
3. 反向传播对 DQN 求导：$d_t = \frac{\partial Q(s_t,a_t;w)}{\partial w} |_{ w=w_t}$
4. 由于执行了动作 $a_t$，环境会更新状态为 $s_{t+1}$，并给出奖励$r_t$。
5. 求出TD target：$y_t = r_t + \gamma \cdot \mathop{max}\limits_{a} Q(s_{t+1},a_t;w）$
6. 做一次梯度下降更新参数 w , $w_{t+1} = w_t - \alpha \cdot (q_t-y_t) \cdot d_t$
7. 更新迭代...

x. 参考教程

视频课程：深度强化学习（全）_哔哩哔哩_bilibili
视频原地址：https://www.youtube.com/user/wsszju
课件地址：https://github.com/wangshusen/DeepLearning
笔记参考：
- https://zlq7m64rhg.feishu.cn/drive/folder/fldcnvII4pZn6rjElhDTte1O7yD
- 价值学习：https://zlq7m64rhg.feishu.cn/docs/doccn4snBoFarcY7loAJhI7Jbk7

【文章原创作者：华为云代理 http://www.558idc.com/hw.html处的文章,转载请说明出处】

上一篇：Java开发学习(七)
下一篇：没有了

强化学习

相关文章