带你系统学习并且自己动手写一个自己的哈希表，从哈希表的整体设计，再到细节哈希函数、哈希冲突和扩容设计，内容精彩至极！！！
HashMap（Python字典）设计原理与实现（上篇）——哈希表的原理
在此前的四篇长文当中我们已经实现了我们自己的ArrayList和LinkedList，并且分析了ArrayList和LinkedList的JDK源代码。 本篇文章主要跟大家介绍我们非常常用的一种数据结构HashMap，在本篇文章当中主要介绍他的实现原理，下篇我们自己动手实现我们自己的HashMap，让他可以像JDK的HashMap一样工作。
如果有公式渲染不了，可查看这篇内容相同且可渲染公式的文章
HashMap初识如果你使用过HashMap的话，那你肯定很熟悉HashMap给我们提供了一个非常方便的功能就是键值(key, value)查找。比如我们通过学生的姓名查找分数。
public static void main(String[] args) {
HashMap<String, Integer> map = new HashMap<>();
map.put("学生A", 60);
map.put("学生B", 70);
map.put("学生C", 20);
map.put("学生D", 85);
map.put("学生E", 99);
System.out.println("学生B的分数是：" + map.get("学生B"));
}
我们知道HashMap给我们提供查询get函数功能的时间复杂度为O(1)，他在常数级别的时间复杂度就可以查询到结果。那它是如何做到的呢？
我们知道在计算机当中一个最基本也是唯一的，能够实现常数级别的查询的类型就是数组，数组的查询时间复杂度为O(1)，我们只需要通过下标就能访问对应的数据。比如我们想访问下标为6的数据，就可以这样：
String[] strs = new String[10];
strs[6] = "一无是处的研究僧";
System.out.println(strs[6]);
因此我们要想实现HashMap给我们提供的O(1)级别查询的时间复杂度的话，就必须使用到数组，而在具体的HashMap实现当中，比如说JDK底层也是采用数组实现的。
我们实现的HashMap需要满足的最重要的功能是根据键(key)查询到对应的值(value)，比如上面提到的根据学生姓名查询成绩。
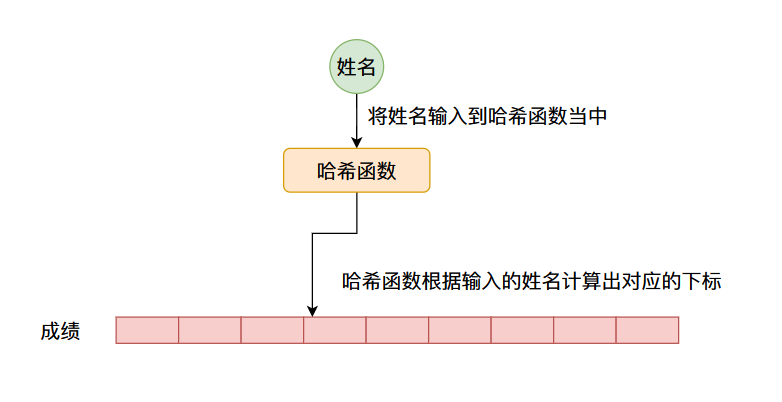
因此我们可以有一个这样的设计，我们可以根据数据的键值计算出一个数字（像这种可以将一个数据转化成一个数字的叫做哈希函数，计算出来的值叫做哈希值我们后续将会仔细说明），将这个哈希值作为数组的下标，这样的话键值和下标就有了对应关系了，我们可以在数组对应的哈希值为下标的位置存储具体的数据，比如上面谈到的成绩，整个流程如下图所示：
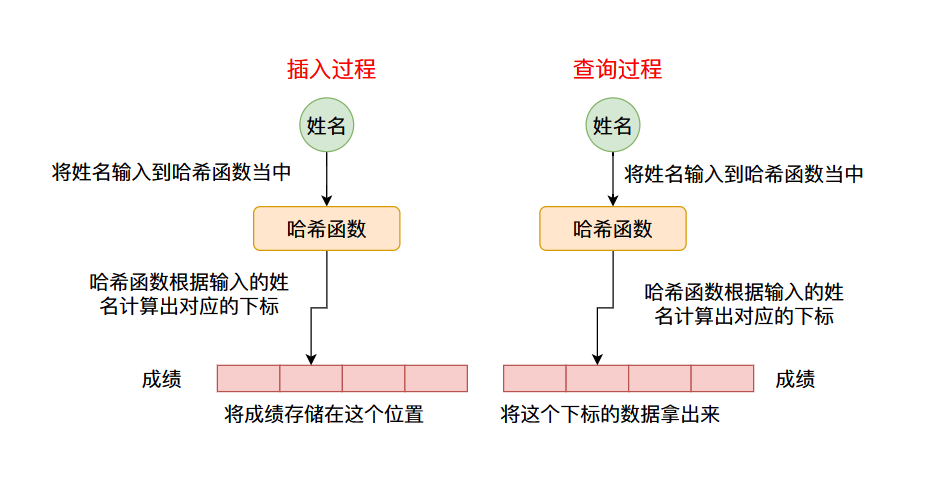
但是像这种哈希函数计算出来的数值一般是没有范围的，因此我们通常通过哈希函数计算出来的数值通常会经过一个求余数操作(%)，对数组的长度进行求余数，否则求出来的数值将超过数组的长度。比如数组的长度是16，计算出来的哈希值为186，那么求余数之后的结果为186%16=10，那么我们可以将数据存储在数组当中下标为10的位置，下次我们来取的时候就取出下标为10位置的数据即可。
首先我们需要了解一个知识，那就是在计算机世界当中我们所含有的两种最基本的数据类型就是，整型(short, int, long)和字符串(String)，其他的数据类型可以由这些数据类型组合起来，下面我们来分析一下常见的数据类型的哈希函数设计。
对于整型数据，他本来就是一个数值，因此我们可以直接将这个值返回作为他的哈希值，而JDK中也是这么实现的！JDK中实现整型的哈希函数的方法：
/**
* Returns a hash code for a {@code int} value; compatible with
* {@code Integer.hashCode()}.
*
* @param value the value to hash
* @since 1.8
*
* @return a hash code value for a {@code int} value.
*/
public static int hashCode(int value) {
return value;
}
我们知道字符串底层存储的还是用整型数据存储的，比说说字符串hello world，就可以使用字符数组['h', 'e', 'l', 'l', 'o' , 'w', 'o', 'r', 'l', 'd']进行存储，因为我们计算出来的这个哈希值需要尽量不和别的数据计算出来的哈希值冲突（这种现象叫做哈希冲突，我们后面会仔细讨论这个问题），因此我们要尽可能的充分利用字符串里面的每个字符信息。我们来看一下JDK当中是怎么实现字符串的哈希函数的
public int hashCode() {
// hash 是 String 类当中一个私有的 int 变量，主要作用即存储计算出来的哈希值
// 避免哈希值重复计算 节约时间
int h = hash; // 如果是第一次调用 hashCode 这个函数 hash 的值为0，也就是说 h 值为 0
// value 就是存储字符的字符数组
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
// 更新 hash 的值
hash = h;
}
return h;
}
上面的计算hashCode的代码，可以用下面这个公式表示：
- 其中
s，表示存储字符串的字符数组 n表示字符数组当中字符的个数
比如我们自己定义了一个学生类，我们改设计他的哈希函数，并且计算他的哈希值呢？
class Student {
String name;
int grade;
}
我们可以根据上面提到的两种哈希函数，仿照他们的设计，设计我们自己的哈希函数，比如像下面这样。
class Student {
String name;
int grade;
// 我们自己要实现的哈希函数
@Override
public int hashCode() {
return name.hashCode() * 31 + grade;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Student student = (Student) o;
return grade == student.grade &&
Objects.equals(name, student.name);
}
}
事实上JDK也贴心的为我们实现了一个类，去计算我们自定义类的哈希函数。
// 下面这个函数是我们自己设计的类 Student 的哈希函数
@Override
public int hashCode() {
return Objects.hash(name, grade);
}
// 下面这个函数为 Objects.hash 函数
public static int hash(Object... values) {
return Arrays.hashCode(values);
}
// 下面这个函数为 Arrays.hashCode 函数
public static int hashCode(Object a[]) {
if (a == null)
return 0;
int result = 1;
for (Object element : a)
result = 31 * result + (element == null ? 0 : element.hashCode());
return result;
}
JDK帮助我们实现的哈希函数，本质上就是将类当中所有的字段封装成一个数组，然后像计算字符串的哈希值那样去计算我们自定义类的哈希值。
其实集合类型的哈希函数也可以像字符串那样设计哈希函数，我们来看一下JDK内部是如何实现集合类的哈希函数的。
public int hashCode() {
int hashCode = 1;
// 遍历集合当中的对象，进行哈希值的计算
for (E e : this)
hashCode = 31*hashCode + (e==null ? 0 : e.hashCode());
return hashCode;
}
上述代码也可以用之前的公式来表示，其中s[i]表示集合当中第i个数据对象：
因为我们用的最终的数组的下标是通过哈希值取余数得到的，那么就有可能产生冲突。比如说我们的数组长度为10，有两个数据他们的哈希值分别为8和28，他们对10取余之后得到的结果都为8那么改如何解决这个问题呢？
假设我们的哈希函数为H，我们的数组长度为m，我们的键为key，那么我计算出来的下标为：
当我们有哈希冲突的时候，我们计算下标的方法变为：
\[h_i = (H(key) + d_i) \% m, d_i = i \]当我们第一次冲突的时候\(d_1 = 1\)，如果重新进行计算仍然冲突那么\(d_2 = 2\) ......
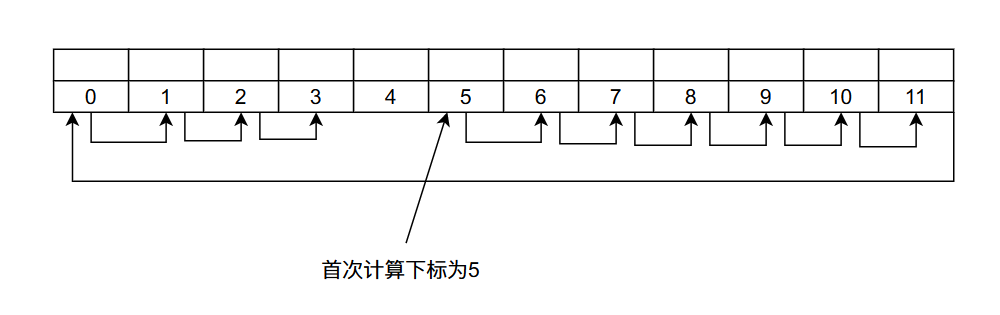
比如在上图当中我们首次计算的哈希值\(H(key) = 5\)的结果等于5，如果有哈希冲突，那么下次计算出来的哈希值为\((H(key) + 1) \% 12 = 6\)，如果还是冲突那么计算出来的哈希值为\((H(key) + 2) \% 12 = 7\) ......，直到找到一个空位置。谈到这里你可能会问，万一都满了呢？我们在下一小节再谈这个问题。
二次探测再散列 \[h_i = (H(key) + d_i) \% m, d_i = (-1)^{i - 1} i^2 \]这个散列方法和线性探测散列差不多，只不过\(d_i\)的值变化情况不一样而已，大家可以参考线性探测进行分析，这个方法可以往数组的两个方法走，因为前面有一个而线性探测只能往数组的一个方向走。此外这个方法走的距离比线性探测更大，因此可能可以在更小的冲突次数当中找到一个空位置。
这个方式的大致策略和前面差不多，只不过\(d_i\)上稍微有所差异。
再哈希法我们可以准备多个哈希函数，当使用一个哈希函数产生冲突的时候，我们可以换一个哈希函数，希望通过不同的哈希函数得到不同的哈希值，以解决哈希冲突的问题。
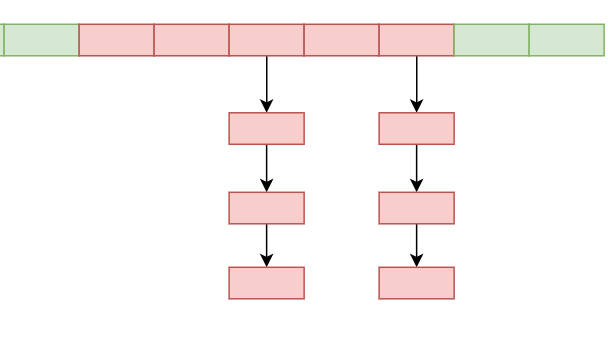
链地址法这个方法是目前使用比较多的方法，当产生哈希冲突的时候，数据用一个链表将冲突的数据链接起来，比如像下面这样：
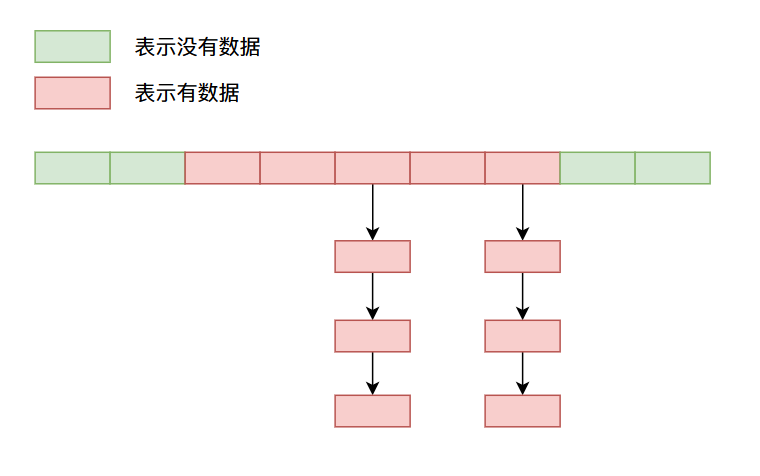
以上就是一些常见的解决哈希冲突的方法，因为都是文字说明没有代码，你可能稍微有些难以理解，比如说我通过上面的方法存储数据，那么我之后怎么拿到我存进去的数据呢？好像放进去就拿不出来了呀