排序算法之——希尔排序分析

引言

希尔排序的名称来源于它的发明者Donald Shell，是插入排序的一种，也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。

思路

希尔排序将整个待排序序列视为一个矩阵，逐列各自进行(插入)排序​​w-sorting​​。

若矩阵当前宽度为​​w​​​,那么各自排序称为​​w-sorting​​

过程：

• 将整个无序序列分割成若干个子序列（重排矩阵，由相隔某个“增量”的元素组成的）分别进行直接插入排序(若矩阵的每一列都已经经过了排序，则称之为​​w-ordered​​)
• 然后依次缩小增量再进行排序(使矩阵变窄)，待整个序列中的元素基本有序时，再对全体元素进行一次直接插入排序(如此往复，直到矩阵变成一列​​1-sorting​​)
• 其中，增量为矩阵宽度构造的逆序列

下面来分析一个实例：

数组大小为13，我们将增量初始设置为长度/2，然后不停的除2直到为0。

首先，宽度13/2 = 6，那么矩阵宽度为6，首先将一维数组构造成一个矩阵，列数为6，行数未知。

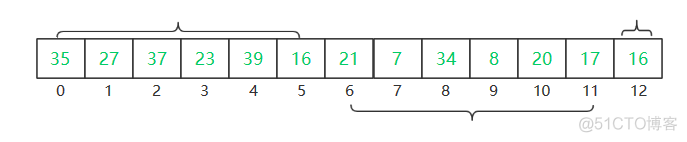
构造方法也很简单，取6个元素放在第1行，再取6个放在第2行…

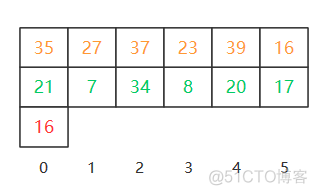
构造成的矩阵如上，每行给定不同的颜色，为了区分。初始数组可以看出是13X1的矩阵，这里我们把它变成了类似6X3的矩阵(为什么说类似，因为第3行没填满嘛)。

逐列进行(插入)排序​​6-sorting​​：

上图左边是插入排序后的结果，右边是矩阵还原成一维数组的结果。注意到我们的数组中有两个16，经过此次排序，最后一个16到了最前面，因此可以看出该算法是不稳定的。

宽度6/2=3：

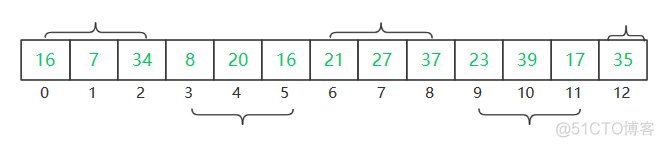
转换为矩阵，并排序：

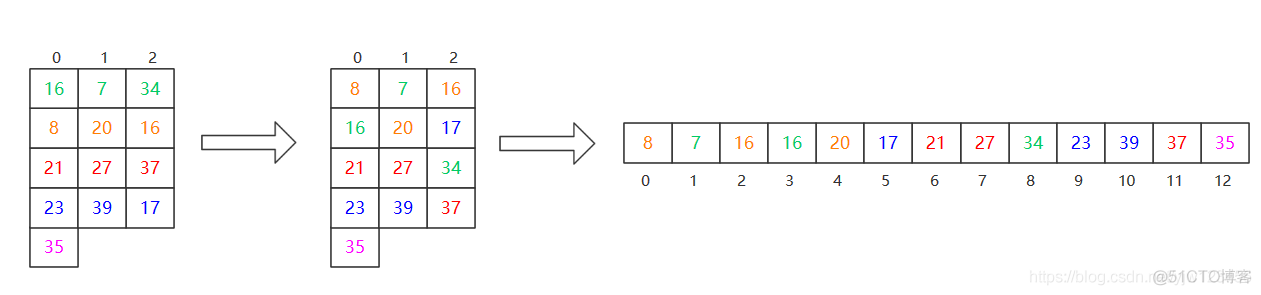
上图1转换矩阵；图2对每列进行排序；图3是转换成数组。可以感受到，进行插入排序并不需要交换太多的元素。插入排序很适合于这种基本有序的数组。

宽度3/2=1：

宽度为1的矩阵可以看成是立起来的一维数组，所以现在只需要对该数组进行插入排序即可。

最终结果为：

其中，橙色的元素是发生往前插的元素。最终，得到一个排序序列。

代码

/**
* 是插入排序的一种，也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。
* <p>
* 将整个无序序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，
* 然后依次缩小增量再进行排序，待整个序列中的元素基本有序时，再对全体元素进行一次直接插入排序。
* <p>
* 初始增量为数组长度/2，然后增量不停的缩小一半，直到为0
* @param a
* @param <E>
*/
public static <E extends Comparable<? super E>> void shellSort(E[] a) {
int j;
for (int gap = a.length/2; gap > 0 ; gap/= 2) {//初始增量为数组长度/2，然后增量不停的缩小一半，直到为0
for (int i = gap; i < a.length; i++) {//子序列分别进行直接插入排序
//进行直接插入排序
E tmp = a[i];
for (j = i; j >= gap && tmp.compareTo(a[j - gap]) < 0 ; j-= gap) {
a[j] = a[j - gap];
}
a[j] = tmp;
}
// System.out.println("gap=" + gap +"," + Arrays.toString(a));
}
}

其中，该部分代码是和直接插入排序很类似的，因此先要理解插入排序的思想。

E tmp = a[i];
for (j = i; j >= gap && tmp.compareTo(a[j - gap]) < 0 ; j-= gap) {
a[j] = a[j - gap];
}
a[j] = tmp;

复杂度和稳定性

• 时间复杂度
  希尔排序中对于增量序列的选择十分重要，直接影响到希尔排序的性能。我们上面选择的增量序列，其最坏时间复杂度依然为，一些经过优化的增量序列如Hibbard,经过证明可使得最坏时间复杂度为，。
• 稳定性
  非稳定算法