特色栏目： python 批处理 net编程 Javascript Php Asp Css Html5 Android seo centos

求本原根

来源：互联网收集：自由互联发布时间：2022-07-19

本原根本原根/原根/生成元从定义能看出，求本原根就是给定 $m$ ，求 $a$ 。 a模p的阶如果 $a$ 不被素数 $p$ 整除，则 $a$ 模 $p$ 的阶是指使得 $a^e=1（mod p）$ 的最小指数 \(e=1

本原根

本原根/原根/生成元

从定义能看出，求本原根就是给定$m$，求$a$。

a模p的阶

如果$a$不被素数$p$整除，则$a$模$p$的阶是指使得$a^e=1（mod p）$的最小指数$e>=1$。例如2、3、4、5、6模7的阶分别是3、6、3、6、2，记$Ord_p(a)$。

所以原根的也可定义：
设m是正整数，a是整数，若a模m的阶等于$\phi(m)$，则称a为模m的一个原根。假设一个数g对于P来说是原根，那么$g^i mod P,i\in[2,\phi(P))$的结果两两不同.

本原根通常与幂模有关。

性质

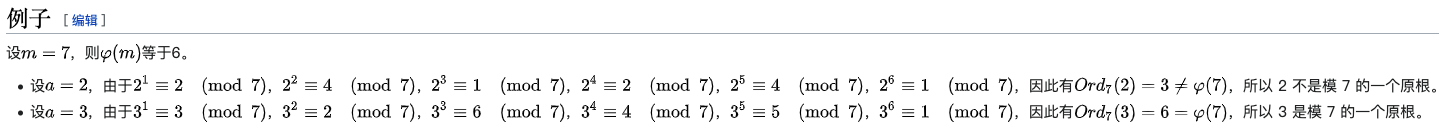
1、如果$a$是素数$p$的原根，则数$amod p,a^2 mod p,…,a^{p-1}mod p$ 是不同的并且包含$1$到$p-1$的整数的某种排列，且构成一个模$p$的简化剩余系。
2、“原根定理”：每个素数p都有本原根，而且刚好有$\phi(p−1)$个模p的本原根。

3、一个数a模p的阶$Ord_p(a)$总能整除p-1。
4、如果p有原根，则它恰有$\phi(\phi(p))$个不同的原根（无论p是否为素数都适用）
5、如果正整数${\displaystyle (a,m)=1}(a,m)=1$和正整数 d 满足${\displaystyle a^{d}\equiv 1{\pmod {m}}}a^{d}\equiv 1{\pmod {m}}$，则 ${\displaystyle Ord_{m}(a)}Ord_{m}(a) $整除 $d$。因此${\displaystyle Ord_{m}(a)}Ord_{m}(a)$整除${\displaystyle \varphi (m)}\varphi (m)$。在例子中，当${\displaystyle a=3}a=3$时，我们仅需要验证 3 的 2、3 次方模 7 的余数即可，如果其中有一个是1，则3就不是原根。

求本原根

举一个例子：求25的本原根？
即求解一个数$a$，当$m=\phi(25)$，$a^m mod 25 =1$时，则$a$就是模25的本原根。

1、求本原根的个数
个数为$\phi(\phi(25))=\phi(20)=8$，则25的本原根个数为8个。

2、求最小本原根
设2是其中的一个原根，且$\phi(25)=20$，$2^2mod25=4,...,2^5mod 25=7,...,2^{10}mod 25=24,...2^{20}mod 25=1$，最后$2^{20}mod 25$才等于1，故2是25的一个本原根。

还有一种方法检测：$2$是否是25的本原根？

验证$\phi(25)=20,20(20=2*2*5)$有两个素因子2和5，$2^2mod 25=4,2^{5}mod 25=7$，计算结果没有1，则2是25的本原根。

3、利用已知最小的本原根求其他本原根
20的简化剩余系（且与20互素且小于20的集合）是$(1,3,7,9,13,17,22,23)$，则可以由本原根2求出其他本原根：

$2^1mod25=2,2^3mod25=8,2^7mod 25=22,2^9mod 25=12,2^{11}mod 25=23,2^{13}mod 25=17,2^{17}mod 25=22,2^{19}mod25=13$

所以25的本原根为$(2,3,8,12,13,17,22,23)$。

或者是逐个判断从[2,25)之间的数$a$，只有$a^{m}mod25=1$，当且仅有$m=\phi(25)=20$时，$a$才是25的本原根。

程序实现

1、计算25的本原根（逐个计算）

#-*-coding:utf-8-*-

'''
求出25的所有本原根
'''

#与25互素的所有数的集合封装于List ：primeList中
primeList = [1 , 2 , 3 , 4 , 6 , 7 , 8 , 9 , 11 , 12 , 13 , 14 , 16 , 17 , 18 , 19 , 21 , 22 , 23 , 24]

byg = []    #用于存储25的本原根List ：byg
list = []    #用于存储遍历primeList中元素测试结果的集合

for j in primeList :    #对所有与25互素的数字进行遍历测试
    for i in range (1 , 21) :    #求出每个数字的1-20次方并mod 25
        list.append (j**i % 25)
    list.sort()            #将集合list进行排序
    if primeList == list :    #比较集合是否与primeList相同，若相同此时的j为25的本原根
        byg.append (j)    #将本原根j压入byg中
    else :
        pass    #否则，不执行任何操作
    list = []    #初始化list ， 以备下一次迭代

print ("25的所有本原根为 ： " , byg)    #将25的所有本原根组成的集合byg打印出来

或者为：
（1）在计算25的所有本原根时，首先我们要得到25的欧拉函数值可以知道25=5^2，其欧拉函数值=25-5=20，且这20个数为1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19,21,22,23,24。
（2）接着遍历这些数依次求解这些数的1-20次方对25取余，并且这20个数不重复，且均在这些数里，编程里体现为对求得的20个数排序再比较。
（3）由于高次幂会溢出，参考了大数计算优化的快速幂取余算法解决了这个问题。

#include<iostream>
using namespace std;

void bubbleSort(int arr[], int n);//冒泡排序
int power(long int x, long int y, long int n);//快速幂取余实现(x^y%n)

int main()
{
	int i,j,k,flag[20];
	int n=25,sum=20;
	int s[20]={1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19,21,22,23,24}; 
	cout<<"25的所有本原根为：";
	for(i=0;i<sum;i++)
	{
		k=0;
		for(j=1;j<sum+1;j++)
		{
			//这里要利用快速幂取余，否则数值太大会溢出
			flag[j-1]=power(s[i],j,n);
		}
		bubbleSort(flag,sum);
		
		for(j=0;j<sum;j++)
		{
			if(flag[j]!=s[j])
				k=1;
		}
		if(k==0)
			cout<<s[i]<<" ";
	}
	cout<<endl<<endl;
	return 0;
}

//冒泡排序
void bubbleSort(int arr[], int n)
{
	for(int i = 0;i < n;i++)
	{  
		for(int j = 0;j < n-i-1;j++)
		{  
            if(arr[j] > arr[j+1])
			{  
                int t = arr[j];  
                arr[j] = arr[j+1];  
                arr[j+1] = t;  
            }  
        }  
    }       
}
//快速幂取余实现(x^y%n)
int power(long int x, long int y, long int n)
{
	long int t = 1;
	while (y > 0)
	{
		if (y % 2 == 1)
		{
			y -= 1;
			t = t*x%n;
		} else {
			y /= 2;
			x = x*x%n;
		}
	}
	return t%n;
}

2、求p的本原根个数

#include<iostream>
#include <cmath>
using namespace std;

/*
 * 求模p的本原根数
 */
int euler(int x)
{
    int res = x;
    for(int i=2;i<(int)sqrt(x*1.0)+1;i++)
    {
        if(x%i == 0)
        {
            res = res/i*(i-1);
            while(x%i==0)
                x/=i;
        }
    }
    if(x>1)res = res/x*(x-1);
    return res;
}

int main()
{
    int p=25;
    cout << euler(p-1);

    return 0;
}

3、求大素数的本原根

#includestdio.h
#includestdlib.h
#include "miracl.h"
#include time.h
time_t begin, end;
int main()
{
	int MAX_D=0;
	miracl* mip = mirsys(MAX_D + 10, 10);
	big p = mirvar(0);
	big p_1 = mirvar(0);//p-1
	big p_2 = mirvar(0);//p-2
	big q = mirvar(0);
	big g = mirvar(0);

	big flag = mirvar(0);//中间变量
	big one = mirvar(1);//常量1

	printf("----------------------------\n\n");
	printf("        素数生成元\n\n");
	printf("----------------------------\n\n");
	printf("请输入生成素数的位数：");
	scanf("%d", &amp;MAX_D);
	//密钥生成部分
	{
		irand((unsigned)time(NULL)); // 使用当前时间作为随机数种子 
		//随机生成一个安全素数p
		bigdig(MAX_D, 10, q);//生成一个150位的随机数
		nxsafeprime(0, 0, q, p);//生成一个比q大的安全素数p
		copy(p, q);
		decr(q, 1, q);
		subdiv(q, 2, q);//生成q=(p-1)/2
		decr(p, 1, p_1);//生成p_1=p-1
		decr(p, 2, p_2);//生成p_2=p-2
		//寻找一个本原根
		//irand((unsigned)time(NULL)); // 使用当前时间作为随机数种子 
		while (1)
		{
			bigrand(p_1, g);//g小于p-1
			if (compare(g, one) = 0)//保证g大于1
				continue;
			powmod(g, mirvar(2), p, flag);
			if (compare(flag, one) != 0)
			{
				powmod(g, q, p, flag);
				if (compare(flag, one) != 0)
				{
					multiply(q, mirvar(2), flag);
					powmod(g, flag, p, flag);
					if (compare(flag, one) == 0)
						break;
				}

			}
		}//end
		printf("p = ");
		cotnum(p, stdout);
		printf("g = ");
		cotnum(g, stdout);
	}
	mirexit();
	system("pause");
	return 0;
}

参考

1、https://blog.csdn.net/xdu_truth/article/details/8093029
2、https://blog.csdn.net/weixin_40520963/article/details/86685657

上一篇：黑灰产眼中的NFT：平台嗷嗷待宰，用户送钱上门
下一篇：没有了

求本原根

相关文章