绪论与算法基础 1️⃣ 定义 :如果存在两个正常数 \(c\) 和 \(n_0\) ,对于所有的 \(n \ge n_0\) ,有 \(|f(n)| \le c|g(n)|\) ,则记作 \(f(n)=O(g(n))\)
1️⃣ 定义:如果存在两个正常数 \(c\) 和 \(n_0\) ,对于所有的 \(n \ge n_0\) ,有 \(|f(n)| \le c|g(n)|\) ,则记作 \(f(n)=O(g(n))\)
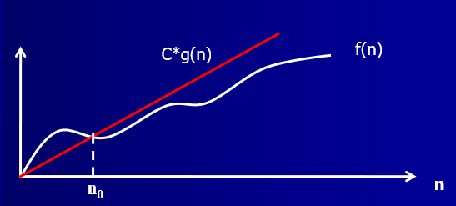
1️⃣ 定义:如果存在两个正常数 \(c\) 和 \(n_0\) ,对于所有的 \(n \ge n_0\) ,有 \(|f(n)| \le c|g(n)|\) ,则记作 \(f(n)=O(g(n))\)
