由《算法导论》的描述,堆的本质是一个完全N叉树,它以数组作为元素的存储载体。这里注意和“堆内存”的概念做区分。
一个二叉堆的结构如下图所示。包括堆的逻辑结构(A)和存储结构(B):
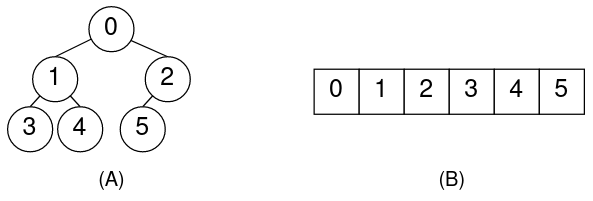
树通常以指针来构建节点间的连接关系,而堆是利用数组的下标关系来构建树状结构。下标为i的元素,它的左右孩子分别是下标为2*i+1和2*i+2的元素(如果下标从0开始)。这也使得构建出的树是一个完全二叉树。
本文针对它的逻辑结构(完全N叉树)进行研究,对树和堆同样适用。
关于最大堆如果一个堆的所有节点的值都大于等于其孩子(如果有的话),则称之为最大堆或大根堆。或者说,如果堆的所有“父子三元组”中父节点都是最大者,则此堆为最大堆。如下图所示:
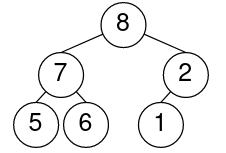
显然,整个堆的最大值就是其根元素。最小堆的原理类似。
最大堆的相关操作堆维护了一个元素的集合。一个集合常见的操作包括:“增删改查建”。我们按难易程度分别做表述。
- 查询节点:我们可以查询堆的最大值
- 改变节点:我们可以改变任何一个节点的值
- 删除节点:我们只考虑删除一个叶子节点的情况
- 插入节点:我们只考虑插入一个叶子节点的情况
- 建立堆:我们可以从某个集合中建立最大堆
堆的根节点即为最大值节点。查询的时间复杂度为O(1)。
改变节点的值改变某个节点的值可能会破坏最大堆的性质,需要进行调整使之重新恢复为最大堆。如果节点新值大于旧值,则进行向上调整;反之进行向下调整。调整规则为:
- 向上调整:如果当前节点大于其父节点,则与之交换;迭代这个过程直至根节点或无需交换为止。
- 向下调整:如果当前节点小于其“最大的子节点”,则与之交换;迭代这个过程直至叶节点或无需交换为止。
示例如下:
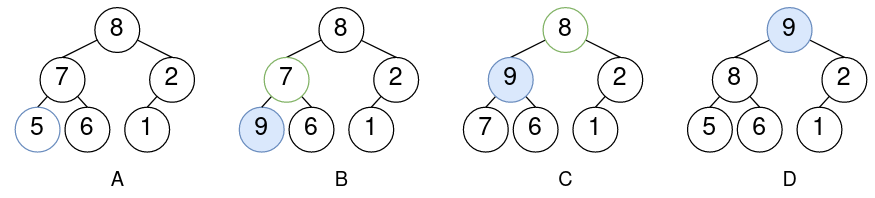
以上为向上调整的示意图。改堆A的元素5为9,得到堆B。发现9大于其父节点7,因而与之交换得到堆C。此时发现9大于其父节点8,因而交换得到堆D。此时至根节点,操作结束。
向下调整也是一样,注意调整时是与其“最大的子节点”进行交换:
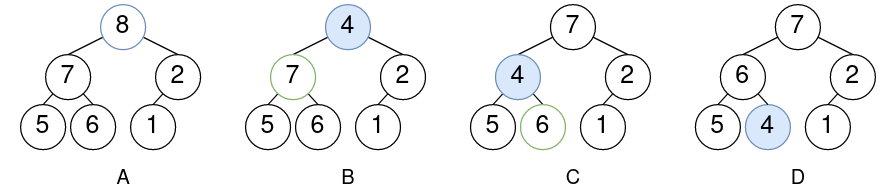
改堆A的元素8为4,得到堆B。4的孩子中最大者为7,4小于7故与之交换得到堆C。此时4的孩子中最大者为6,4小于6故与之交换得到堆D。此时至也节点,操作结束。
时间复杂度:无论是向上或向下调整,至多调整h步则至根节点或叶节点,h是堆的深度,约为log(N)。因此时间复杂度为log(N)。
插入和删除叶子节点我们回到最大堆的定义:堆的所有节点的值都大于等于它的孩子(如果有)。那么如果某个节点缺少左孩子或右孩子,我们姑且认为它有一个值为无穷小的左孩子或右孩子。因此插入叶子节点,则可认为是改大了某个无穷小的节点;删除叶子节点,则可认为是改小了某个节点。此时,可对应地使用向上或向下调整。
值得注意的是,如果执行的是删除节点,被删节点本身是叶节点,所以无需向下调整。
时间复杂度:插入为log(N),删除为O(1)。
建堆已知一个数组,用其中的元素建立一个最大堆。容易想到的方法就是初始化一个空堆,然后依次从数组中取出元素插入到堆中。这样的时间复杂度为O(NlogN),因为单单它的叶节点就约N/2个,每个需要调整约logN次。关于完全二叉树的叶子节点数问题,参考这里。
更快的方法是,用数组直接构建一个堆,然后调整它成为最大堆。过程是自底至顶,逐层对每个元素进行向下调整。叶子节点因为本身就在堆底,所以不用调整。
例如:
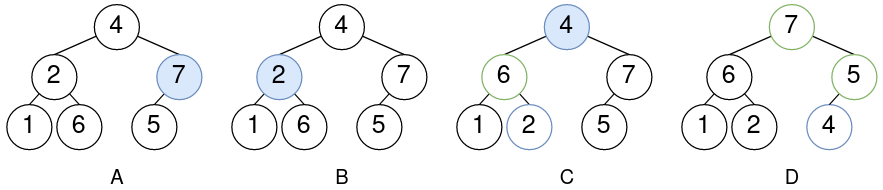
假设已知堆A,调整过程为:
- 叶子节点(1,6,5),不需要调整。
- 倒数第二层我们去调整2和7。因为对它们的调整互不影响,所以无所谓顺序。对7调整后得到堆B,没有实质变化。对2调整后得到堆C。
- 调整最高层节点(4),得到堆D。
时间复杂度:除叶节点外,至多调整N/2个节点,每次调整需要log(N)次,似乎时间复杂度为NlogN。但实际上不是的:
数量为N的完全二叉树中,叶节点约有N/2个,高度为0,不需调整;其父节点约N/4个,高度为1,需调整1次;后者的父节点约N/8个,高度为2,需调整2次; …… 最后根节点只有一个,高度为logN-1, 需调整logN-1次:
\[T = \frac{N}{2^1} * 0 + \frac{N}{2^2} * 1 + \frac{N}{2^3} * 2 + \frac{N}{2^4} * 3 + ... + \frac{N}{2^{logN}} * (logN-1) \]等号两边同乘以2,得到
\[2T = N * 0 + \frac{N}{2^1} *1 + \frac{N}{2^2} * 2 + \frac{N}{2^3} * 3 + ... + \frac{N}{2^{logN-1}} * (logN-1) \]后式减去前式(错位相减,后式第i个元素减去前式中第i-1个元素),则:
\[T = \frac{N}{2^1} + \frac{N}{2^2} + \frac{N}{2^3} + ... - \frac{N}{2^{logN}} * (logN-1) \]最后一项等于logN-1,前面的是等比数列,其和为N。因此T约等于\(N-logN+1\)。所以时间复杂度是O(N)。
证明 向上调整下面证明增大最大堆的某个元素后,向上调整会得到一个最大堆。
我们可以提出一个条件不变式:堆在每一步调整前后,以当前节点为根的子堆T1,和堆中剩下的部分T2,两者均为最大堆。这里的最大堆可以是非完全的。
我们给出一个示例,如下图所示。我们把堆A中的节点c增大至c',得到堆B。此时整个堆分为两部分:以c'为根的子堆T1(图示蓝色部分)和其他的部分T2(图示绿色部分)。
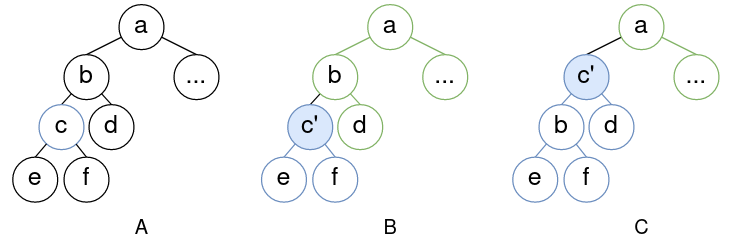
T1在改动前后,它的根从c增至c',因此依然是个最大堆。T2在改动前后没有变化,所以也是最大堆。
如果c'<=b,不需调整,此时显然为最大堆。如果c'>b,则交换c'和b,得到堆C。此时得到以c'为根的子树T1'(图示蓝色部分)和其他部分T2'(图示绿色部分)。接下来证明它们满足条件不变式。
从B到C的过程中,T2'是T2的一部分,所以自然是最大堆。我们关注堆C中的T1':
- 对于c'-b-d这个三元组:由于在B中c'>b>=d,因此c'是c'-b-d中最大者
- 对于b-e-f这个三元组:由于在B中b>=e且b>=f,因此b是b-e-f中最大者
- T1中其他三元组没有发生变化
因此T1'的所有三元组中,父节点均为最大者,所以T1'是最大堆。
因此得证,每次迭代都满足条件不变式。如果迭代结束,要么当前节点为整个堆的根,要么它不再大于其父,都易得当前堆为最大堆。
向下调整下面证明减小最大堆的某个元素后,向下调整会得到一个最大堆。这里的最大堆可以是非完全的。
我们可以提出一个条件不变式:当前节点与其孩子节点的连线把整个堆分为三个子堆T1、T2和T3,三者均为最大堆。
如下图所示,减小堆A的节点b至b',得到B,此时b'与孩子c和d的连线把整个堆分为三个子堆:以c为根的子堆T2(图红色部分)和以d为根的子堆T3(图绿色部分)和其他部分(图蓝色部分)。当然,如果a没有左孩子或右孩子,则相应部分为空。
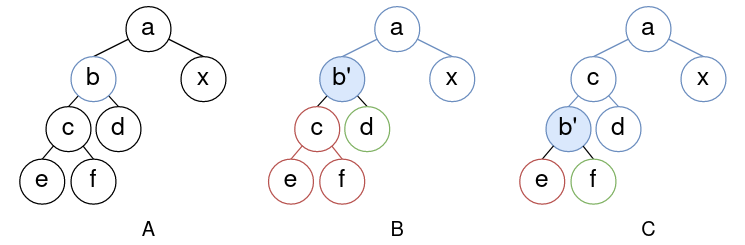
从A到B的过程中,T2和T3没有发生变化,依然是最大堆;T1减小了一个叶节点b,依然是最大堆。
假设b'的孩子中最大的是c(即c>=d)。如果此时b'>=c,则不需调整,易得当前依然是最大堆。如果b'<c,则交换b'和c得到堆C。此时得到新的子树T1', T2', T3'。
T2'和T3'分别是T2和T3的一部分,自然也是最大堆;我们关注堆C中T1':
- 对于三元组a-b-x来说,因为在B中a>=c且a>=x,所以a是a-c-x中最大者
- 对于三元组c-b'-d来说,因为在B中b'<c且c>=d,所以c是c-b'-d中最大者
- T1中其他的三元组不受影响
所以,T1'是最大堆,满足不变式。
因此每次迭代前后都满足不变式。如果迭代结束,要么当前节点为叶子节点,要么它不再小于其孩子,均易得当前堆为最大堆。
建堆对于建堆过程中的证明可以简化为求证这样一个问题:
已知一个堆中,某个节点的左右两个子树都是最大堆,那么从这个节点向下调整后,以这个节点位置为根的子树是最大堆。如图,a节点的两个子树都是最大堆,求证从a开始向下调整后,会得到一个最大堆。
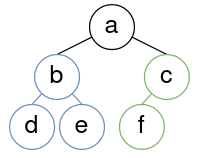
这里用一个新思路来理解:假设a节点的值是无穷大,那么当前显然是最大堆;如果然后改小了a的值变成了现在的情况,那么从根向下调整自然可以恢复为最大堆。
建堆的时候是从底到顶调整节点。在调整节点a时,其子树都是最大堆。那么调整后,以a原位置为根的堆是最大堆。迭代完成后,最终会得到一个整体的最大堆。
最大堆的应用 优先队列最大堆可用于构建优先队列。优先队列的操作包括:
- 查询最大值:返回堆顶元素
- 插入新元素:在堆底第一个可用位置插入元素,向上调整
- 弹出最大值:返回堆顶元素;删除堆底最末元素,改堆顶元素为它的值,向下调整。如图所示:
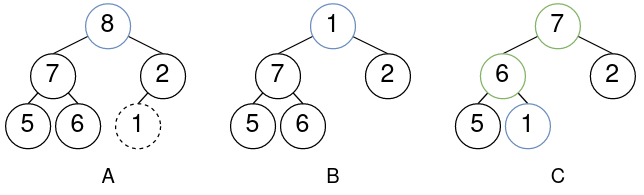
弹出最大值的操作也可以等效为:交换堆顶和堆底最末元素的值;移除最末元素;从堆顶向下调整。
堆排序堆排序的步骤为:
- 用数组(a,b,c,...)构建出最大堆。
- 每次迭代执行:交换堆顶和堆底最末元素的值;移除最末元素;从堆顶向下调整。这和优先队列的弹出最大值操作一致。
我们在上文谈到,堆的存储载体是数组。它在移除最末元素时,会缩减载体数组的规模。如图所示:
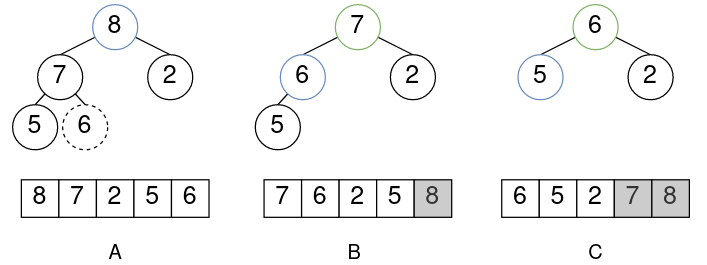
我们从数组的角度来看迭代过程。数组整体上分为两部分:最大堆的载体部分和余下部分。每次迭代时,最大堆会把自己最大的元素放到尾部,然后失去它,它便成为了余下部分的头部元素。
最终,最大堆的载体数组会越来越短,只留下余下部分。前者每次都失去它的最大元素,而后者每次都接受前者的最大值作为头部元素,因此它是有序的。迭代完成后,便得到一个有序数组。
