目录 OpenCV库（一） 一、 简介 1、 简介 2、 环境配置 2.1 第一种 2.2 第二种 3、 运行原理 3.1 灰度图像数字化 3.2 色彩深度和色阶 3.3 彩色图像数字化 二、 基本操作 1、 图像IO操作 1.1 读取
- OpenCV库（一）
- 一、 简介
- 1、 简介
- 2、 环境配置
- 2.1 第一种
- 2.2 第二种
- 3、 运行原理
- 3.1 灰度图像数字化
- 3.2 色彩深度和色阶
- 3.3 彩色图像数字化
- 二、 基本操作
- 1、 图像IO操作
- 1.1 读取图像
- 1.2 显示图像
- 1.3 保存图像
- 2、 绘制几何图形
- 2.1 绘制直线
- 2.2 绘制圆形
- 2.3 绘制矩形
- 2.4 添加文字
- 2.5 效果展示
- 3、 操作图片
- 3.1 修改像素点
- 3.2 获取图像属性
- 3.3 拆分合并
- 3.4 色道改变
- 4、 算术操作
- 4.1 图像加法
- 4.2 图像混合
- 4.3 图像位运算
- 1、 图像IO操作
- 三、 滤波器
- 1、 卷积
- 1.1 什么是图片卷积
- 1.2 padding
- 1.3 卷积核大小
- 1.4 卷积语法
- 2、 滤波器
- 2.1 方盒滤波和均值滤波
- 2.2 高斯滤波
- 2.3 中值滤波
- 2.4 双边滤波
- 3、 算子
- 3.1 索贝尔算子
- 3.2 沙尔算子
- 3.3 拉普拉斯算子
- 1、 卷积
- 一、 简介
Opencv（Open Source Computer Vision Library）是一个基于开源发行的跨平台计算机视觉库，它实现了图像处理和计算机视觉方面的很多通用算法，已成为计算机视觉领域最有力的研究工具。在这里我们要区分两个概念：图像处理和计算机视觉的区别：图像处理侧重于“处理”图像–如增强，还原，去噪，分割等等；而计算机视觉重点在于使用计算机来模拟人的视觉，因此模拟才是计算机视觉领域的最终目标
图是物体反射或透射光的分布，像是人的视觉系统所接受的图在人脑中所形成的印象或认识
OpenCV用C++语言编写，它具有C ++，Python，Java和MATLAB接口，并支持Windows，Linux，Android和Mac OS， 如今也提供对于C#、Ch、Ruby，GO的支持
2、 环境配置 2.1 第一种下载OpenCV：【https://www.lfd.uci.edu/~gohlke/pythonlibs/#opencv】
找到对应版本的OpenCV，下载下来
复制文件的地址：【"D:\Documents\opencv_python-4.5.5-cp39-cp39-win_amd64.whl"】
然后打开终端输入：【pip install "D:\Documents\opencv_python-4.5.5-cp39-cp39-win_amd64.whl"】
安装完成后
创建一个python文件，在文件中输入
import cv2
print(cv2.__version__)
2.2 第二种成功运行代表安装成功
直接在终端输入：pip install opencv-python
这种方式安装较慢哦！
注意：运行OpenCV还要有依赖库 numpy
安装 numpy
pip install numpy
3、 运行原理
一般的图像（模拟图像）不能直接用计算机来处理，必须先将图像转化为数字图像。把模拟图像分割成一个个像素，每个像素的亮度或灰度值用一个整数表示——图像的数字化
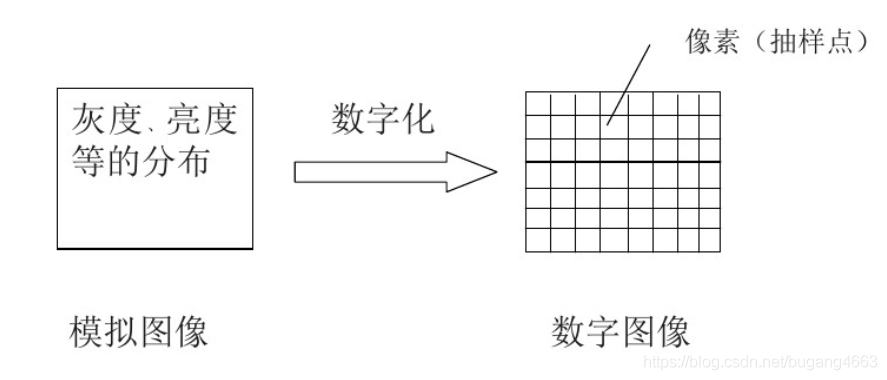3.1 灰度图像数字化
所谓的数字化，其实就是化成同行同列的二维数组，而每个坐标存的就是相关的灰度值（0-255）(为什么是0-255？一个字节存放8bit，而图的储存一般都是以uint8类型存放，同时计算机时按照二进制存放数值，也就是2的8次方，也就是256）
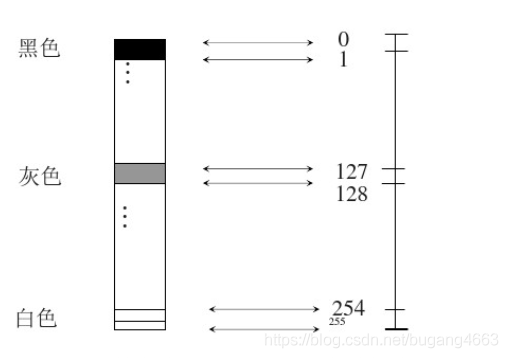3.2 色彩深度和色阶
彩色像数字化原理同灰度图像数字化，只不过彩色图像为三通道图像且可以拆分成三张同等像素的灰度图，由下图可知，每三个BGR就组成了一张图片的一列
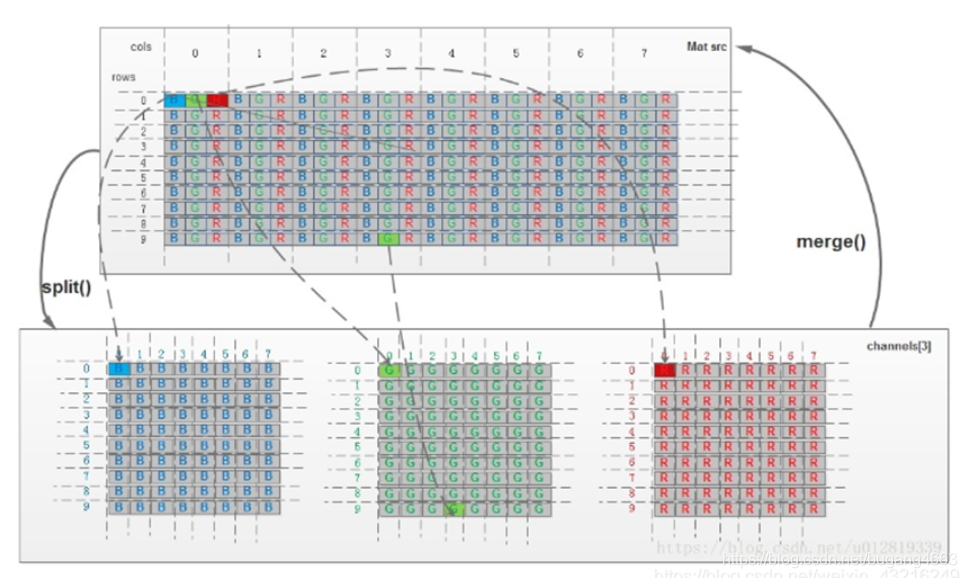
数字图像处理的实质就是通过对数字图像中像素数据的判断，依据处理或识别要求，最后逐个像素修改像素的灰度值
二、 基本操作学习目标：
- 掌握图像的读取和保存方法
- 能够使用OpenCV在图像上绘制几何图像
- 能够访问图像的像素
- 能够获取图像的属性，并进行通道的分离和合并
- 能够实现颜色空间的变换
1、 图像IO操作 1.1 读取图像
语法：cv2.imread(path, mode)
参数：
path：要读取的图像mode：读取方式的标志-
cv2.IMREAD_COLOR\1：以彩色模式加载图像，任何图像的透明度都将忽略，这个默认参数 -
cv2.IMREAD_GRAYSCALE\0：以灰度模式加载图像 -
cv2.IMREAD_UNCHANGED\-1：包括alpha通道的加载图像模式注意：
- 可以使用数字代替这些标志，数字在源码中可以查看
-
实例：
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo01.py"
__time__ = "2022/7/15 19:30"
import cv2.cv2 as cv2
img = cv2.imread("./img/1.jpg", 0) # 以灰度模式读取图像
cv2.imshow("image", img)
cv2.waitKey(0)
1.2 显示图像如果图像读取错误，其不会报错，而是会使图像为空值
语法：cv2.imshow(winname, mat)
参数：
winname：显示图像窗口名称，以字符串类型显示mat：要加载的图像
要注意：在调用显示图像API后，要调用
cv2.waitKey()给绘制图像留下时间，否则窗口会出现无响应的情况，并且图像无法显示出来
另外，我们也可以使用matplotlib对图像进行展示
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo01.py"
__time__ = "2022/7/15 19:30"
import cv2.cv2 as cv2
from matplotlib import pyplot as plt
img = cv2.imread("./img/1.jpg")
cv2.imshow("image", img)
cv2.waitKey(0) # 0代表等待足够的时间
cv2.destroyAllWindows() # 摧毁窗口
# 使用matplotlib显示图片
plt.imshow(img[:, :, ::-1]) # 将rgb转换为bgr，数组逆置
# 灰度图的读取模式：plt.imshow(img, cmap=plt.cm.gray)
plt.show()
语法：cv2.imwrite(fielname, img)
参数：
filename：文件名，路径img：要保存的图像
代码：
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo01.py"
__time__ = "2022/7/15 19:30"
import cv2.cv2 as cv2
import numpy as np
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray) # 声明图像数据为numpy的数组
cv2.imwrite("test.jpg", img)
语法：cv2.line(img, start, end, color, thickness)
参数：
img：要绘制直线的图像Start, End：起始点、终点color：直线的颜色thickness：线条的宽度，为-1时生成闭合图案，并填充颜色
语法：cv2.circle(img, centerpoint, r, color, thickness)
参数：
centerpiont：圆形的坐标r：圆的半径- 其它参数和绘制直线的参数意义相同
语法：cv2.rectangle(img, leftupper, rightdown, color, thickness)
参数：
leftupper：矩形左上角坐标rightdown：矩形右下角坐标
语法：cv2.putText(img, text, station, font, fontsize, color, thickness, cv.Line_AA)
参数：
station：文本放置位置text：要写入的文本数据font：字体fontsize：字体大小
我们生成一个全黑的图像，然后再里面绘制图像并添加文字
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo02.py"
__time__ = "2022/7/15 21:36"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
# 创建一个空白的图像 1920x1080
img = np.zeros([1080, 1920, 3], np.uint8) # 并且设置数据类型为uint8
# 绘制图形
cv2.line(img, (0, 0), (502, 502), (255, 255, 255), 4)
cv2.rectangle(img, (502, 502), (900, 900), (255, 0, 0), 4)
cv2.circle(img, (800, 700), 100, (0, 255, 0), 4)
# 写入文字
cv2.putText(img, "hello world", (10, 500), cv2.FONT_HERSHEY_COMPLEX_SMALL, 4, (255, 255, 0), 4) # 使用cv2内置的字体
plt.imshow(img[:, :, ::-1]) # 逆置图像
plt.title("test")
plt.show()
我们可以通过行和列的坐标值获取像素值，对于RGB图像，它返回一个rgb的数组，对于灰度图像，仅返回相应的强度值，使用相同的方法对像素值进行修改
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo02.py"
__time__ = "2022/7/15 21:36"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread("./img/1.jpg")
# 声明img的类型
assert isinstance(img, np.ndarray)
# 获取对应点的像素强度值
print(img[100, 200])
# 修改某个点的像素值
img[100, 100] = [255, 255, 255]
plt.imshow(img[:, :, ::-1])
plt.show()
图像属性包括行数、列数和通道，图像数据类型，像素值等
img.shape
图像大小
img.size
数据类型
img.dtype
3.3 拆分合并
有时需要在B、G、R通道图像上单独工作。在这种情况下，需要将BGR图像分割为单个通道，或者在其他情况下，可能需要将这些单独的通道合并到BGR图像，你可以通过以下方式完成：
# 通道分离
b, g, r = cv2.split(img)
# 通道合并
img = cv2.merge(b, g, r)
实例：
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo02.py"
__time__ = "2022/7/15 21:36"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray)
plt.imshow(img[:, :, ::-1]) # 进行色道的逆置，转换为bgr
b, g, r = cv2.split(img) # 分离
plt.imshow(b, cmap=plt.cm.gray)
plt.show()
img2 = cv2.merge((b, g, r)) # 返回rgb图像
plt.imshow(img2[:, :, ::-1])
plt.show()
OpenCV中有150多种颜色空间转换方法，最广泛的转换方法有两种，BGR->Gray和BGR->HSV
语法：cv2.cvtColor(input_image, flag)
参数：
input_image：进行颜色空间转换的图像flag：转换类型cv2.COLOR_BGR2GRAY：BGR->GRAYcv2.COLOR_BGR2HSV：BGR->HSV
学习目标：
- 了解图像的加法，混合操作
你可以使用OpenCV的cv2.add()函数把两幅图像相加，或者可以简单通过numpy操作添加两个图像，如：res = img1 + img2，两个图像应该具有相同大小和类型，或者第二个图像可以是标量值
注意：OpenCV加法和Numpy加法之间存在差异，OpenCV的加法的饱和操作，而Numpy添加时模运算操作
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "logic.py"
__time__ = "2022/7/16 10:52"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
x = np.uint8([250])
y = np.uint8([10]) # unsigned int-8
print(cv2.add(x, y)) # 250 + 10 = 260 -> 255
print(x + y) # 250 + 10 = 260 % 256 = 4
# 实例
# 导入图像
img1 = cv2.imread("./img/1.jpg")
assert isinstance(img1, np.ndarray)
img2 = cv2.imread("./img/2.jpg")
assert isinstance(img2, np.ndarray)
# 对图像进行相加
img3 = cv2.add(img1, img2)
plt.imshow(img3[:, :, ::-1])
plt.show()
img4 = img1 + img2
plt.imshow(img4[:, :, ::-1])
plt.show()
4.2 图像混合推荐使用OpenCV里面的加法
cv2.add()和减法cv2.subtract()
图像混合其实也是加法，但是不同的是两幅图像的权重不同，这就会给人一种混合或者透明的感觉，图像混合的计算公式如下：
\(g(x)=(1-\alpha) \cdot f_0(x) + \alpha \cdot f(x)\)
通过修改阿尔法的值，可以实现非常酷的操作
现在我们把两幅图混合在一起，第一幅图的权重是0.7，第二幅图的权重是0.3，函数cv2.addWeight(img1, alpha, img2, beta, gamma)可以按下面公式对图片进行混合操作
\(dst = \alpha \cdot img_1 + \beta \cdot img_2 + \gamma\)
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "logic.py"
__time__ = "2022/7/16 10:52"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
img1 = cv2.imread("./img/1.jpg")
assert isinstance(img1, np.ndarray)
img2 = cv2.imread("./img/2.jpg")
assert isinstance(img2, np.ndarray)
img3 = cv2.addWeighted(img1, 0.7, img2, 0.3, 0) # 根据权重混合
plt.imshow(img3[:, :, ::-1])
plt.show()
OpenCV的逻辑运算——与、或、非、异或
OpenCV中的非：0 反过来是 255
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo9.py"
__time__ = "2022/7/18 18:09"
import cv2.cv2 as cv2
import numpy as np
# 读取图像
img = cv2.imread("./img/1.jpg") # 读取黑白效果
assert isinstance(img, np.ndarray)
img_ = np.zeros(img.shape, np.uint8)
# 非操作
img_not = cv2.bitwise_not(img)
# 或操作
img_or = cv2.bitwise_or(img, img_)
# 与操作
img_and = cv2.bitwise_and(img, img_)
# 展示图片
cv2.namedWindow("not", cv2.WINDOW_NORMAL)
cv2.resizeWindow("not", 640, 480)
cv2.imshow("not", np.hstack((img[:640, :480], img_not[:640, :480])))
cv2.namedWindow("and", cv2.WINDOW_NORMAL)
cv2.resizeWindow("and", 640, 480)
cv2.imshow("and", np.hstack((img[:640, :480], img_and[:640, :480])))
cv2.namedWindow("or", cv2.WINDOW_NORMAL)
cv2.resizeWindow("or", 640, 480)
cv2.imshow("or", np.hstack((img[:640, :480], img_or[:640, :480])))
cv2.waitKey(0)
cv2.destroyAllWindows()
图像卷积就是卷积核在图像上按行滑动遍历像素时不断在相乘求和的过程
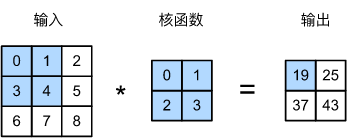
基本概念
-
步长
步长就是卷积核在图像上移动的步幅，卷积核可以每次移动一个像素步长或者两个像素步长等
步长一般为1
-
padding
从上面图片中，我们可以看出，卷积之后图片的长宽会变小，如果要保持图片大小不变。我们需要在原始图片周围填充0。padding指的就是填充0的圈数。
我们如何判断需要补0的圈数呢？
我们可以通过公式计算出需要填充的0的圈数：
-
输入体积大小：\(H_1 \cdot W_1 \cdot D_1\)
-
四个超参数：
- Filter数量K
- Filter大小F
- 步长S
- 零填充大小P
-
输出体积大小：\(H_2 \cdot W_2 \cdot D_2\)
\[\begin{matrix} H_2 = (H_1 - F + 2P) / S + 1\\ W_2 = (W_1 - F + 2P) / S + 1 \\ D_2 = K \end{matrix} \]3 x 3 的卷积核 结果 -2 5 x 5 的卷积核 结果 -4 7 x 7 的卷积核 结果 -6 -
求圈数：
\((H_1 - F + 2P) / S + 1 = H_1\)
通过这个式子可以求出补0的圈数
如果步长为1，则可以推导出\(P=\frac{F-1}{2}\)
1.3 卷积核大小图片卷积中，卷积核一般为奇数，比如 3 x 3，5 x 5，7 x 7。为什么一般是奇数呢？
- 根据上面padding的计算 公式，如果要保持图片大小不变，采用偶数卷积核的话，将会出现奇数圈0的情况
- 奇数维度的过滤有中心，便于指出过滤器的位置，即OpenCV卷积中的锚点
语法：cv2.filter2D(src, ddepth, kernel, [, dest[, anchor[, delta[, borderType]]]])
参数：
ddpeth：其为卷积之后图像的位深，即卷积之后图片的数据类型，一般为-1，表示和原图类型一致kernel：卷积和大小，用元组或者ndarray表示，要求数据类型必须是float32类型anchor：锚点，即卷积核的中心点，是可选参数，默认是(-1, -1)delta：可选参数，表示卷积之后额外加一个值，相当于线性方程中的偏差，默认是0borderType：边界类型，一般不设
案例：
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo04.py"
__time__ = "2022/7/17 9:52"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
img = cv2.imread("./img/1.jpg", cv2.IMREAD_GRAYSCALE) # 读取灰度图
assert isinstance(img, np.ndarray)
# 创建核结构，kernel必须是float32类型
kernel = np.array([
[-1, -1, -1],
[-1, 8, -1],
[-1, -1, -1]
], np.float32) # 轮廓效果
# 进行卷积
img_ = cv2.filter2D(img, -1, kernel)
# 图片展示
cv2.namedWindow("img", cv2.WINDOW_NORMAL)
cv2.resizeWindow("img", 1920, 1080)
cv2.imshow("img", img_)
cv2.waitKey(0)
cv2.destroyAllWindows()
2、 滤波器 2.1 方盒滤波和均值滤波卷积核可以在网上查找
方盒滤波
语法：cv2.boxFilter(src, ddepth, ksize[, dist[, anchor[, normalize[, borderType]]]])
方盒滤波的卷积核形式如下：
\[K = a\begin{bmatrix} 1 & 1 & \cdots& 1\\ 1& 1 &\cdots & 1 \\ \cdots &\cdots &\cdots &\cdots\\ 1& 1 &\cdots & 1 \end{bmatrix} \]参数：
nomalize：- 其为True时，\(a=\frac{1}{W \cdot H}\)
- 其为False时，a = 1
- 一般情况下，我们都使用
nomalize=True的情况，这时，方盒滤波等价于均值滤波 ksize：卷积核大小
均值滤波
语法：cv2.blur(src, ksize[, dest[, anchor[, borderType]]])
代码演示：
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo04.py"
__time__ = "2022/7/17 9:52"
import cv2.cv2 as cv2
import numpy as np
# 读取图像
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray)
# 使用滤波器
img_ = cv2.boxFilter(img, -1, (5, 5), normalize=True) # 模糊处理
img_1 = cv2.blur(img, (5, 5)) # 模糊处理
# 图片展示
cv2.namedWindow("img", cv2.WINDOW_NORMAL)
cv2.resizeWindow("img", 1920, 1080)
cv2.imshow("img", img_)
cv2.waitKey(0)
cv2.destroyAllWindows()
要理解高斯滤波，首先要知道什么是高斯函数，高斯函数是在符合高斯分布（也叫正态分布）的数据的概率密度函数
高斯函数的特点：以x轴某一点（这一点称为均值）为对称轴，越靠近中心数据发生的概率越高，最终形成一个两边平缓，中间陡峭的钟型图形
高斯函数的一般形式为：
一维高斯分布：\(G(x)=\frac{1}{\sqrt{2\pi \sigma}}e^{-\frac{(x-\mu)^2}{2\sigma ^2}}\)
二维高斯分布：\(G(x, y)=\frac{1}{\sqrt{2\pi \sigma ^ 2}}e^{-\frac{x^2 + y^2}{2\sigma ^2}}\)
高斯滤波就是使用符合高斯分布的卷积核对图片进行卷积操作，所以高斯滤波的重点就是如何计算符合高斯分布的卷积核，即高斯模板
通过高斯函数计算出来的是概率密度函数，所以我们还要确保这九个点加起来为1，我们需要将这九个点求和，再分别求权重，得到最终的高斯模板
语法：cv2.GaussianBlur(src, ksize, sigmaX[, dist[, sigmaY[, borderType]]])
参数：
ksize：高斯核的大小sigmaX：X轴的标准差sigmaY：Y轴的标准差，默认为0，这时：sigmaX = sigmaY- 如果指定sigma值为0，会分别从ksize的宽度和高度中计算sigma
选择不同的sigma值会得到不同的平滑效果，sigma越大，平滑效果越明显
高斯滤波可以去除噪点
2.3 中值滤波中值滤波原理非常简单，假设有一个数组，取其中的中间值（即中位数）作为卷积后的结果值即可，中值滤波对胡椒噪点效果明显
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo04.py"
__time__ = "2022/7/17 9:52"
import cv2.cv2 as cv2
import numpy as np
# 读取图像
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray)
# 使用滤波器
img_ = cv2.medianBlur(img, 5) #注意，中值滤波这里的ksize就是一个数字
# 图片展示
cv2.namedWindow("img", cv2.WINDOW_NORMAL)
cv2.resizeWindow("img", 1920, 1080)
cv2.imshow("img", img_)
cv2.waitKey(0)
cv2.destroyAllWindows()
双边滤波对于图像的边缘信息能够更好的保存，其原理为一个与空间距离相关的高斯函数与一个灰度距离相关的高斯函数相乘
-
空间距离：指的是当前点与中心点的欧式距离。空间域高斯函数其数学形式为：
\[e^{-\frac{(x_i-x_c)^2 + (y_i - y_c)^2}{2\sigma ^2}} \]其中，(\(x_i\), \(y_i\))为当前位置，(\(x_c\), \(y_c\))为中心点的位置，sigma为空间域标准差
-
灰度距离：指的是当前点灰度与中心点灰度的差的绝对值，值域高斯函数其数学形式为：
\[e^{-\frac{(gray(x_i, y_i) -gray(x_c, y_c))^2}{2\sigma ^2}} \]
双边滤波本质上是高斯滤波，双边滤波和高斯滤波不同的是：双边滤波既利用了位置信息，又利用了像素信息来定义滤波窗口的权重，而高斯滤波只利用了位置信息
双边滤波中加入了对灰度信息的权重，即在邻域内，灰度值越接近中心点灰度值权重更大，灰度值相差大的权重点权重越小，此权重大小，则有高斯函数确定
两者权重系数相乘，得到最终的卷积模板，由于双边滤波需要每个中心点邻域的灰度信息来确定其系数，所以其速度比一般滤波慢得多，而且计算量增长速度为核大小的平方
双边滤波可以保留边缘，同时可以对边缘内的区域进行平滑处理，相当于做了美颜
语法：bilateralFilter(src, ksize, sigmaColor, sigmaSpace[, dst[, borderType]])
参数：
ksize：卷积核大小，传入数字sigmaColor：计算像素信息使用的sigmasigmaSpace：计算空间信息使用的sigma
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo04.py"
__time__ = "2022/7/17 9:52"
import cv2.cv2 as cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray)
# 使用滤波器
img_ = cv2.bilateralFilter(img, 7, 20, 50)
# 图片展示
cv2.namedWindow("img", cv2.WINDOW_NORMAL)
cv2.resizeWindow("img", 640, 480)
cv2.imshow("img", img_)
cv2.waitKey(0)
cv2.destroyAllWindows()
边缘是像素值发生跃迁的位置，是图像的显著特征之一，在图像特征提取，对象检测，模式识别等方面都有重要作用
人眼如何识别图像边缘？
比如有一副图，图里面有一条线，左边很亮，右边很暗，那人眼就很容易识别这条线作为边缘，也就是像素的灰度值快速变化的地方
3.1 索贝尔算子索贝尔算子对图像求一阶导数，一阶导数越大，说明像素在该方向作为边缘，也就是像素灰度值快速变换的地方
因为图像的灰度值都是离散的数字，索贝尔算子采用离散差分算子计算图像像素点亮度值的近似梯度
图像是二维的，即沿着宽度/高度这两个方向
我们可以得到两个新的矩阵，分别反映了每一点像素在水平方向上的亮度变化情况和在垂直方向上的亮度变换情况
综合考虑这两个方向的拜年话，我们可以使用平方和相加的方式\(G=\sqrt{G_x^2 + G_y^2}\)反映某个像素的梯度变化情况，有时候为了简单起见，也直接使用绝对值相加替代\(G=|G_x|+|G_y|\)
语法：Sobel(src, ddepth, dx, dy, dst=None, ksize=None, scale=None, delta=None, borderType=None)
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo5.py"
__time__ = "2022/7/18 11:20"
import cv2.cv2 as cv2
import numpy as np
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray)
# 注意sobel算子要分开计算x，y的梯度女
# 计算X轴方向的梯度
dx = cv2.Sobel(img, -1, 1, 0, None, 3)
# 计算Y轴方向的梯度
dy = cv2.Sobel(img, -1, 0, 1, None, 3)
# 计算和梯度
img_ = cv2.add(dx, dy)
cv2.namedWindow("img", cv2.WINDOW_AUTOSIZE)
# cv2.imshow("img", dx)
# cv2.imshow("img", dy)
cv2.imshow("img", np.hstack((img_, dx, dy)))
cv2.waitKey(0)
cv2.destroyAllWindows()
当内核大小为3时，以上的索贝尔内核可能产生比较明显的误差（其值求取了导数的近似值）
为了解决这一问题，OpenCV提供了Scharr函数，但该函数仅作用于大小为三的内核，该函数的运算与索贝尔函数一样快，但是结果更加精确
沙尔算子和索贝尔算子很类似，只不过使用不同的内核值，放大了像素变换的情况
语法：Scharr(src, ddepth, dx, dy, dst=None, scale=None, delta=None, borderType=None)
# ！/usr/bin/python3
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo5.py"
__time__ = "2022/7/18 11:20"
import cv2.cv2 as cv2
import numpy as np
img = cv2.imread("./img/1.jpg")
assert isinstance(img, np.ndarray)
# 注意sobel算子要分开计算x，y的梯度女
# 计算X轴方向的梯度
dx = cv2.Scharr(img, -1, 1, 0)
# 计算Y轴方向的梯度
dy = cv2.Scharr(img, -1, 0, 1)
# 计算和梯度
img_ = cv2.add(dx, dy)
cv2.namedWindow("img", cv2.WINDOW_AUTOSIZE)
# cv2.imshow("img", dx)
# cv2.imshow("img", dy)
cv2.imshow("img", np.hstack((img_, dx, dy)))
cv2.waitKey(0)
cv2.destroyAllWindows()
索贝尔算子是模拟一阶求导，导数越大的地方说明变换越剧烈，越有可能是边缘，那么如果继续对导数求导呢？可以发现边缘处的二阶导数为0，我们可以利用这一特性去寻找图像的边缘（二阶导数为0的位置也可能是无意义的位置）
拉普拉斯算子推导过程：
以x方向求解为例：
\[ {matrix} 一阶差分：f^{'}x = f(x) - f(x-1)\\ 二阶差分：f^{"}(x) = f^{'}(x+1) - f^{'}(x)=(f(x+1) - f(x))-((f(x) - f(x-1))\\ 化简后：f^{"}(x) = f(x-1)-2f(x)+f(x+1)\\ 同理可得：f^{"}(y) = f(y-1)-2f(y)+f(y+1)\\ 把x, y方向的梯度叠加到一起：\\ f^{"}(x, y) = f^{"}_x(x, y)+f^{"}_y(x, y)\\ =f(x-1, y)+f(x+1, y) + f(x, y-1) + f(x, y+1)-4f(x, y)\\ 这个等式可以用矩阵写成：\\ f^{"}(x, y) = \begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{bmatrix} \odot \begin{bmatrix} f(x-1, y-1)&f(x, y-1)&f(x+1, y-1)\\ f(x-1, y)&f(x,y)&f(x+1, y)\\ f(x-1, y+1)&f(x, y+1)&f(x+1, y+1) \end{bmatrix}\\ 这样就得到了拉普拉斯算子的卷积核即卷积模板 $$ {matrix} 语法：`cv2.Laplacian(src, ddepth, dst=None, ksize=None, scale=None, delta=None, borderType=None)` 可以同时求两个方向的边缘 对噪音敏感，需要先进行去噪，再调用拉普拉斯算子 ```python # ！/usr/bin/python3 # -*- coding: UTF-8 -*- __author__ = "A.L.Kun" __file__ = "demo5.py" __time__ = "2022/7/18 11:20" import cv2.cv2 as cv2 import numpy as np img = cv2.imread("./img/1.jpg") assert isinstance(img, np.ndarray) img = cv2.medianBlur(img, 7) # 进行去噪 # 计算梯度 img_ = cv2.Laplacian(img, cv2.CV_64F) # 设置位深 cv2.namedWindow("img", cv2.WINDOW_AUTOSIZE) # cv2.imshow("img", dx) # cv2.imshow("img", dy) cv2.imshow("img", np.hstack((img_, dx, dy))) cv2.waitKey(0) cv2.destroyAllWindows() ``` #### 3.4 Canny 边缘检测 Canny 边缘检测算法是用来进行多级边缘检测算法，也被很多人认为是边缘检测的最优算法，最优边缘检测的三个主要评价标准是： - 低错误率：标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报 - 高定位性：标识出的边缘要与图像中的实际边缘尽可能接近 - 最小响应：图像中的边缘只能标识一次 Canny边缘检测的一般步骤： - 去噪，边缘检测容易受到噪声影响，在进行边缘检测前通常需要先进行去噪，一般用高斯滤波去除噪声 - 计算梯度：对平滑后的图像采用sobel算子计算梯度和方向 - $G=\sqrt{G_x^2+G_y^2}$，为了方便一般可以改用绝对值相加 - $\theta =\arctan {(\frac{G_y}{G_x} )}$ - 梯度的方向被归为四类，垂直、水平和两条对角线 - 非极大值抑制 - 在获取了梯度和方向后，遍历图像，去掉所有不是边界的点 - 实现方法：逐个遍历像素点，判断当前像素点周围像素点中是否具有相同方向梯度的最大值 - 滞后阈值 语法：`Canny(img, minVal, maxVal, ...)` ```python # ！/usr/bin/python3 # -*- coding: UTF-8 -*- __author__ = "A.L.Kun" __file__ = "demo5.py" __time__ = "2022/7/18 11:20" import cv2.cv2 as cv2 import numpy as np img = cv2.imread("./img/1.jpg") assert isinstance(img, np.ndarray) # 阈值越小，细节越丰富 lena1 = cv2.Canny(img, 100, 200) # 设置阈值范围 lena2 = cv2.Canny(img, 64, 128) cv2.imshow("img", np.hstack((lena1, lena2))) cv2.waitKey(0) cv2.destroyAllWindows() ``` ## 四、 图像处理 ### 1、 几何变换 学习目标 - 掌握图像的缩放、平移、旋转等 - 了解数字图像的仿射变换和透射变换 #### 1.1 图像缩放 缩放是对图像大小进行调整，即使图像放大或缩小 语法：`cv2.resize(src, dsize, fx=0, fy=0, interpolation=cv2.INTER_LINEAR)` 参数： - `src`：输入图像 - `dsize`：绝对尺寸，直接指定调整后图像的大小 - `fx, fy`：相对尺寸，将`dsize`设置为None，然后将fx和fy设置为比例因子即可 - `interpolation`：差值方法 | 差值 | 含义 | | ------------------- | ---------------------- | | `cv2.INTER_LINEAR` | 双线性插值法 | | `cv2.INTER_NEAREST` | 最近邻插值 | | `cv2.INTER_AREA` | 像素区域重采样（默认） | | `cv2.INTER_CUBIC` | 双三次插值 | #### 1.2 图像平移 图像平移将图像按照指定方向和距离，移动到相应的位置 语法：`cv2.warpAffine(img, M, dsize)` 参数： - `img`：输入图像 - `M`：2\*3移动矩阵 对于（x, y）处的像素点，要把它移动到($x + t_x$, $y + t_y$)，M矩阵应如下设置： \]\begin{bmatrix}
1 & 0 & t_x \
0& 1&t_y
\end{bmatrix}
\begin{matrix}
M = \begin{bmatrix}
A &B
\end{bmatrix}=
\begin{bmatrix}
a_{00} & a_{01} & b_0 \
a_{10} & a_{11} & b_1
\end{bmatrix}\
A = \begin{bmatrix}
a_{00} & a_{01} \
a_{10} & a_{11}
\end{bmatrix}
B = \begin{bmatrix}
a_{00} & a_{01} & b_0 \
a_{10} & a_{11} & b_1
\end{bmatrix}\
对于任意为之(x,y)，仿射变换执行如下操作：\
T_{affine} = A\begin{bmatrix}
x\y
\end{bmatrix}+B=M\begin{bmatrix}
x\y\1
\end{bmatrix}
\end{matrix}
\begin{matrix}
T =
\begin{bmatrix}
m_{11}&m_{12} & m_{13}\
m_{21}& m_{22} & m_{23}\
m_{31} & m_{32} &m_{33}
\end{bmatrix}
= \begin{bmatrix}
T_1&T_2\
T_{3}& m_{33}\
\end{bmatrix}
\end{matrix}