0018：线段树详解

先来看一道模板题：

https://www.luogu.com.cn/problem/P3372

题目描述：

已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上 k。

2.求出某区间每一个数的和。

一看是区间查询和区间更新的题，就很容易想到线段树——线段树就是用来解决区间类型的题的。

那么什么是线段树呢？假如我们把{1,5,4,2,3}存入线段树，会是这样：

 

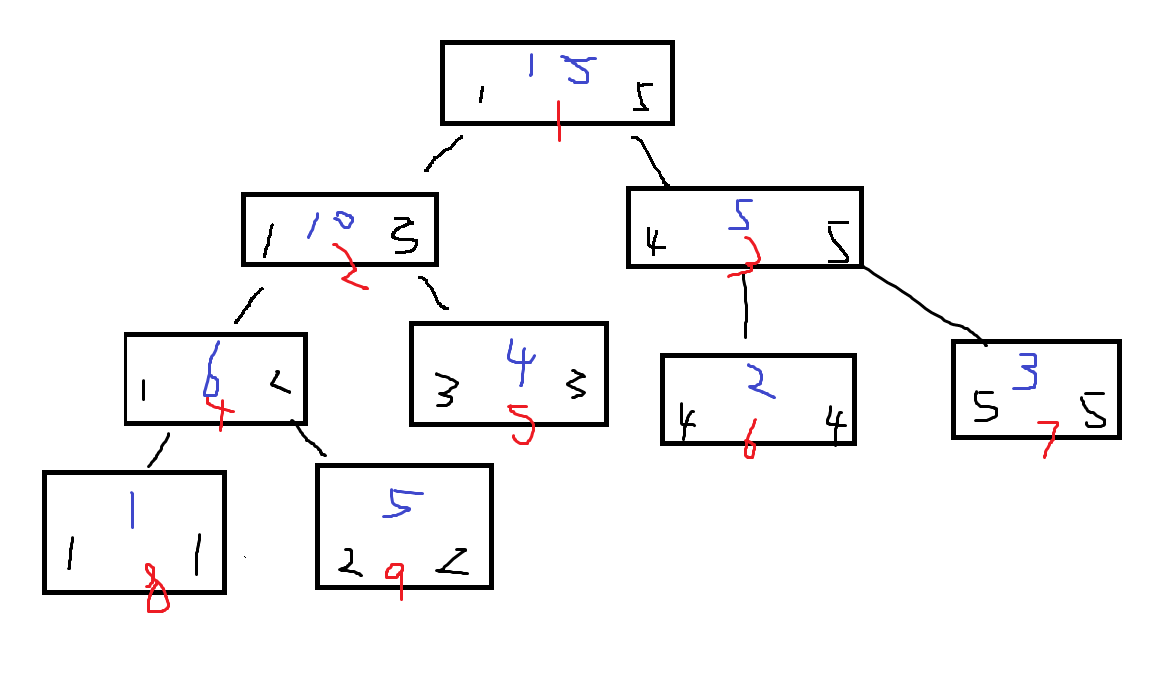
 （黑色是区间，蓝色是区间所有数的和，红色是下标）

根据这张图，不难得出：

左儿子的下标=父节点下标*2； 右儿子的下标=父节点下标*2+1

那么我们就可以以这个规律递归建树了。

 

void P(long long id){//sum是区间所有数的和 
    t[id].sum=t[id*2].sum+t[id*2+1].sum;
}
void build(long long id,long long l,long long r){//建树 
    t[id].l=l;
    t[id].r=r;//将左右端点赋值 
    if(l==r){
        t[id].sum=arr[r];
    }else{
        long long mid=(l+r)/2;//二分递归建树 
        build(id*2,l,mid);
        build(id*2+1,mid+1,r);
        P(id);//更新父节点sum值 
    }
}

 

 区间查询也基本是同理。

区间更新有点不同，那就是需要懒标记来节省时间。

就是我们更新一个父节点之后，将它打上懒标记，等到下次遍历到它的时候将他的懒标记下传，并更新子节点。

上代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 long long arr[100001];
 4 struct O{
 5     long long sum,lazy,l,r;//由于这道题数据是2^63，所以要用long long，否则只有70分 
 6 }t[400004];
 7 void P(long long id){//sum是区间所有数的和 
 8     t[id].sum=t[id*2].sum+t[id*2+1].sum;
 9 }
10 void PD(long long id){//用lazy数组进行延迟操作 
11     t[id*2].lazy+=t[id].lazy;
12     t[id*2+1].lazy+=t[id].lazy;
13     t[id*2].sum+=(t[id*2].r-t[id*2].l+1)*t[id].lazy;
14     t[id*2+1].sum+=(t[id*2+1].r-t[id*2+1].l+1)*t[id].lazy;
15     t[id].lazy=0;
16 }
17 void build(long long id,long long l,long long r){//建树 
18     t[id].l=l;
19     t[id].r=r;//将左右端点赋值 
20     if(l==r){
21         t[id].sum=arr[r];
22     }else{
23         long long mid=(l+r)/2;//二分递归建树 
24         build(id*2,l,mid);
25         build(id*2+1,mid+1,r);
26         P(id);//更新父节点sum值 
27     }
28 }
29 long long Q(long long L,long long R,long long id){//区间查询 
30     if(t[id].l>R||t[id].r<L){//如果没有重合部分，直接返回 
31         return 0;
32     }
33     if(t[id].l>=L&&t[id].r<=R){//如果当前的左右端点正好在题目给的L、R里面，返回当前节点的sum值 
34         return t[id].sum;
35     }
36     if(t[id].lazy>0){//如果lazy大于0，证明当前节点之前被lazy标记了，更新子节点的sum、lazy值并将当前节点lazy值清零 
37         PD(id);
38     }
39     return Q(L,R,id*2)+Q(L,R,id*2+1);//递归更新区间和 
40 }
41 void W(long long L,long long R,long long id,long long x){ 
42     if(t[id].l>R||t[id].r<L){
43         return;
44     }
45     if(L<=t[id].l&&R>=t[id].r){
46         t[id].sum+=(t[id].r-t[id].l+1)*x;//这里由于是求和，所以是区间长度*要加上的数 
47         t[id].lazy+=x;//lazy数组加上x 
48         return;
49     }
50     if(t[id].lazy>0){
51         PD(id);
52     }
53     W(L,R,id*2,x);
54     W(L,R,id*2+1,x);
55     P(id);//更新父节点sum值 
56 }
57 int main(){
58     int n,m,a,b,c,d;
59     cin>>n>>m; 
60     for(int i=1;i<=n;i++){
61         cin>>arr[i];
62     }
63     build(1,1,n);
64     while(m--){
65         cin>>a;
66         if(a==2){
67             cin>>b>>c;
68             cout<<Q(b,c,1)<<endl;
69         }else{
70             cin>>b>>c>>d;
71             W(b,c,1,d);
72         }
73     }
74 }

【文章转自荷兰服务器 http://www.558idc.com/helan.html 欢迎留下您的宝贵建议】