#1142 : 三分·三分求极值

描述

这一次我们就简单一点了，题目在此：

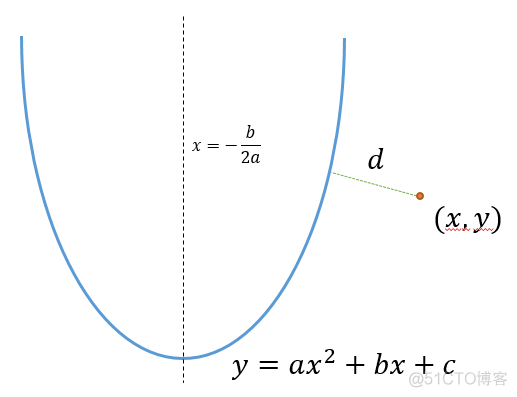
在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y)，求点P到抛物线的最短距离d。

​​提示：三分法​​

输入

第1行：5个整数a,b,c,x,y。前三个数构成抛物线的参数，后两个数x,y表示P点坐标。-200≤a,b,c,x,y≤200

输出

第1行：1个实数d，保留3位小数(四舍五入)

样例输入

2 8 2 -2 6

样例输出

2.437

三分的模板。

留下做个纪念。

代码：

#include <bits/stdc++.h>

using namespace std;
double a,b,c,x,y;
double get(double x1)
{
return sqrt((x1-x)*(x1-x)+(a*x1*x1+b*x1+c-y)*(a*x1*x1+b*x1+c-y));
}
int main()
{
scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&x,&y);
double l=-500,r=500;
double mid1,mid2,v1,v2;
while(l+1e-6<r)
{
mid1=(l+r)/2;
mid2=(mid1+r)/2;
v1=get(mid1);
v2=get(mid2);
if(v1<=v2)
{
r=mid2;
}
else
{
l=mid1;
}
}
printf("%.3lf\n",get(l));
return 0;
}