1 内容介绍
多车辆多路线的交通路线优化涉及到排序问题,是一个N-P难题,高效精确的算法存在的可能性不大.提出了基于遗传算法的求解方法,给出了实例来证明如何利用遗传算法解决多车辆多路线的优化问题.结果证明,一般情况下利用遗传算法对于多车辆多路线的行车路线优化能得到一组比较满意的解.
2 仿真代码
%fitness
%输入:种群数量,长度周转判断符,当前种群,车型,车数,点对位置,距离矩阵
%输出:fitness
function [ Chrom_ini_fitness ] = ga_fitness( PAR_ga_chrom_size,PAR_LONG_OR_UPUP,Chrom_ini,PAR_car_cap,PAR_car_kind,BASE_DATA_USING,BASE_D,PAR_car_cost)
for i=1:PAR_ga_chrom_size %PAR_ga_chrom_size输入
Chrom_this = Chrom_ini(i,:); %抽取当前一组解
[ALL_PATH,ALL_CARK,ALL_EMPT] = cun_coding_to_path_and_cark(Chrom_this,PAR_car_cap,BASE_DATA_USING); %PAR_car_cap即容积输入,BASE_DATA_USING输入
%换成路径
[ALL_LONG_UNT,ALL_UPUP_UNT] = cun_path_info( ALL_PATH,BASE_DATA_USING,BASE_D);
if size(find(cell2mat(ALL_LONG_UNT)>200),2)~=0
Chrom_this_fitness = 100000000;
else
Chrom_this_fitness = 0;
end
%计算长度及周转量
if PAR_LONG_OR_UPUP == 1 %如果是以长度为标准 %PAR_LONG_OR_UPUP输入
Chrom_this_fitness = Chrom_this_fitness + sum(cell2mat(ALL_LONG_UNT))*3.4;
ALL_CARK_NUM = cell2mat(ALL_CARK); %元胞转数值
for m=1:PAR_car_kind %输入PAR_car_kind
Chrom_car_kind = PAR_car_cap(1,m);
Chrom_car_kind_num(1,m) = size(find(ALL_CARK_NUM == Chrom_car_kind),1); %算出每种分别有多少辆
Chrom_this_fitness_add = PAR_car_cost(1,m) * Chrom_car_kind_num(1,m); %算出增加的固定成本
if m==1&&Chrom_car_kind_num(1,m)>3
Chrom_this_fitness = Chrom_this_fitness + Chrom_this_fitness_add*10000; %固定成本累加到fitness上
end
if m==2&&Chrom_car_kind_num(1,m)>3
Chrom_this_fitness = Chrom_this_fitness + Chrom_this_fitness_add*10000; %固定成本累加到fitness上
end
if m==3&&Chrom_car_kind_num(1,m)>3
Chrom_this_fitness = Chrom_this_fitness + Chrom_this_fitness_add*10000; %固定成本累加到fitness上
end
Chrom_this_fitness = Chrom_this_fitness + Chrom_this_fitness_add; %固定成本累加到fitness上
end
end
if PAR_LONG_OR_UPUP == 2 %如果是周转量
Chrom_this_fitness = sum(cell2mat(ALL_UPUP_UNT));
ALL_CARK_NUM = cell2mat(ALL_CARK); %元胞转数值
end
Chrom_ini_fitness(i,1) = Chrom_this_fitness;
end
end
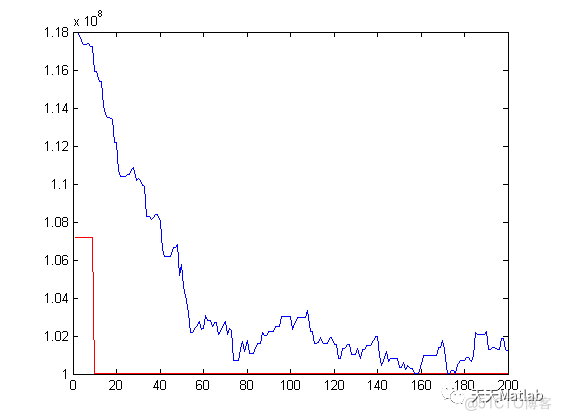
3 运行结果
4 参考文献
[1]郭鸿伟, 王娅, 郑应文. 基于遗传算法的多车辆多路线的优化方法研究[J]. 江苏电器, 2008.
[2]付春菊, 吴成东, 雷寒,等. 基于遗传算法的车辆路径规划问题研究[J]. 科技广场, 2008(10):2.
