这个题确实比较综合,也非常巧妙。 。
首先对每棵树,需要算出以每个点为根的最大深度d,这样连边的时候就能直接更新直径。。这个可以用2遍dfs上搞搞下搞搞就行。。主要维护前2大深度。。
然后如果直接统计答案的话显然是不行的。。。但是如果和起来算有个问题是可能经过这条外加边形成的直径会比原直径小,那么先和起来算之后再关注比原直径小的情况。。很容易想到的一个做法是先对d排序,求前缀和,然后枚举其中一个子树的所有节点,然后在了另一个子树上进行二分找到比原直径小的部分,然后再进行计数。。这样复杂度是O(n^2logn)虽然实际复杂度没有这么大,不过还是比较危险。。
另一个优化角度就是枚举的时候枚举比较小的树,然而这样还是能被卡,卡的方式就是将点分配到2棵树上,重复询问,因此可先离线去重后再计数。这样一来只有子树是均摊才能使这个算法的复杂度最高,设n个点平均分配在了x个树上,那么复杂度为
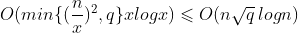
实现巨麻烦。。还考验码力就很恶心了。。。怪不得没什么人过。。
/**
* ┏┓ ┏┓
* ┏┛┗━━━━━━━┛┗━━━┓
* ┃ ┃
* ┃ ━ ┃
* ┃ > < ┃
* ┃ ┃
* ┃... ⌒ ... ┃
* ┃ ┃
* ┗━┓ ┏━┛
* ┃ ┃ Code is far away from bug with the animal protecting
* ┃ ┃ 神兽保佑,代码无bug
* ┃ ┃
* ┃ ┃
* ┃ ┃
* ┃ ┃
* ┃ ┗━━━┓
* ┃ ┣┓
* ┃ ┏┛
* ┗┓┓┏━┳┓┏┛
* ┃┫┫ ┃┫┫
* ┗┻┛ ┗┻┛
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<stdlib.h>
#include<assert.h>
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,l,r) for(int i=l;i>=r;i--)
#define link(x) for(edge *j=h[x];j;j=j->next)
#define mem(a) memset(a,0,sizeof(a))
#define ll long long
#define eps 1e-8
#define succ(x) (1<<x)
#define lowbit(x) (x&(-x))
#define sqr(x) ((x)*(x))
#define mid (x+y>>1)
#define NM 100005
#define nm 400005
#define pi 3.1415926535897931
const ll inf=1e9+7;
using namespace std;
ll read(){
ll x=0,f=1;char ch=getchar() ;
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct edge{int t;edge*next;}e[nm],*h[NM],*o=e;
void add(int x,int y){o->t=y;o->next=h[x];h[x]=o++;}
int n,m,q;
int tmp[NM][3],f[NM],len[NM],id[NM],size[NM],tot,_x,_y;
vector<int>b[NM];
vector<ll>sum[NM];
double ans[NM];
struct tmp{
int x,y,i;
bool operator<(const tmp&o)const{return size[x]<size[o.x]||(size[x]==size[o.y]&&y<o.y);}
}c[NM];
int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
void dfs1(int x){
id[x]=tot;
link(x)if(j->t!=f[x]){
f[j->t]=x;
dfs1(j->t);
if(tmp[j->t][1]+1>tmp[x][1])tmp[x][2]=tmp[x][1],tmp[x][1]=tmp[j->t][1]+1;
else if(tmp[j->t][1]+1>tmp[x][2])tmp[x][2]=tmp[j->t][1]+1;
}
}
void dfs2(int x){
b[tot].push_back(tmp[x][1]);len[tot]=max(len[tot],tmp[x][1]+tmp[x][2]);
link(x)if(j->t!=f[x]){
if(tmp[x][1]==tmp[j->t][1]+1){
if(tmp[x][2]+1>tmp[j->t][1])tmp[j->t][2]=tmp[j->t][1],tmp[j->t][1]=tmp[x][2]+1;
else if(tmp[x][2]+1>tmp[j->t][2])tmp[j->t][2]=tmp[x][2]+1;
}else{
if(tmp[x][1]+1>tmp[j->t][1])tmp[j->t][2]=tmp[j->t][1],tmp[j->t][1]=tmp[x][1]+1;
else if(tmp[x][1]+1>tmp[j->t][2])tmp[j->t][2]=tmp[x][1]+1;
}
dfs2(j->t);
}
}
int main(){
//freopen("data.in","r",stdin);
n=read();m=read();q=read();
inc(i,1,n)f[i]=i;
inc(i,1,m){
_x=read();_y=read();add(_x,_y);add(_y,_x);
int x=find(_x),y=find(_y);
f[x]=y;
}
inc(i,1,n)if(f[i]==i){
tot++;dfs1(i);
dfs2(i);size[tot]=b[tot].size();
sort(b[tot].begin(),b[tot].end());
sum[tot].push_back(b[tot][0]);
inc(j,1,size[tot]-1)sum[tot].push_back(sum[tot][j-1]+b[tot][j]);
}
inc(i,1,q){
c[i].x=id[read()];c[i].y=id[read()];c[i].i=i;
if(size[c[i].x]>size[c[i].y])swap(c[i].x,c[i].y);
}
sort(c+1,c+1+q);
inc(i,1,q)ans[i]=-1;
inc(i,1,q)if(c[i].x==c[i-1].x&&c[i].y==c[i-1].y)ans[c[i].i]=ans[c[i-1].i];
else{
int x=c[i].x,y=c[i].y;int cnt=max(len[x],len[y]);
if(x==y)continue;
ans[c[i].i]=sum[x][size[x]-1]*size[y]+sum[y][size[y]-1]*size[x]+(ll)size[x]*size[y];
for(auto&j:b[x])if(j+b[y][0]+1<cnt){
int t=lower_bound(b[y].begin(),b[y].end(),cnt-1-j)-b[y].begin();
ans[c[i].i]-=(ll)j*t+sum[y][t-1]+t;ans[c[i].i]+=(ll)t*cnt;
}
ans[c[i].i]/=size[x];ans[c[i].i]/=size[y];
}
inc(i,1,q)printf("%.8lf\n",ans[i]);
return 0;
}
D. Expected diameter of a tree
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Pasha is a good student and one of MoJaK's best friends. He always have a problem to think about. Today they had a talk about the following problem.
We have a forest (acyclic undirected graph) with n vertices and m edges. There are q queries we should answer. In each query two vertices v and u are given. Let V be the set of vertices in the connected component of the graph that contains v, and U be the set of vertices in the connected component of the graph that contains u. Let's add an edge between some vertex
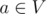
and some vertex in
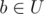
and compute the value d of the resulting component. If the resulting component is a tree, the value d is the diameter of the component, and it is equal to -1 otherwise. What is the expected value of d, if we choose vertices a and b from the sets uniformly at random?
Can you help Pasha to solve this problem?
The diameter of the component is the maximum distance among some pair of vertices in the component. The distance between two vertices is the minimum number of edges on some path between the two vertices.
Note that queries don't add edges to the initial forest.
Input
The first line contains three integers n, m and q(1 ≤ n, m, q ≤ 105) — the number of vertices, the number of edges in the graph and the number of queries.
Each of the next m lines contains two integers ui and vi (1 ≤ ui, vi ≤ n), that means there is an edge between vertices ui and vi.
It is guaranteed that the given graph is a forest.
Each of the next q lines contains two integers ui and vi (1 ≤ ui, vi ≤ n) — the vertices given in the i-th query.
Output
For each query print the expected value of d as described in the problem statement.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6. Let's assume that your answer is a, and the jury's answer is b. The checker program will consider your answer correct, if
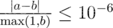
.
Examples
Input
Copy
3 1 21 33 1 2 3
Output
Copy
-12.0000000000
Input
Copy
5 2 32 44 3 4 2 4 1 2 5
Output
Copy
-12.66666666672.6666666667
Note
In the first example the vertices 1 and 3 are in the same component, so the answer for the first query is -1. For the second query there are two options to add the edge: one option is to add the edge 1 - 2, the other one is 2 - 3. In both ways the resulting diameter is 2, so the answer is 2.
In the second example the answer for the first query is obviously -1. The answer for the second query is the average of three cases: for added edges 1 - 2 or 1 - 3 the diameter is 3, and for added edge 1 - 4 the diameter is 2. Thus, the answer is
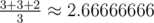
.
