1 内容介绍
随着问题规模不断增加,经典优化算法难以满足实际的需求,甚至无法得到较优解。相反,现代优化算法却表现出较好的性能,其中包括模拟退火算法(Simulatedannealing),遗传算法(Geneticalgorithm),人工神经网络算法(Neuralnetworks)[1]。“师法自然”,现代优化算法中很多都通过模拟自然界或者物理世界的现实存在来进行优化计算。20世纪90年代初由MDorigo提出的蚁群优化算法(AntColonyOptimization,ACO)是现代优化算法的一种,该算法模拟了自然界中蚂蚁的觅食行为[2]。蚁群优化算法最先被成功用于解决旅行商问题(TravelSalesmanProblem,TSP),能够有效的解决组合优化问题。和其智能算法一样,蚁群算法仍然存在着问题,包括难以平衡多样性和算法的收敛速度。进一步提高蚁群算法的性能是一个具有理论意义的问题。
自然界中,蚂蚁能够在巢穴和食物源间找到一条最优路线,并通过这条路径将食物运送回巢穴中,这样可以最少的消耗能量,有利于整个蚁群的生存。虽然单只蚂蚁的行为十分简单,但是一群蚂蚁却表现出一定的智能。著名的双桥实验验证了群体中的蚂蚁通过一种化学物质进行间接交流,该化学物质被称为信息素(pheromone),又称外激素,蚂蚁对这种信息素有一定的敏感性。每一只蚂蚁会受到其他蚂蚁信息素的影响,也会在经过的路径上释放信息素。蚂蚁在选择路径时,会更大概率的选择信息素较多的路径,这种正反馈效果使得经过的蚂蚁趋向于选择最短的路径。人们自然想到是否可以利用蚂蚁的这种特性去解决某些优化问题。自然界中,蚂蚁释放的信息素消失速度很慢,短时间内几乎不会有所减少。这种机制在有利于整个蚂蚁群体的同时,也存在另一种缺陷,如造成蚂蚁死亡旋涡现象[3]。在这种现象中,由于前面蚂蚁信息素的累积,整个蚁群跟随着一个旋涡型轨迹,持续转圈,直至最后很多蚂蚁死亡。因此,在利用蚂蚁的有利信息外,我们也必须想到如何避免某些固有的缺陷。
2 部分代码
clear;clc;
tic;
close all
%% 障碍物导入,如果起点终点设置不好,会出现错误
% load('barrier_1200x1200.mat'); goal = 1240000; start = 1;
load('barrier_reality_320.mat'); goal = 102079; start = 1;
graph = barrier;
%% 参数的设置
antNumber = 30; % 蚂蚁数目
NCmax = 200; % 最大迭代次数
rhoGlobal = 0.08; % 全局信息素挥发系数
rhoLocal = 0.1; % 局部信息素挥发系数
Beta = 1; % 启发函数式因子
Alpha = 1; % 信息素函数因子
q0 = 0.8; % 偏向选择的阈值
X = size(graph,1); % 问题的状态空间矩阵的行数
Y = size(graph,2); % 问题的状态空间矩阵的列数
tauInit = 1/((X+Y)*(X*Y));% 初始化信息素的量
tauInfo = tauInfoInit(X,Y,tauInit);
upPheromone = 500; % 信息素上限
lowPheromone = tauInit; % 信息素下限
bestSoFar_path_length = inf; % 当前最优路径长度
bestSoFar_pathNode = [];
bestSoFar_PathNode = cell(1,NCmax);
bestSoFar_PathLength = zeros(1,NCmax);
%%
for NC=1:NCmax
for k=1:antNumber
currentNode = start;
pathInfo = currentNode; % 记录一只蚂蚁的行驶路径的节点信息
path_length = 0; % 记录蚂蚁走过的路径长度
availableNode = findNextNodeSet(graph,currentNode); %% 未经过禁忌表处理的可选节点
nodeNumber = size(availableNode,1);
while(nodeNumber>0&¤tNode~=goal)
heuristicInfo = computeHeuristicInfo(goal,currentNode,graph);
tauInfo_ = tauInfo(currentNode,:)';
[info,availableNode_] = computeConvertProbability(...
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 画出栅格
axis([0,X,0,Y])
figure(1)
for i=1:X
for j=1:Y
if barrier(i,j)==1
x1=j; y1=Y-i;
x2=j; y2=Y-i+1;
x3=j-1; y3=Y-i+1;
x4=j-1; y4=Y-i;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0,0,0]);
hold on
end
end
end
%% 绘制全局最优路径节点信息
the_end_path = bestSoFar_pathNode;
the_end = length(bestSoFar_PathLength);
length_shortest = bestSoFar_PathLength(1,the_end);
len_ROUTS = length(the_end_path);
Rx = the_end_path;
Ry = the_end_path;
for i=1:len_ROUTS
Rx(i) = ( mod(the_end_path(i)-1,X) +1-0.5);
Ry(i) = ( Y- ceil(the_end_path(i)/Y) +1-0.5);
end
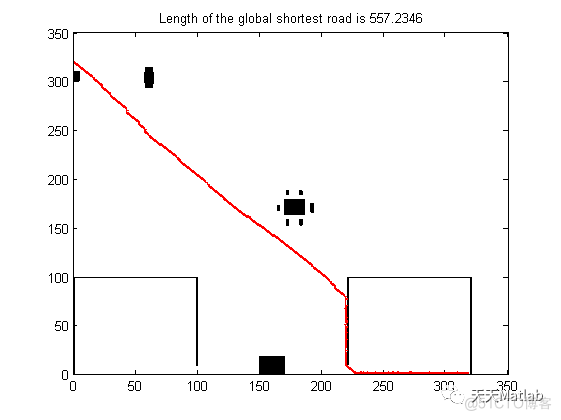
plot(Rx,Ry,'r-','lineWidth',2);% 画出最优路径图
title(['Length of the global shortest road is ',num2str(length_shortest)])
%% 绘制迭代图
figure(2)
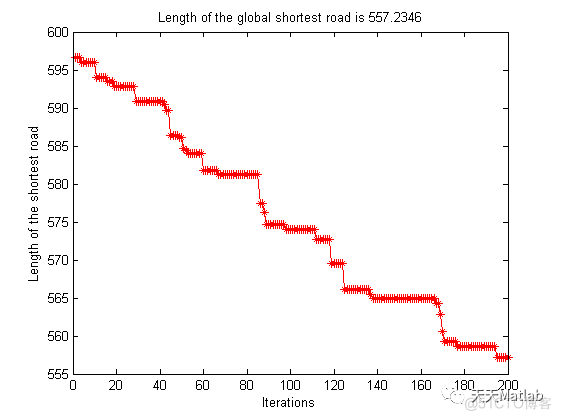
plot(bestSoFar_PathLength,'r*-')
xlabel('Iterations')
ylabel('Length of the shortest road')
title(['Length of the global shortest road is ',num2str(length_shortest)])
% %% 清除参数
% clear x X x1 x2 x3 x4 xi y Y y1 y2 y3 y3 y4 yi the_end_path the_end tauInfo_ Rx Ry i j k lehgth_shortest...
% len_ROUTS upPheromone lowPheromone
%% 保存结果和参数
% str = strcat('result_',num2str(exercise));
% save(str)
% clear str
3 运行结果
4 参考文献
[1]周东健, 张兴国, 马海波,等. 基于栅格地图-蚁群算法的机器人最优路径规划[J]. 南通大学学报:自然科学版, 2013, 12(4):91-94.
