1 内容介绍
1998年,Norden E. Huang(黄锷:中国台湾海洋学家)等人提出了经验模态分解方法,并引入了Hilbert谱的概念和Hilbert谱分析的方法,美国国家航空和宇航局(NASA)将这一方法命名为Hilbert-Huang Transform,简称HHT,即希尔伯特-黄变换。
HHT主要内容包含两部分,第一部分为经验模态分解(Empirical Mode Decomposition,简称EMD),它是由Huang提出的;第二部分为Hilbert谱分析(Hilbert Spectrum Analysis,简称HSA)。简单说来,HHT处理非平稳信号的基本过程是:首先利用EMD方法将给定的信号分解为若干固有模态函数(以Intrinsic Mode Function或IMF表示,也称作本征模态函数),这些IMF是满足一定条件的分量;然后,对每一个IMF进行Hilbert变换,得到相应的Hilbert谱,即将每个IMF表示在联合的时频域中;最后,汇总所有IMF的Hilbert谱就会得到原始信号的Hilbert谱。
2 部分代码
clear all;
close all
signal=load('Signal.txt');
N=length(signal);
fs=1840; % 采样频率
wp=[50 150]*2/fs; %对原始信号进行滤波处理
ws=[30 200]*2/fs;
rp=1;
rs=15;
[num wn]=cheb2ord(wp,ws,rp,rs);
[b,a]=cheby2(num,rs,wn);
s=filter(b,a,signal);
S=s'; % 将滤波后信号赋值给S
YSS=S; % 滤波信号为始信号
ts=(1/fs); % 采样时间
t=0:ts:ts*(N-1);
%画图---滤波后信号
figure(1)
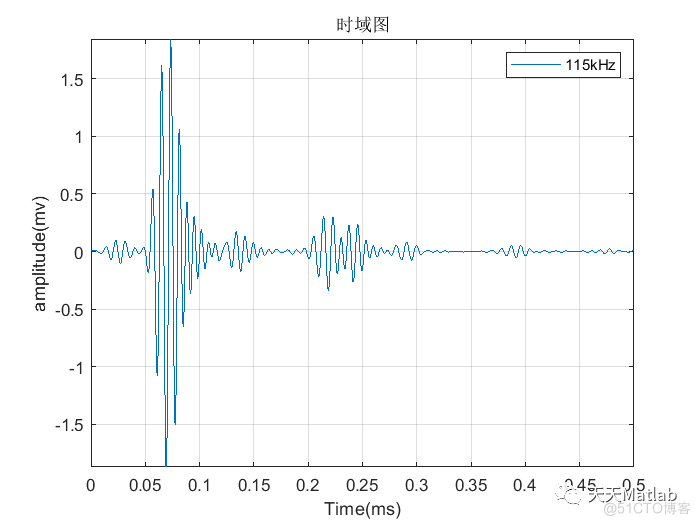
plot(t,s);
set(gcf,'color',[1,1,1]);
grid on;
xlabel('Time(ms)');
ylabel('amplitude(mv)');
title('时域图');
legend('115kHz');
axis([0,0.5,-inf,inf]);
% 设置程序中需要用到的标志位
overf=0; % 是否结束信号分解过程
overimf=0; % IMF的结束标志
%信号处理部分
SD=1; % 设置程序中需要的SD、初值
HH=0.01*ones(1,N); % 设置程序中需要的HH初值
% 进行第一次信号筛选过程
[H,overf,mline]=dob(S,t,ts); % 调用子程序
p=0; % 设置IMF组件的个数初值
% 主程序
% 第一部分:对信号进行IMF处理
condition=1;
while (overf==0) % 如果不满足信号分解结束过程
[sumnum,zeronum]=computernumber(H); % 调用子程序
SD=computerSD(H,HH); % 调用子程序
if ((zeronum==sumnum)|(abs(zeronum-sumnum)==1))&(mline(1:N)==0)
overimf=1;
condition=11;
elseif (0.2<=SD)&(SD<=0.3) % 如果H(n)满足IMF条件,退出筛选过程
overimf=1;
condition=11;
else
condition=condition+1;
end
if condition<=20
overimf=0;
else
overimf=1;
end
% 对IMF进行Hilbert处理
if overimf==1 % 如果分解值满足IMF条件
condition=1; % 重新设置condition的值,以便为下一次筛选做准备
p=p+1; % 累加IMF个数
I(p,:)=H; % 将筛选的IMF赋给I,作为第p个组件,I的每行为一个IMF
SS=YSS; % 将滤波后信号(原始信号)赋给SS
for i=1:p % 用原始信号减去所有筛选出来的IMF组件
II=I(i,:);
SS=SS-II;
end
S=SS; % 原始信号与IMF相减后的余项
% 判断余项是否可以作为最后一项信号分解组件
L=length(S);
m=0; % 以下是获得余项的导数序列
for i=1:L-1
m=m+1;
q(m)=S(i)-S(i+1); % 对余项进行求导
end
% 检查余项是否是单调或常数
if q<0 % 余项是单调递增
overf=1;
elseif q>0 % 余项是单调递减
overf=1;
elseif q==0 % 余项是恒量
overf=1;
else
overf=0;
[H,overf,mline]=dob(S,t,ts); % 不满足分解结束条件,则将余项作为原信号继续进行分解
end
else % 如果分解值不满足IMF条件,则将该分解值作为原始信号重复主程序内的步骤
S=H; % 将本次分解得到的信号作为原始信号
HH=H; % 将本次分解得到的H赋给HH,用来计算SD
[H,overf,mline]=dob(S,t,ts); % 调用子程序
end
end
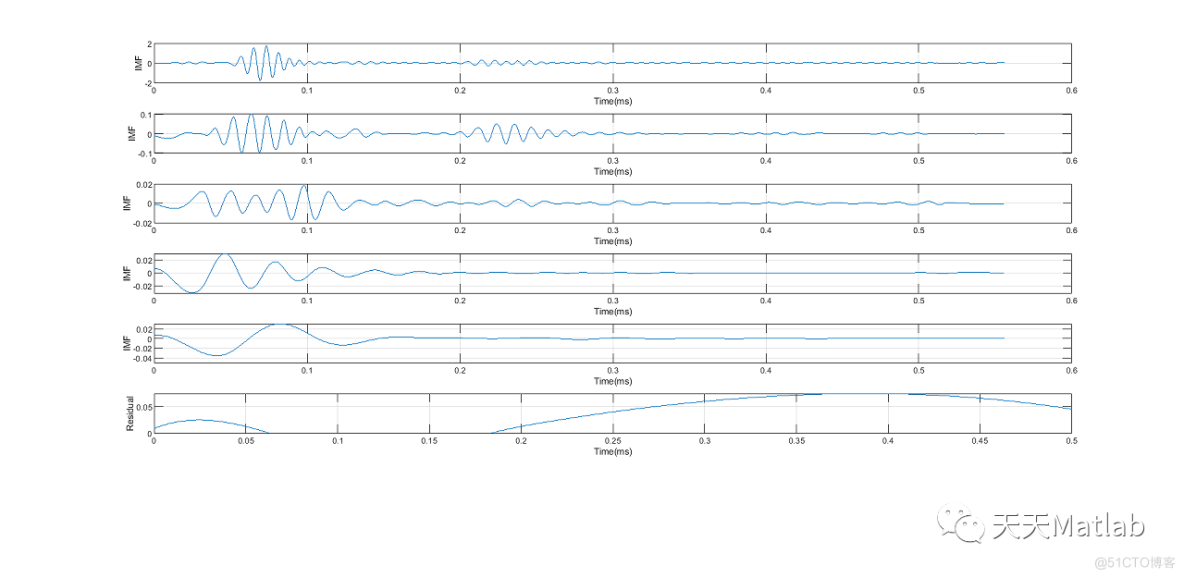
% 绘制所有IMF组件图
if p==0 % 如果信号不包括任何IMF组件
figure(2)
plot(t,H);
grid on;
xlabel('Time(ms)');
ylabel('Original Signal');
axis([0,0.5,0,inf]);
elseif (p>0) % 如果信号包括 p 个IMF组件
figure(2);
set(gcf,'color',[1 1 1]);
for i=2:p+1
subplot(p+1,1,i-1);
plot(t,I(i-1,:));
grid on;
xlabel('Time(ms)');
ylabel('IMF');
grid on;
end
xlabel('Time');
ylabel('C');
subplot(p+1,1,p);
plot(t,S);
grid on;
xlabel('Time(ms)');
ylabel('Residual');
axis([0,0.5,0,inf]);
end
% 绘制二维/三维时-频图
% 组件为p时
[w,theray,Magy,w_s,energy]=doHilbert(I,ts,t); % 调用子程序 w--原始的频率,w--p经过平滑后的频率
p=length(Magy(:,1)); % Magy的行数
q=length(Magy(1,:)); % Magy的列数
% 以下部分是获取幅值的最大值和最小值
for i=1:p
HMax(i)=Magy(i,1);
HMin(i)=Magy(i,1);
for j=2:q
if Magy(i,j)>HMax(i)
HMax(i)=Magy(i,j);
end
if Magy(i,j)<HMin(i)
HMin(i)=Magy(i,j);
end
end
end
Max=HMax(1);
Min=HMin(1);
for i=2:p
if HMax(i)>=Max
Max=HMax(i);
end
if HMin(i)<=Min
Min=HMin(i);
end
end
% 第i(0<I<=p)个组件的最大能量值和它所对应的时间值
for i=1:p
maxpoint(i)=Magy(i,1);
for j=2:1:q
if (Magy(i,j))>maxpoint(i)
maxpoint(i)=Magy(i,j)^2;
maxpoint_t(i)=t(j);
end
end
end
for i=1:q
Magy_all(i)=sum(Magy(:,i).^2);
end
maxpoint=Magy_all(1);
for i=2:1:q
if (Magy_all(i))>maxpoint
maxpoint=Magy_all(i);
maxpoint_t=t(i);
end
end
maxpoint
maxpoint_t
% 绘制二维hilbert图
% 所有组件的Hilbert图:时间-频率-fuzhi图
figure(3);
set(gcf,'color',[1 1 1]);
e1=subplot(1,1,1); % 设置句柄 e1
for i=p:-1:1
for j=1:q-1
h(i,j)=plot(t(j),w(i,j)/(2*pi)); % 绘制每个点
grid on;
%set(h(i,j),'linestyle','.');
set(h(i,j),'color',(Magy(i,j)-Min)/(Max-Min)*[1 1 1]); % 以黑色为底色,幅值越大越白
set(e1,'color',[0 0 0]); % 设置底色为黑色
hold on
end
end
hold off
xlabel('time(ms)');
ylabel('amplitude');
title('希尔波特谱图');
set(gca, 'color', 'white'); % 去掉坐标轴的背景色
set(gcf, 'color', 'white') ; % 去掉图像的背景色
axis([0 0.5 -0 300]);
% 所有组件的:时间-能量图(瞬时能量谱)
figure(4)
plot(t,Magy_all,'-');
grid on;
set(gcf,'color',[1 1 1]);
xlabel('time(ms)');
ylabel('energy');
title('瞬时能量谱');
axis([0,0.5,0,inf]);
grid on;
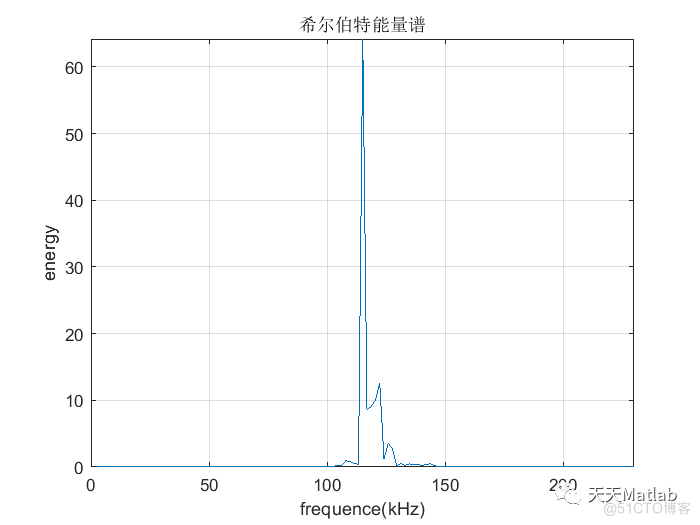
% :频率-能量图(希尔伯特谱)
e_max=energy(1); %求中心频率及其对应的最大能量
for i=2:length(w_s)
if energy(i)>e_max
e_max=energy(i);
f_c=w_s(i)/(2*pi);
end
end
e_max
f_c
figure(5)
plot(w_s/(2*pi),energy);
grid on;
hold on;
set(gcf,'color',[1 1 1]);
xlabel('frequence(kHz)');
ylabel('energy');
title('希尔伯特能量谱');
axis([0,230,0,inf]);
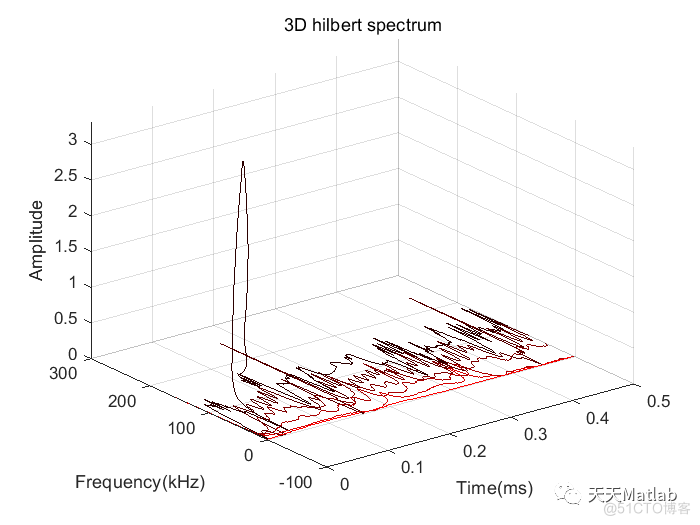
% 绘制三维的hilbert图
figure(6);
set(gcf,'color',[1 1 1]);
for i=1:p
plot3(t(1:N-1),w(i,1:N-1)/(2*pi),Magy(i,1:N-1).^2,'-','color',[1 0 0]*(i/p));
hold on
3 运行结果
4 参考文献
[1]王明阳, 柳征, 周一宇. 基于希尔波特-黄变换的冲击无线电信号检测[J]. 信号处理, 2006, 22(4):4.
