python 描述性统计

1.前言

统计分析包括描述统计Descriptive Statistics和推断统计Inferential Statistics两大部分，我们常常通过这两种方法来提取数据的一些基本特征。

备注：本文所有实现均基于已经运行import pandas as pd和import matplotlib.pyplot as plt

2.数据类型

总体来说，数据可以分为两类： 定性数据（如性别、类型）和定量数据（如温度、收益）。

3.可视化

通过可视化可以很直观的展示数据特征，最常用的是频数分布表和直方图。

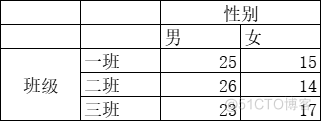
3.1频数分布表

3.2直方图

直方图是频数分布表的直观表现方式

实现方法：plt.hist("数据")

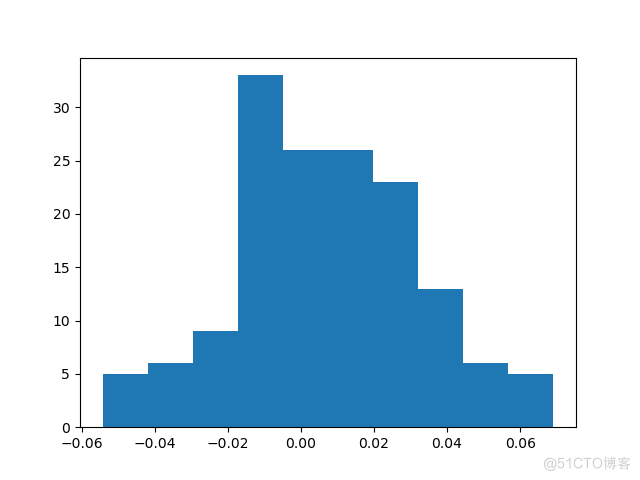可以直观的看到数据集中在0附近。

4. 数据的位置特征

位置特征 描述 算数平均数 所有数据的加和平均: $\bar{x} = \frac{x_{1}+x_{2}+...+x_{n}}{n}$ 几何平均数 所有数据的乘积开方: $\bar{x} =[\prod \limits_{i=0}^n x_i]^\frac{1}{n}$ 中位数 对于一个数据集 $x_k$，如果一个数值 $md$ 使得观测值中至少 $50%$ 数据大于等于$md$，同时至少 $50%$ 的数据小于等于 $md$ ，则md即为数据集 $x_k$中位数 众数 一组数据中出现次数最多的数值 百分位数 第 $α$ 百分分位数即为使得至少$(100-α)%$观测值大于等于该数、至少 $a%$ 观测值小于等于该数的一个数值

5. 数据的离散程度

离散特征 描述 极差 极差是指一个数据集中最大值与最小值之差，其计算公式为: 极差 =最大值一最小值 平均绝对偏差 数据偏离程度的大小: $MAD = \frac{1}{n}\sum_{i=1}^n x_i-\bar{x}$ 方差/标准差 数据与均值偏差的平方算出的用于衡量数据的离散度的指标：$\sigma^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2$ (标准差对应开根号即可 )

6. 各特征的实现方法

import numpy as np import pandas as pd # 生成100个随机数 EM_data = pd.DataFrame(np.random.random(100)) # 描述性统计 EM_data.describe() #计算算术平均数 ——使用mean函数 EM_data.mean() # 计算中位数 ——median函数 EM_data.median() # 计算众数 ——mode函数 EM_data.mode() # 计算10分位数和90分位数 ——quantile函数 [EM_data.quantile() for i in [0.1, 0.9]] # 方式二 EM_data.quantile([0.1,0.9]) # 求极差range ——max函数和min函数 EM_data.max() - EM_data.min() # 计算平均绝对偏差 ——mad函数 # 不使用mad函数求得平均绝对偏差 mad = sum([abs(x - EM_data.mean()) for x in EM_data])/len(EM_data) # 使用mad函数 EM_data.mad() # 求标准差 ——std函数 EM_data.std()