目录
- 1. matlab 中的 fmincon() 函数
- 基本语法
- 实例
- 2. python中的minimize()函数
- minimize函数的寻找参数
- minimize求解约束函数最小值
1. matlab 中的 fmincon() 函数
matlab 求解非线性规划
在matlab中,fmincon函数可以用于求解带约束的非线性多变量函数的最小值,即可以用来求解非线性规划问题。
基本语法
[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
- x 的返回值是决策向量 x 的取值,fval 的返回值是目标函数 f(x) 的取值
- fun 是用 M 文件定义的函数 f(x) ,代表了(非)线性目标函数
- x0 是 x 的初始值
- A, b, Aeq, beq 定义了线性约束 ,如果没有线性约束,则 A=[], b=[], Aeq=[], beq=[]
- lb 和 ub 是变量 x 的下界和上界,如果下界和上界没有约束,则 lb=[], ub=[],也可以写成 lb 的各分量都为 -inf, ub 的各分量都为 inf
- nonlcon 是用 M 文件定义的非线性向量函数约束。
- options 定义了优化参数,不填写表示使用 Matlab 默认的参数设置。
实例
示例,求下列非线性规划:
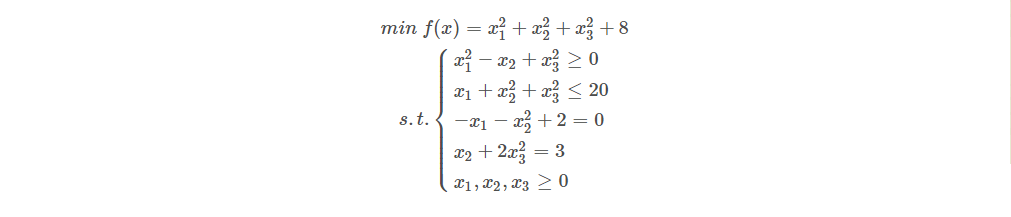
(1)编写 M 函数 fun1.m 定义目标函数:
function f = fun1(x); f = x(1).^2 + x(2).^2 + x(3).^2 + 8;
(2)编写 M 函数 fun2.m 定义非线性约束条件:
function [g, h] = fun2(x);
g = [-x(1).^2+x(2)-x(3).^2
x(1)+x(2).^2+x(3).^3-20];
h = [-x(1)-x(2).^2+2
x(2)+2*x(3).^2-3];
(3)编写主程序函数
[x, y] = fmincon('fun1', rand(3, 1), [], [], [], [], zeros(3,1), [], 'fun2')
所得结果为:

2. python中的minimize()函数
minimize函数的寻找参数
在 python 的 scipy.optimize 库中包含该函数的替代函数 minimize() ,该函数的使用与 matlab 的 fminunc 函数有些不同,下面总结下,自己在使用的过程中遇到的问题。
首先查看下该函数:
官方声明过长,我把它放在该篇博客的最后面:
# 这是其声明,我认为去查看函数的说明可以达到事半功倍的效果,千万别忽略
def minimize(fun, x0, args=(), method=None, jac=None, hess=None,
hessp=None, bounds=None, constraints=(), tol=None,
callback=None, options=None):
着重介一些重要参数代表什么:
fun:该参数就是 costFunction 你要去最小化的损失函数,将 costFunction 的名字传给 fun
官方给的提示:
The objective function to be minimized.
fun(x, *args) -> float
where x is an 1-D array with shape (n,) and args
is a tuple of the fixed parameters needed to completely
specify the function.
意思就是损失函数在定义时,**theta 必须为第一个参数且其shape必须为(n, )**即一维数组。在计算损失函数的时候用到的其他参数以元组的形式传入到 args 参数中(其他参数具体指 X,Y,lambda 等),最后返回损失的值,可以为数组形式,也可以为一个实数.
x0:参数 x0 就是初始化的 theta, 其 shape 必须为 shape(n,) 即一维数组.method:该参数代表采用的方式,默认是 BFGS, L-BFGS-B, SLSQP 中的一种,可选 TNCjac:该参数就是计算梯度的函数,和 fun 参数类似,第一个必须为 theta 且其 shape 必须为 (n, ) 即一维数组,最后返回的梯度也必须为一个一维数组。options:用来控制最大的迭代次数,以字典的形式来进行设置,例如:options={‘maxiter’:400}
minimize求解约束函数最小值
- fun: 求最小值的目标函数
- x0:变量的初始猜测值,如果有多个变量,需要给每个变量一个初始猜测值。minimize会出现局部最优的情况,所以这块的处理方法需要寻找。
- args:常数值,后面例子会讲解,fun中没有数字,都以变量的形式表示,对于常数项,需要在这里给值
- method:求极值的方法,官方文档给了很多种。一般使用默认。每种方法我理解是计算误差,反向传播的方式不同而已,这块有很大理论研究空间
- constraints:约束条件,针对fun中为参数的部分进行约束限制
1.计算 1/x+x 的最小值
# coding=utf-8
from scipy.optimize import minimize
import numpy as np
#demo 1
#计算 1/x+x 的最小值
def fun(args):
a=args
v=lambda x:a/x[0] +x[0]
return v
if __name__ == "__main__":
args = (1) #a
x0 = np.asarray((2)) # 初始猜测值
res = minimize(fun(args), x0, method='SLSQP')
print(res.fun)
print(res.success)
print(res.x)
执行结果:函数的最小值为2点多
到此这篇关于python使用minimize() 函数替代matlab的fmincon函数的文章就介绍到这了,更多相关python fmincon内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联!
