目录
前言
1 支持向量机
1.1 算法原理
1.2 超平面
1.3 几何间隔
1.4 支持向量机
1.5 凸优化问题
2 软间隔与支持向量回归
2.1 算法原理
2.2 软间隔
2.3 支持向量机
支持向量回归
前言
学习说明:预习,再看直播回放
支持向量机(3天) 预习:西瓜书6.1、6.2 直播回放:https://www.bilibili.com/video/BV1Mh411e7VU?p=8
1 支持向量机
1.1 算法原理

支持向量机和感知机都是找一个划分的超平面
感知机:找一个超平面分开
支持向量机:不近找一个超平面分开,而且是最优,其中解是唯一的
1.2 超平面
一条线,超平面就是一个点
一个面,超平面就是一条线
三维空间,超平面就是一个面

我太菜了!
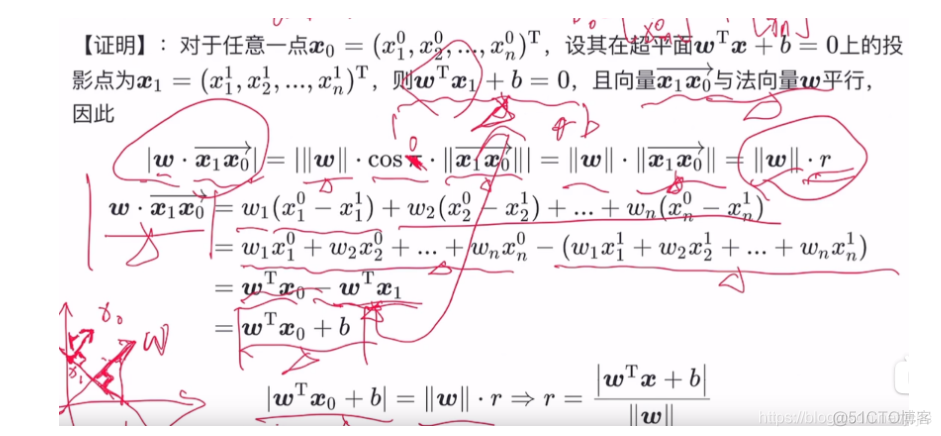
上面是up主对公式的详细证明,真不错
1.3 几何间隔

几何间隔,西瓜书中,定义wx+b>0,y为1,wx+b<0,y为-1,代入上面公式中会巧妙地得出没有正确分类时那个Y<0, 这感觉与逻辑回归中的损失函数的求解有点像

1.4 支持向量机
这里讲的是线性可分数据集X

越靠近中央的意思是 超平面越在正负样本的中央之间越大
又开始日渐复杂了

传统机器学习算法也一样重要,越感觉自己的无知


1.5 凸优化问题

对于一般地约束优化问题(不一定是凸优化问题)

拉格朗日对偶函数

我人都傻了,我是菜狗

哗啦啦 感觉好难,对偶问题,拉格朗日

<<凸优化>>这书不知道这辈子会不会拿来看一看

回到支持向量机

另外一种推到方法
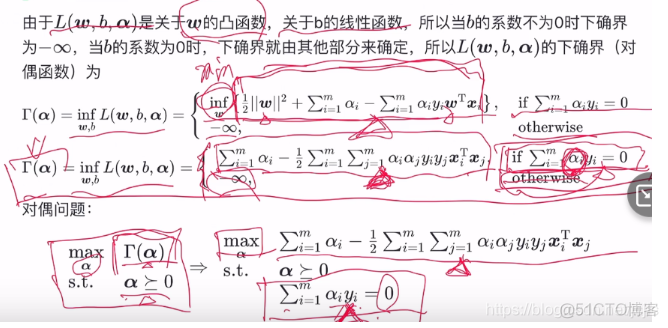
我太菜了
感觉非线性分类问题来了

当特征维数大于数据量,就是很多,sklearn里面svm文档会建议使用对偶
2 软间隔与支持向量回归
在现实任务中,线性不可分的情形才是最常见的,因此需要允许支持向量机犯错
2.1 算法原理
2.2 软间隔

2.3 支持向量机
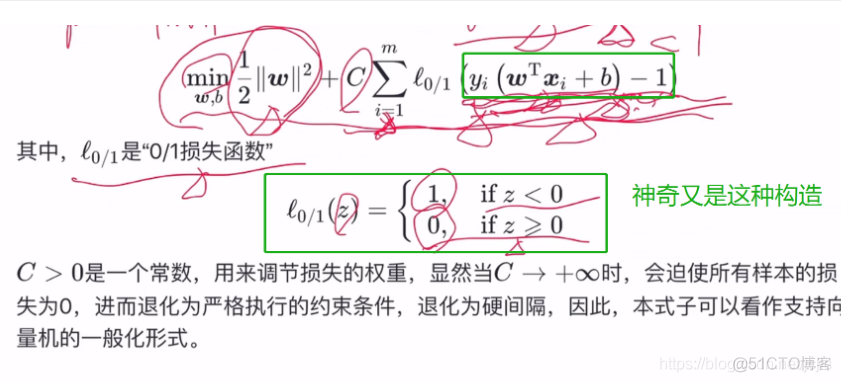
上面的C无穷大就退化为硬间隔,自己定的,超参数这个应该是,初始化模型,给用户传参,是用来调节损失的权重
做一下变换

大于1,满足。小于1,有损失,这个hinge损失函数就比前面的(0,1)损失函数好很多,是一个连续函数,凸函数,满足3个条件

数学符号真奇妙

松弛变量,允许一点犯错

允许一点越界的可能

间隔带
支持向量回归

我的天

上面是软间隔支持向量机

有点快裂开了
