目录
- 双端Diff算法
- 双端比较的原理
- 简单Diff的不足
- 双端Diff介绍
- Diff流程
- 第一次diff
- 第二次diff
- 第三次diff
- 第四次diff
- 双端Diff的优势
- 非理想情况的处理方式
- 添加新元素
- 移除不存在得节点
- 双端Diff完整代码
双端Diff算法
双端Diff在可以解决更多简单Diff算法处理不了的场景,且比简单Diff算法性能更好。本篇是以简单Diff算法的案例来展开的,不过没有了解简单Diff算法直接看双端Diff算法也是可以看明白的。
双端比较的原理
引用简单Diff算法的例子 - 案例一
oldVNode: {
type: 'div',
children: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' },
]
},
newVNode: {
type: 'div',
children: [
{ type: 'p', children: '3', key: '3' },
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' }
]
}
简单Diff的不足
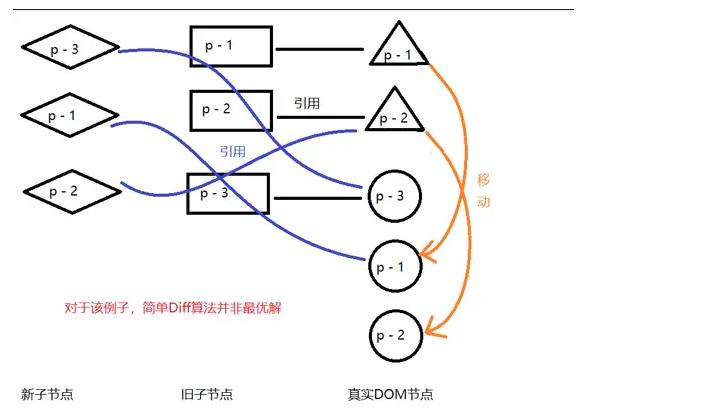
这个案例使用简单Diff算法来更新它,会发生两次DOM移动操作。然而这并不是最优解,其实只需要将 p - 3 节点移动到 p - 1 对应的真实节点前面就可以。
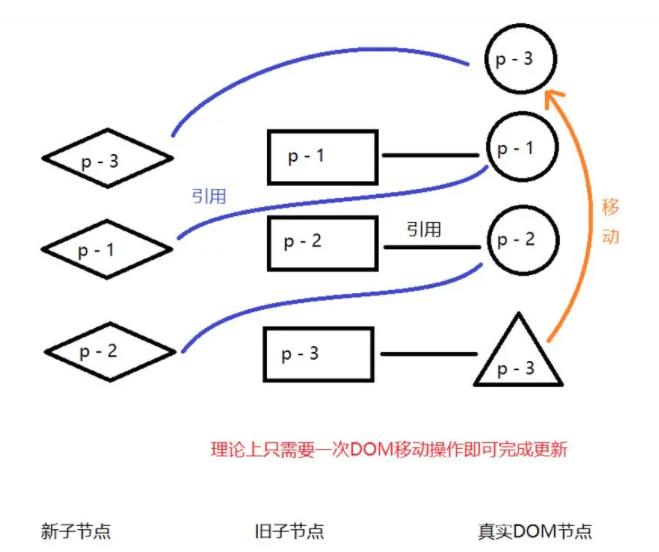
这是理论上的,简单Diff算法并不能做到这一点,要想实现还得看双端Diff算法。
双端Diff介绍
顾名思义,双端Diff算法就是同时对新旧两组子节点两个端点进行比较的算法,因此需要四个索引值指向新旧虚拟节点列表的两端。
结合该案例来看双端Diff的方式 - 案例二
newChildren: [
{ type: 'p', children: '4', key: '4' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '3', key: '3' }
],
oldChildren: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' },
{ type: 'p', children: '4', key: '4' }
]

newStartIdx / newEndIdx / oldStartIdx / oldEndIdx四个指针分别指向 新节点的第一个元素 / 新节点的最后一个元素 / 旧节点的第一个元素 / 旧节点的最后一个元素,指向的这四个元素称为 oldStartVNode / oldEndVNode / oldStartVNode / oldEndVNode。有了这些信息就可以互相比较了。
Diff流程
第一次diff
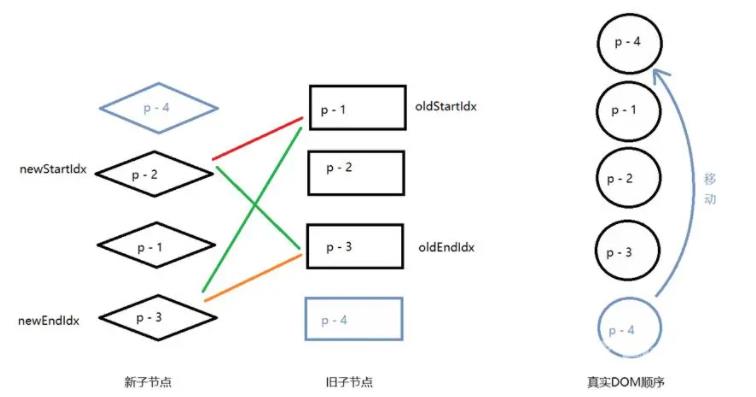
- 第一步:比较旧的一组子节点中的第一个子节点 p-1 与新的一组子节点中的第一个子节点 P-4,看看它们是否相同。由于两者的 key 值不同,因此不相同,不可复用,手是什么都不做。
- 第二步:比较旧的一组子节点中的最后一个子节点 p-4 与新的一组子节点中的最后一个子节点 p-3,看看它们是否相同。由于两者的 key 值不同,因此不相同,不可复用,于是什么都不做。
- 第三步:比较日的一组子节点中的第一个子节点 p-1与新的一组子节点中的最后一个子节点 p-3,看看它们是否相同。由于两者的 key 值不同,因此不相同,不可复用,于是什么都不做。
- 第四步:比较旧的一组子节点中的最后一个子节点 p-4 与新的一组子节点中的第一个子节点p-4。由于它们的key 值相同,因此可以进行 DOM 复用。
在第四步找到了可以复用的节点,说明它的真实DOM节点可以复用。对于可复用的节点通过移动操作即可完成更新。
那么该如何移动呢?分析下第四步比较过程的细节,第四步比较是比较旧的一组节点中的最后一个子节点 和 新的一组子节点中的第一个子节点。这说明节点 p - 4 原本是最后一个子节点,但在新的顺序中,它变成了第一个子节点。对应到代码,就是将索引 oldEndIdx 指向的虚拟节点所对应的真实DOM移动到索引 oldStartIdx 指向的虚拟节点所对应的真实DOM前面。
第一次比较完之后的情况如下:

code
第一次比较对应的代码
function insert (el, container, anchor) {
container.insertBefore(el, anchor)
}
function patchChildren (n1, n2, container) {
if (typeof n2.children === 'string') {
} else if (Array.isArray(n2.children)) {
// 到这里说明子节点都是数组类型
patchKeyedChildren(n1, n2, container)
}
}
function patchKeyedChildren (n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
// 四个端点指针
let newStartIdx = 0
let newEndIdx = newChildren.length - 1
let oldStartIdx = 0
let oldEndIdx = oldChildren.length - 1
// 四个端点元素
let newStartVNode = newChildren[newStartIdx]
let newEndVNode = newChildren[newEndIdx]
let oldStartVNode = oldChildren[oldStartIdx]
let oldEndVNode = oldChildren[oldEndIdx]
// 开始Diff
if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
// 调用patch打补丁
patch(oldEndVNode, newStartVNode, container)
// 移动DOM操作 oldEndVNode.el移动 到 oldStartVNode.el 前面
insert(oldEndVNode.el, container, oldStartVNode.el)
// 移动DOM操作完成后
oldEndVNode = oldChildren[--oldEndVNode]
newStartVNode = newChildren[++newStartVNode]
}
}
本次Diff完成之后还有其他节点需要继续进行,所以需要将diff的过程放入while循环中。满足以下情况时,说明所有节点更新完毕,因此while的条件为 oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx

第二次diff
第二次diff的情况如图
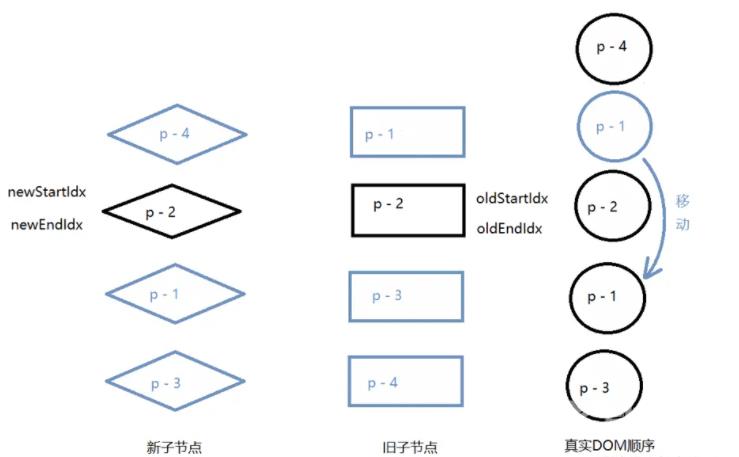
- 第一步:比较旧的一组子节点中的头部节点 p-1 与新的一组子节点中的头部节点 p-2,看看它们是否相同。由于两者的key 值不同,不可复用,所以什么都不做。(头部节点:头部素引 oldstartIdx 和 newstartIdx 所指向的节点)
- 第二步:比较1的一组子节点中的尾部节点 p-3与新的一组子节点中的尾部节点 p-3,两者的 key 值相同,可以复用。另外,由于防者都处于尾部,因此不需要对真实 DOM进行移动操作,只需要打补丁即可。
第二次diff后新旧节点的状态如下

code
第二次比较对应代码
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
// 调用patch打补丁
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
// 调用patch打补丁
patch(oldEndVNode, newStartVNode, container)
// 移动DOM操作 oldEndVNode.el移动 到 oldStartVNode.el 前面
insert(oldEndVNode.el, container, oldStartVNode.el)
// 移动DOM操作完成后
oldEndVNode = oldChildren[--oldEndVNode]
newStartVNode = newChildren[++newStartVNode]
}
}
第三次diff
第三次diff的情况如图

- 第一步:比较旧的一组子节点中的头部节点p-1 与新的组子节点的头部节点 p-2,看看它们是否相同。由于两者key值不同 不可复用,因此什么都不做。
- 第二步:比较旧的一组子节点中的尾部节点 p-2与新的一组子节点中的尾部节点 p-1看看它们是否相同,,由于两者key值不 同不可复用,因此什么都不做。
- 第三步:比较旧的一组子节点中的头部节点p-1与新的一组子节申的尾部节点p-1,两者的key 值相同,可以复用。
第三步比较中找到了相同节点,说明 p - 1 原本时头部节点,但在新的顺序中,它变成了尾部节点。因此将p - 1对应的真实DOM移动到旧的子节点的尾部节点 p - 2 对应的真实DOM后面
第三次diff后的新旧节点状态如下图
code
第三次比较对应代码
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
// 调用patch打补丁
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
patch(oldStartVNode, newEndVNode, container)
insert(oldStartVNode.el, container, newEndVNode.el.nextSibling)
oldStartVNode = oldChildren[++oldStartIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
// 调用patch打补丁
patch(oldEndVNode, newStartVNode, container)
// 移动DOM操作 oldEndVNode.el移动 到 oldStartVNode.el 前面
insert(oldEndVNode.el, container, oldStartVNode.el)
// 移动DOM操作完成后
oldEndVNode = oldChildren[--oldEndVNode]
newStartVNode = newChildren[++newStartVNode]
}
}
第四次diff
第三次diff的情况如图

第一步:比较旧的一组子节点的头部节点 p - 2 与新的一组子节点中的头部节点 p - 2。发现两者key值相同,可以复用。但两者在新旧两组子节点中都是头部节点,因此不需要移动,只需要patch函数打补丁即可。
diff结果如图
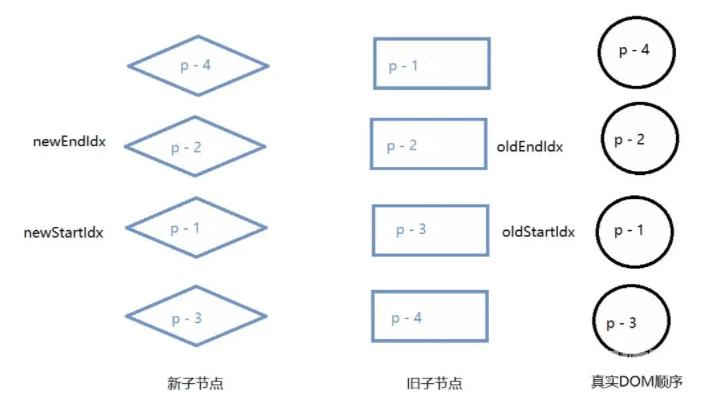
最后while条件为假,退出diff
code
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
patch(oldStartVNode, newStartVNode, container)
oldStartVNode = oldChildren[++oldStartIdx]
newStartVNode = newChildren[++newStartIdx]
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
// 调用patch打补丁
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
patch(oldStartVNode, newEndVNode, container)
insert(oldStartVNode.el, container, newEndVNode.el.nextSibling)
oldStartVNode = oldChildren[++oldStartIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
// 调用patch打补丁
patch(oldEndVNode, newStartVNode, container)
// 移动DOM操作 oldEndVNode.el移动 到 oldStartVNode.el 前面
insert(oldEndVNode.el, container, oldStartVNode.el)
// 移动DOM操作完成后
oldEndVNode = oldChildren[--oldEndVNode]
newStartVNode = newChildren[++newStartVNode]
}
}
双端Diff的优势
回到最开始的例子,使用双端Diff比较的时候,第一次循环的步骤四就能找到对应 p - 3的节点,然后将其移动到p - 1之前。
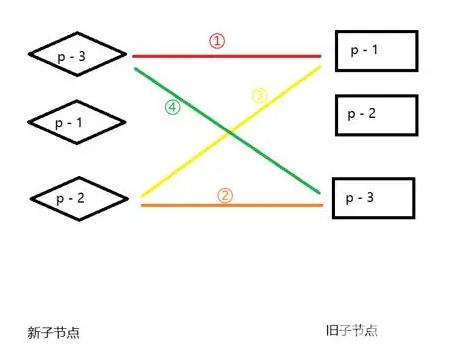
只需要一次DOM操作就能完成更新。
非理想情况的处理方式
上面是一个比较理想的例子,四个步骤分别都能匹配到对应的元素,实际上并非所有情况都能匹配到。
比如 - 案例三
newChildren: [
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '4', key: '4' },
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '3', key: '3' }
],
oldChildren: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' },
{ type: 'p', children: '4', key: '4' }
]
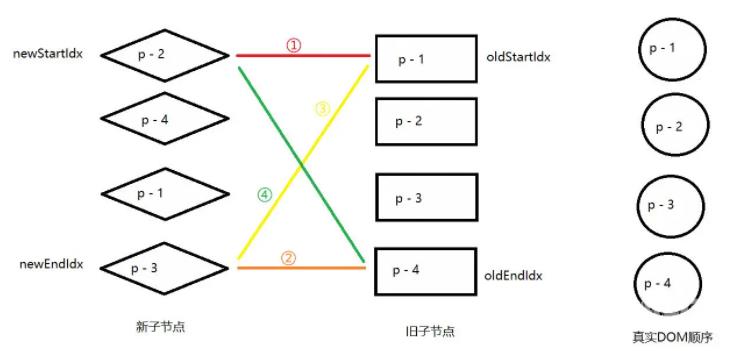
进行第一轮比较时,无法命中四个步骤中的任何一步。
- p - 1 === p - 2
- p - 4 === p - 3
- p - 1 === p - 3
- p - 4 === p - 2
因此只能通过额外的步骤来处理非理想情况。头部尾部都不能命中,那么旧看非头/尾部的节点能否命中,拿新的一组子节点的头部节点去旧的一组子节点中查找。
在旧的一组子节点中,找到与新的一组子节点头部节点具有相同key值的节点,意味着要将找到的子节点移动到真实DOM的头部。
查找结果如图
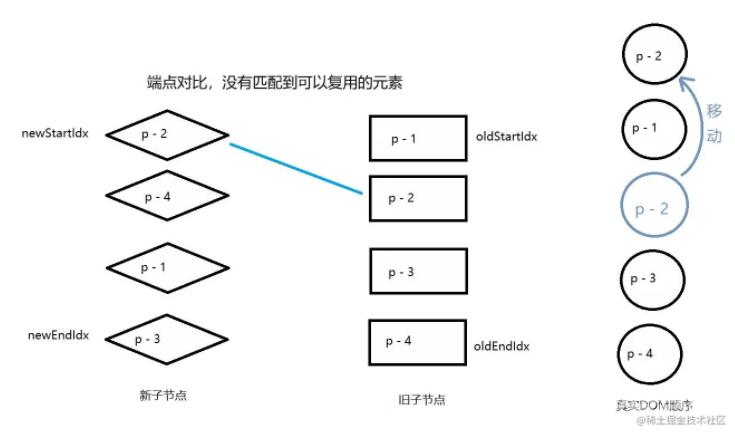
code
对应功能代码
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
} else {
// 上面四个步骤都没有命中
// 遍历旧的一组子节点,视图寻找与newStartVNode拥有相同key值的节点
// idInOld就是新的一组子节点的头部节点在旧的一组子节点中的索引
const idInOld = oldChildren.findIndex(
node => node.key === newStartVNode.key
)
// idInOld > 0说明找到了可复用的节点,并且需要将其对应的真实DOM移动到头部
if (idInOld > 0) {
// 找到匹配到的节点,也就是需要移动的节点
const vNodeToMove = oldChildren[idInOld]
// 调用 patch 更新
patch(vNodeToMove, newStartVNode, container)
// 将vNodeToMove插入到头部节点oldStartVNode.el之前
insert(vNodeToMove.el, container, oldStartVNode.el)
// 由于位置 idInOld 处的节点对应的真实DOM已经发生移动,因此将其设置为 undefined
oldChildren[idInOld] = undefined
// 最后更新 newStartVNode 到下一个位置
newStartVNode = newChildren[++newStartVNode]
}
}
}
接下来第二个和第三个新节点都可以通过双端对比找到匹配的节点,过程与 第二个案例 同理。
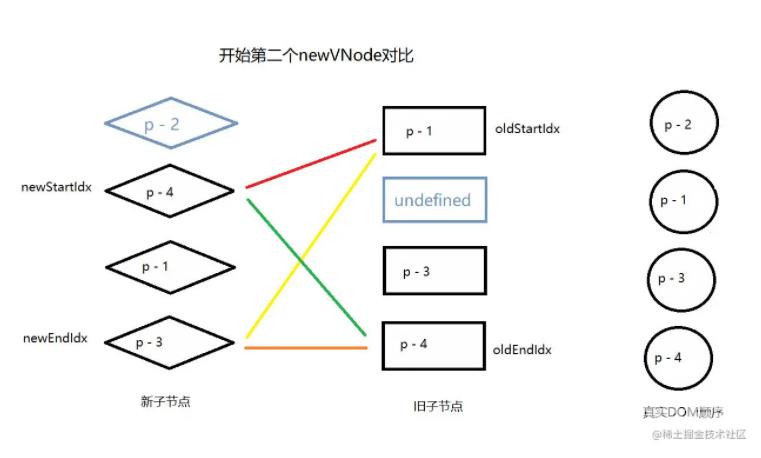
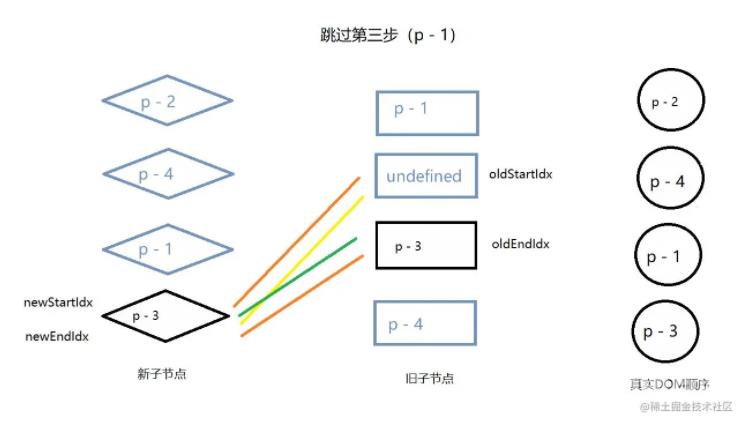
直到最后一个节点,此时旧节点列表的头部节点是 undefined,因为该节点已经被处理过了,所以不需要再处理它,直接跳过即可。
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
// 如果头部或尾部节点为undefined,说明已经处理过了,直接跳过
if (!oldStartVNode) {
oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
oldEndVNode = oldChildren[--oldEndIdx]
} else if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
} else {
}
}
}
接下来的情况与上个案例同理。
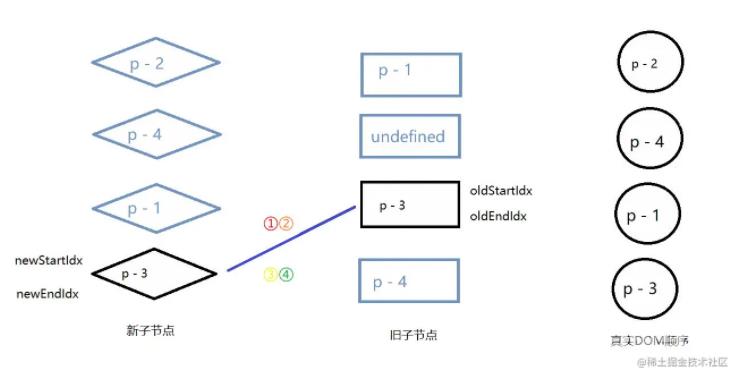
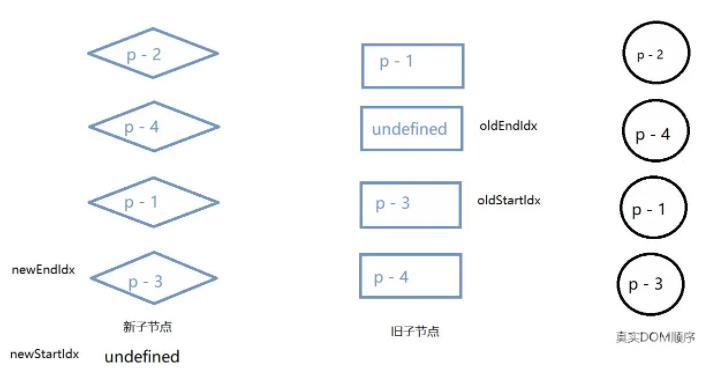
添加新元素
当我们拿新的一组子节点中的头部节点去旧的一组子节点中寻找可复用节点时,并不是一定能找到。
案例四
newChildren: [
{ type: 'p', children: '4', key: '4' },
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '3', key: '3' },
{ type: 'p', children: '2', key: '2' }
],
oldChildren: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' }
]
双端查找没有匹配到
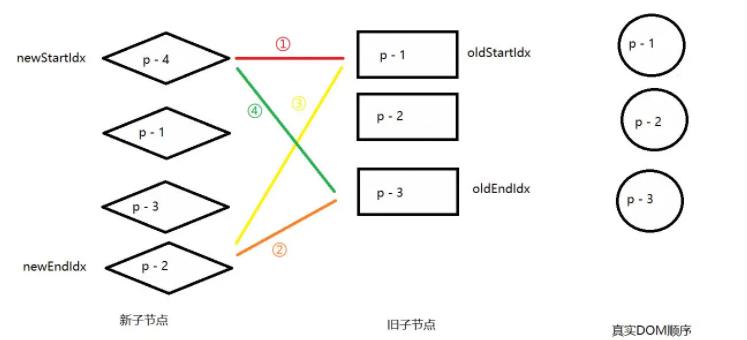
循环查找也没有匹配到
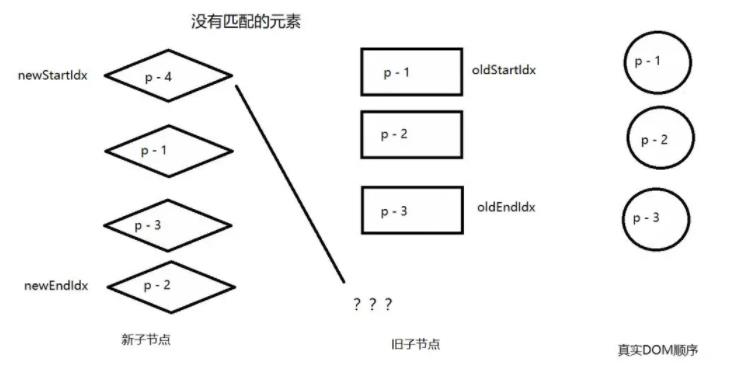
p - 4经过双端对比,循环查找都没有找到匹配的节点,说明 p - 4 是一个新增节点,应该将它创建并挂载到正确的位置。
那么应该挂载到什么位置呢,因为节点p - 4时新的一组子节点中的头部节点,所以只需要将它挂载到当前头部节点之前即可。头部节点指的是旧的一组子节点中的头部节点对应的真实DOM节点 p - 1。
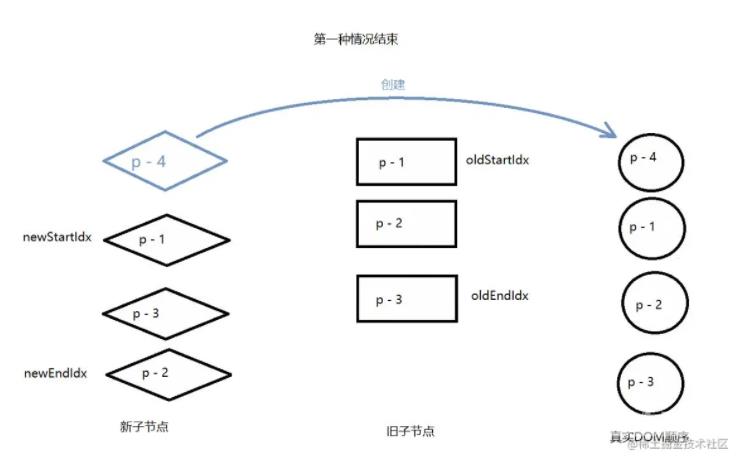
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
} else {
// 上面四个步骤都没有命中
// 遍历旧的一组子节点,视图寻找与newStartVNode拥有相同key值的节点
// idInOld就是新的一组子节点的头部节点在旧的一组子节点中的索引
const idInOld = oldChildren.findIndex(
node => node.key === newStartVNode.key
)
// idInOld > 0说明找到了可复用的节点,并且需要将其对应的真实DOM移动到头部
if (idInOld > 0) {
// 找到匹配到的节点,也就是需要移动的节点
const vNodeToMove = oldChildren[idInOld]
// 调用 patch 更新
patch(vNodeToMove, newStartVNode, container)
// 将vNodeToMove插入到头部节点oldStartVNode.el之前
insert(vNodeToMove.el, container, oldStartVNode.el)
// 由于位置 idInOld 处的节点对应的真实DOM已经发生移动,因此将其设置为 undefined
oldChildren[idInOld] = undefined
// 最后更新 newStartVNode 到下一个位置
newStartVNode = newChildren[++newStartVNode]
} else {
// 将 newStartVNode作为新节点挂载到头部,使用当前头部节点 oldStartVNode.el 作为锚点
patch(null, newStartVNode, container, oldStartVNode.el)
}
// 更新头部节点
newStartVNode = newChildren[++newStartIdx]
}
}
当条件 idInOld > 0不成立时,说明没有可以复用的节点,又由于newStartVNode是头部节点,因此应该将其作为新的头部节点进行挂载操作。
剩下节点的操作类似于案例二。
新增节点可能在最后一次匹配到 - 案例五
newChildren: [
{ type: 'p', children: '4', key: '4' },
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' }
],
oldChildren: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' }
]
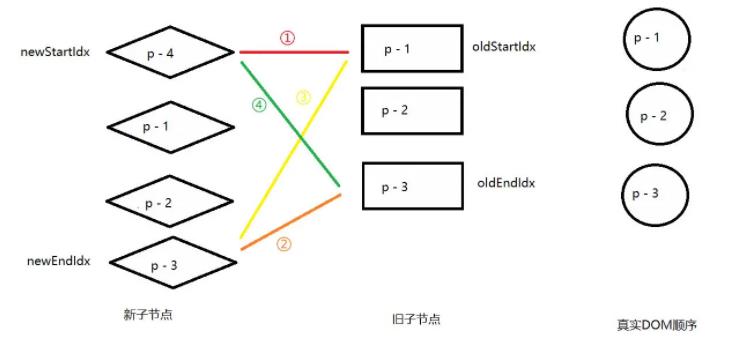

这里省去双端匹配的流程
由于变量oldStartIdx 的值大于oldEndIdx的值,满足更新停止的条件,更新停止了。但看图可知,p - 4在整个更新过程中被一楼了,没有得到任何处理。
因此可得:新的一组子节点中有一六得节点需要作为新节点挂载。索引值位于newStartIdx 和 newEndIdx 之间得所有节点都是新节点。挂载时得锚点仍然使用当前头部节点 oldStartVNode.el。
因为此时旧节点列表中得节点可能为undefined,因此可能出现问题;但新节点列表得顺序已经被更新了,所以更新过得新节点对应得真实DOM顺序都已经重新牌列,便可以取锚点:
const anchor = newChildren[newEndIdx + 1] ? newChildren[newEndIdx + 1].el : null
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
}
// 说明有新节点需要挂载
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
for (let i = newStartIdx; i < newEndIdx; i++) {
const anchor = newChildren[newEndIdx + 1] ? newChildren[newEndIdx + 1].el : null
patch(null, newChildren[i], container, anchor)
}
}
移除不存在得节点
除了新增节点得问题后,还可能存在需要移除的节点 - 案例六
newChildren: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '3', key: '3' }
],
oldChildren: [
{ type: 'p', children: '1', key: '1' },
{ type: 'p', children: '2', key: '2' },
{ type: 'p', children: '3', key: '3' }
]
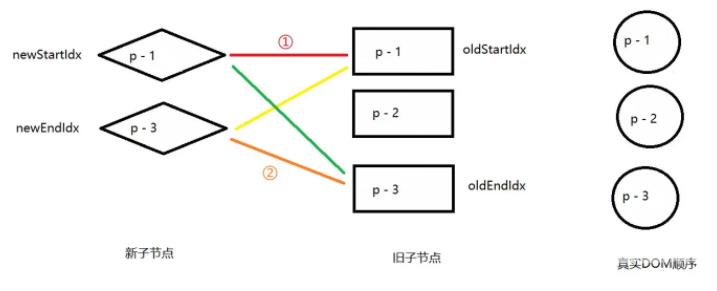
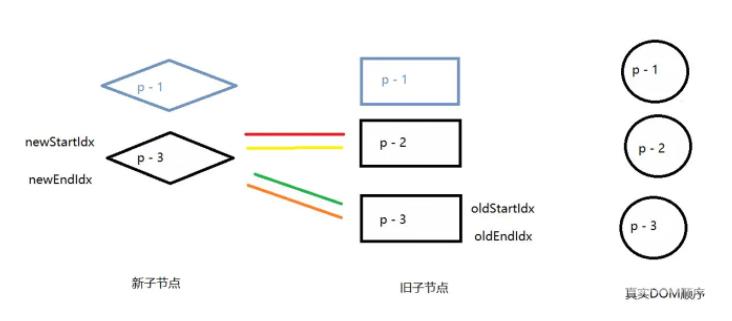
第一次、第二次循环的步骤于案例二同理
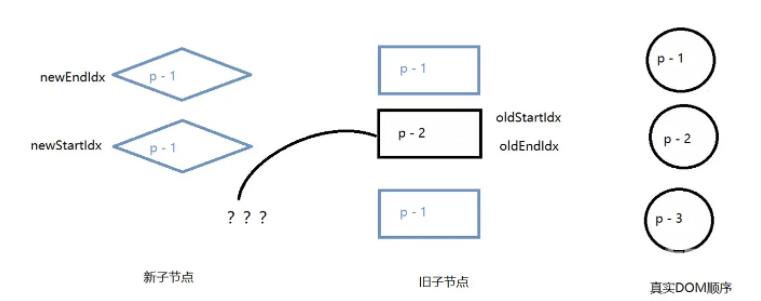
新节点更新完之后,发现还存在未处理的旧节点,这便是需要删除的节点。
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
}
// 说明有新节点需要挂载
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
for (let i = newStartIdx; i < newEndIdx; i++) {
const anchor = newChildren[newEndIdx + 1] ? newChildren[newEndIdx + 1].el : null
patch(null, newChildren[i], container, anchor)
}
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
// 有需要删除的节点
for (let i = oldStartIdx; i < oldEndIdx; i++) {
unmount(oldChildren[i])
}
}
双端Diff完整代码
function patchKeyedChildren (n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
// 四个端点指针
let newStartIdx = 0
let newEndIdx = newChildren.length - 1
let oldStartIdx = 0
let oldEndIdx = oldChildren.length - 1
// 四个端点元素
let newStartVNode = newChildren[newStartIdx]
let newEndVNode = newChildren[newEndIdx]
let oldStartVNode = oldChildren[oldStartIdx]
let oldEndVNode = oldChildren[oldEndIdx]
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 开始Diff
// 如果头部或尾部节点为undefined,说明已经处理过了,直接跳过
if (!oldStartVNode) {
oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
oldEndVNode = oldChildren[--oldEndIdx]
} else if (oldStartVNode.key === newStartVNode.key) {
// 第一步 oldStartVNode - newStartVNode
patch(oldStartVNode, newStartVNode, container)
oldStartVNode = oldChildren[++oldStartIdx]
newStartVNode = newChildren[++newStartIdx]
} else if (oldEndVNode.key === newEndVNode.key) {
// 第二步 oldEndVNode - newEndVNode
// 调用patch打补丁
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
// 第三步 oldStartVNode - newEndVNode
patch(oldStartVNode, newEndVNode, container)
insert(oldStartVNode.el, container, newEndVNode.el.nextSibling)
oldStartVNode = oldChildren[++oldStartIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
// 第四步 oldEndVNode - newStartVNode
// 调用patch打补丁
patch(oldEndVNode, newStartVNode, container)
// 移动DOM操作 oldEndVNode.el移动 到 oldStartVNode.el 前面
insert(oldEndVNode.el, container, oldStartVNode.el)
// 移动DOM操作完成后
oldEndVNode = oldChildren[--oldEndVNode]
newStartVNode = newChildren[++newStartVNode]
} else {
// 上面四个步骤都没有命中
// 遍历旧的一组子节点,视图寻找与newStartVNode拥有相同key值的节点
// idInOld就是新的一组子节点的头部节点在旧的一组子节点中的索引
const idInOld = oldChildren.findIndex(
node => node.key === newStartVNode.key
)
// idInOld > 0说明找到了可复用的节点,并且需要将其对应的真实DOM移动到头部
if (idInOld > 0) {
// 找到匹配到的节点,也就是需要移动的节点
const vNodeToMove = oldChildren[idInOld]
// 调用 patch 更新
patch(vNodeToMove, newStartVNode, container)
// 将vNodeToMove插入到头部节点oldStartVNode.el之前
insert(vNodeToMove.el, container, oldStartVNode.el)
// 由于位置 idInOld 处的节点对应的真实DOM已经发生移动,因此将其设置为 undefined
oldChildren[idInOld] = undefined
// 最后更新 newStartVNode 到下一个位置
newStartVNode = newChildren[++newStartVNode]
} else {
// 将 newStartVNode作为新节点挂载到头部,使用当前头部节点 oldStartVNode.el 作为锚点
patch(null, newStartVNode, container, oldStartVNode.el)
}
// 更新头部节点
newStartVNode = newChildren[++newStartIdx]
}
}
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
// 说明有新节点需要挂载
for (let i = newStartIdx; i < newEndIdx; i++) {
const anchor = newChildren[newEndIdx + 1] ? newChildren[newEndIdx + 1].el : null
patch(null, newChildren[i], container, anchor)
}
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
// 有需要删除的节点
for (let i = oldStartIdx; i < oldEndIdx; i++) {
unmount(oldChildren[i])
}
}
}
以上就是Vue3 diff算法之双端diff算法详解的详细内容,更多关于Vue3双端diff算法的资料请关注易盾网络其它相关文章!
