文章目录
- KNN算法原理
- KNN算法介绍
- KNN算法模型
- 距离度量
- k值的选择
- 分类的决策规则
- KNN算法python实现
- 手写数字识别
- sklearn代码实现
- 参考文献
KNN算法原理
KNN算法介绍
KNN（K-Nearest Neighbor）算法，顾名思义，其原理也就是“近朱者赤，近墨者黑”。KNN算法是一种有监督的分类算法，输入同样为样本特征值向量以及对应的类标签，输出则为具有分类功能的模型，能够根据输入的特征值预测分类结果。核心原理就是，与待分类点最近的K个邻居中，属于哪个类别的多，待分类点就属于那个类别。
KNN分类算法的思路很简洁，实现也很简洁，具体分三步： 1）找K个最近邻。KNN分类算法的核心就是找最近的K个点，选定度量距离的方法之后，以待分类样本点为中心，分别测量它到其他点的距离，找出其中的距离最近的“TOP K”，这就是K个最近邻。 2）统计最近邻的类别占比。确定了最近邻之后，统计出每种类别在最近邻中的占比。 3）选取占比最多的类别作为待分类样本的类别。
KNN算法模型
KNN算法模型主要有三要素构成：距离度量，k值的选择和分类的决策规则。
距离度量
两个样本点之间的距离代表了这两个样本之间的相似度。距离越大，差异性越大；距离越小，相似度越大。 闵可夫斯基距离的数学表达式如下：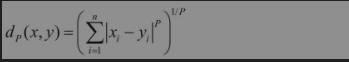
闵可夫斯基距离是一组距离的定义，不妨把闵可夫斯基距离看作一个代数形式的母版，通过给P设置不同的值，就能用闵可夫斯基距离得到不同的距离表达式。
当P=1时，称为曼哈顿距离，表达式如下：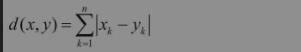
当P=2时，为欧几里得距离，最常用于度量两点之间的直线距离。表达式如下：
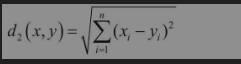距离的度量方法没有好坏，选择什么方法主要是根据当前情况而定。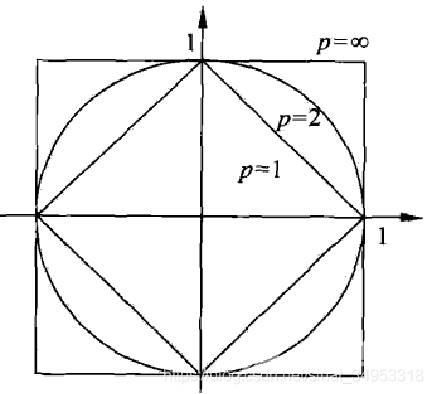
k值的选择
k值的选择会对KNN算法的结果产生重大的影响。
如果选择较小的K值 “学 习”的近似误差（approximation error)会减小，但 “学习”的估计误差（estimation error) 会增大， 噪声敏感 K值的减小就意味着整体模型变得复杂，容易发生过 拟合.
如果选择较大的K值 减少学习的估计误差，但缺点是学习的近似误差会增大. K值的增大 就意味着整体的模型变得简单.
在应用中，k值一般取一个比较小的数值，通常采用交叉验证法来选取最优的k值。
分类的决策规则
根据多数表决原则，决定待分类样本点的类别。
KNN算法python实现
手写数字识别
1）数据加载：我们可以直接从 sklearn 中加载自带的手写数字数据集； 2）准备阶段：通过可视化的方式来查看图像的呈现。通过数据规范化可以让数据都在同一个数量级的维度。将全部的图像数据作为特征值矩阵； 3）分类阶段：通过训练可以得到分类器，然后用测试集进行准确率的计算。
knn分类器的常用构造参数有： 1）.n_neighbors 代表邻居的数量。 2）.weights： 代表所有邻居的权重，其中 uniform 代表所有邻居权重相同， distance 代表权重是距离的倒数。还可以自定义。 3）.algorithm: 计算邻居的方法，auto代表 根据数据的情况自动选择，kd_tree 是kd树，适用于维数不超过20的情况。ball_tree是球树，可以用于维度更大的情况。brute 是暴力搜索。 4）.leaf_size:是kd树或者球树的叶子数量，默认是20.
sklearn代码实现
from sklearn.model_selection import train_test_splitfrom sklearn import preprocessingfrom sklearn.metrics import accuracy_scorefrom sklearn.datasets import load_digitsfrom sklearn.neighbors import KNeighborsClassifierimport matplotlib.pyplot as plt
#加载数据digits = load_digits()data = digits.data#数据探索print(data.shape)
(1797, 64)
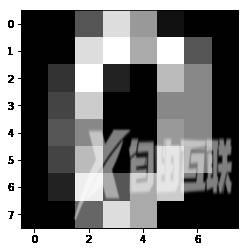
# 查看第一幅图像print(digits.images[0])
[[ 0. 0. 5. 13. 9. 1. 0. 0.] [ 0. 0. 13. 15. 10. 15. 5. 0.] [ 0. 3. 15. 2. 0. 11. 8. 0.] [ 0. 4. 12. 0. 0. 8. 8. 0.] [ 0. 5. 8. 0. 0. 9. 8. 0.] [ 0. 4. 11. 0. 1. 12. 7. 0.] [ 0. 2. 14. 5. 10. 12. 0. 0.] [ 0. 0. 6. 13. 10. 0. 0. 0.]]
# 第一幅图像代表的数字含义print(digits.target[0])
0
# 将第一幅图像显示出来plt.gray()plt.imshow(digits.images[0])plt.show()
# 分割数据，将25%的数据作为测试集，其余作为训练集train_x, test_x, train_y, test_y = train_test_split(data, digits.target, test_size=0.25, random_state=33)
# 采用Z-Score规范化ss = preprocessing.StandardScaler()train_ss_x = ss.fit_transform(train_x)test_ss_x = ss.transform(test_x)
# 创建KNN分类器knn = KNeighborsClassifier(n_neighbors=4)knn.fit(train_ss_x, train_y) predict_y = knn.predict(test_ss_x) print("KNN准确率: %.4lf" % accuracy_score(test_y, predict_y))
KNN准确率: 0.9733
代码中，我使用了 train_test_split 做数据集的拆分，使用 matplotlib.pyplot 工具包显示图像，使用 accuracy_score 进行分类器准确率的计算，使用 preprocessing 中的 StandardScaler 和 MinMaxScaler 做数据的规范化。
参考文献
李航.统计学习方法（第2版） 陈旸.数据分析实战45讲
版权声明：本文为sinat_34953318原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。原文链接：https://blog.csdn.net/sinat_34953318/article/details/107309329