【论文阅读】SemiSupervisedLearningwithLadderNetworks

论文地址: Semi-Supervised Learning with Ladder Networks 会议: NIPS 2015 任务: 半监督分类

我们将监督学习与深度神经网络中的无监督学习相结合。所提出的模型经过训练可以通过反向传播同时最小化监督和非监督成本函数的总和从而避免了分层预训练的需要。我们的工作建立在 Valpola 提出的梯形网络之上我们通过将模型与监督相结合来扩展该梯形网络。

本文主要是在前任的深度半监督模型上添加了一些适配以完成半监督任务。阅读这篇论文需要一些前置知识貌似是有两个版本一个是会议的NIPS,内容精炼不太容易读懂还有一个版本是arxiv的较为详细。

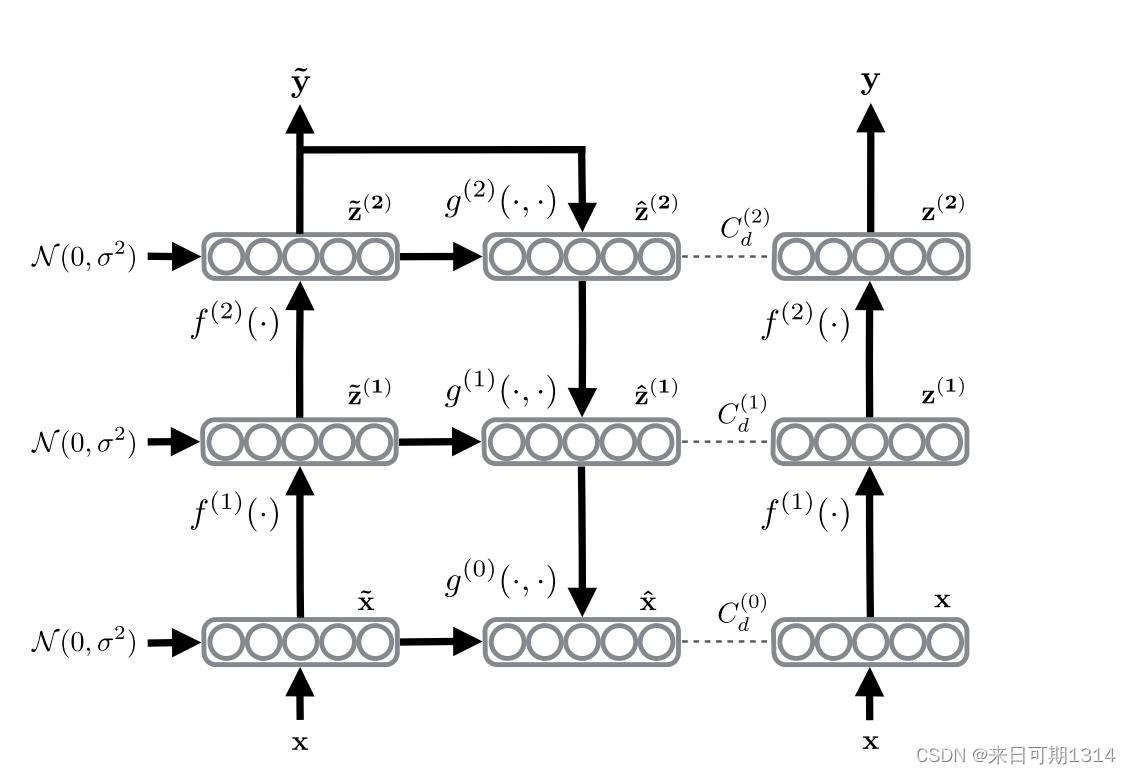
结合这两张图大致的计算流程算是比较清晰了。

这里主要是讨论一下算法中对于损失的计算。

输入数据 有标签数据 {x(n),t(n)∣1≤n≤N}\{\mathbf{x}(n), t(n) \mid 1 \leq n \leq N\} {x(n),t(n)∣1≤n≤N} 其中对于任意样本x(i)\mathbf{x}(i)x(i)的标签为t(i)t(i)t(i)1≤i≤N1 \leq i \leq N1≤i≤N。 无标签数据 {x(n)∣1≤n≤N}\{\mathbf{x}(n) \mid 1 \leq n \leq N\} {x(n)∣1≤n≤N}

CCcCd(1)CC_{\mathrm{c}}C_{\mathrm{d}}\tag{1} CCc​Cd​(1) 首先损失分为两个部分一个是有监督的损失CcC_{\mathrm{c}}Cc​另外一个是无监督的损失CdC_{\mathrm{d}}Cd​。

Cc−1N∑n1Nlog⁡P(y~t(n)∣x(n))(2)C_{\mathrm{c}}-\frac{1}{N} \sum_{n1}^{N} \log P(\tilde{\mathbf{y}}t(n) \mid \mathbf{x}(n))\tag{2} Cc​−N1​n1∑N​logP(y~​t(n)∣x(n))(2) 这个是有监督损失是分类常用的交叉熵损失。其中y~\tilde{\mathbf{y}}y~​表示的感觉有点问题是说对一个样本的预测值没什么没有下标。 Cd∑l0LλlCd(l)∑l0LλlNml∑n1N∥z(l)(n)−z^BN(l)(n)∥2(3)C_{\mathrm{d}}\sum_{l0}^{L} \lambda_{l} C_{\mathrm{d}}^{(l)}\sum_{l0}^{L} \frac{\lambda_{l}}{N m_{l}} \sum_{n1}^{N}\left\|\mathbf{z}^{(l)}(n)-\hat{\mathbf{z}}_{\mathrm{BN}}^{(l)}(n)\right\|^{2}\tag{3} Cd​l0∑L​λl​Cd(l)​l0∑L​Nml​λl​​n1∑N​∥∥∥​z(l)(n)−z^BN(l)​(n)∥∥∥​2(3) 这个是无监督损失损失定义了不同层经过去噪与干净数据前向值的差异的加权和其中权值定义了每个层损失的重要程度不同。

Notice 在论文实验中处理的数据集是MNIST但是在论文中表述的确是"permutation invariant MNIST"。经过多方检索确认应该是对于手写数字图片的像素点不知道二维位置信息也就是说无法经过卷积提取特征可以理解为图片像素被强行展开成一维向量所以在原文中会说该任务相较于原任务更难。