二叉链表和职工管理系统结合_数据结构之二叉树概念

首先我们来讲讲什么是树树是一种非线性的数据结构相对于线性的数据结构(链表、数组)而言树的平均运行时间更短(往往与树相

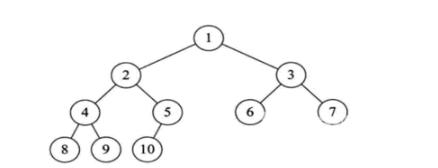
首先我们来讲讲什么是树

• 树是一种非线性的数据结构相对于线性的数据结构(链表、数组)而言树的平均运行时间更短(往往与树相关的排序时间复杂度都不会高)

在现实生活中我们一般的树长这个样子的

但是在编程的世界中我们一般把树“倒”过来看这样容易我们分析

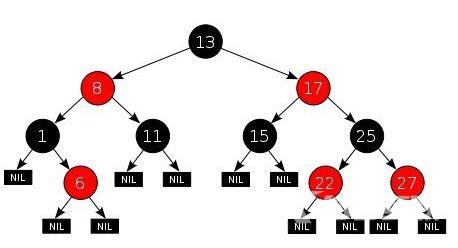
一般的树是有很多很多个分支的分支下又有很多很多个分支如果在程序中研究这个会非常麻烦。因为本来树就是非线性的而我们计算机的内存是线性存储的太过复杂的话我们无法设计出来的。

如图

不能确定每个节点下有多少分支所以设计的时候就非常的不方便

因此我们先来研究简单又经常用的—> 二叉树

二叉树是树的特殊一种具有如下特点

1、每个结点最多有两颗子树结点的度最大为2。

2、左子树和右子树是有顺序的次序不能颠倒。

3、即使某结点只有一个子树也要区分左右子树。

一、特殊的二叉树及特点

1、斜树

所有的结点都只有左子树(左斜树)或者只有右子树(右斜树)。这就是斜树应用较少

2、满二叉树

所有的分支结点都存在左子树和右子树并且所有的叶子结点都在同一层上这样就是满二叉树。就是完美圆满的意思关键在于树的平衡。

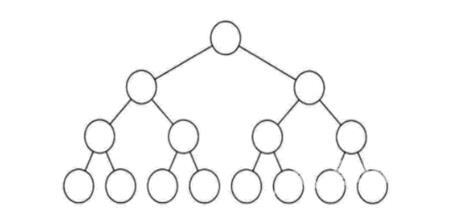
根据满二叉树的定义得到其特点为

叶子只能出现在最下一层。

非叶子结点度一定是2.

在同样深度的二叉树中满二叉树的结点个数最多叶子树最多。

3、完全二叉树

对一棵具有n个结点的二叉树按层序排号如果编号为i的结点与同样深度的满二叉树编号为i结点在二叉树中位置完全相同就是完全二叉树。满二叉树必须是完全二叉树反过来不一定成立。

其中关键点是按层序编号然后对应查找。

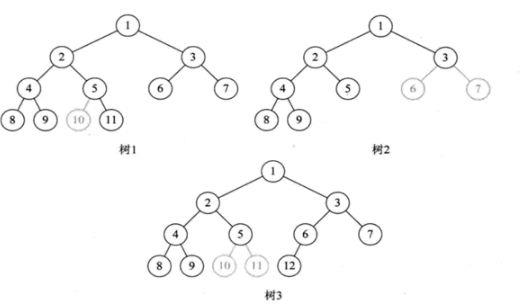
在上图中树1按层次编号5结点没有左子树有右子树10结点缺失。树2由于3结点没有字数是的6,7位置空挡了。树3中结点5没有子树。

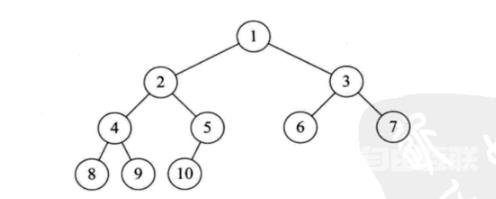
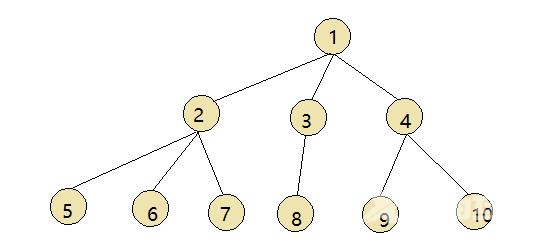
上图就是一个完全二叉树。

结合完全二叉树定义得到其特点

叶子结点只能出现在最下一层(满二叉树继承而来)

最下层叶子结点一定集中在左 部连续位置。

倒数第二层如有叶子节点一定出现在右部连续位置。

同样结点树的二叉树完全二叉树的深度最小(满二叉树也是对

的)。

根据下图加深理解什么时候是完全二叉树。

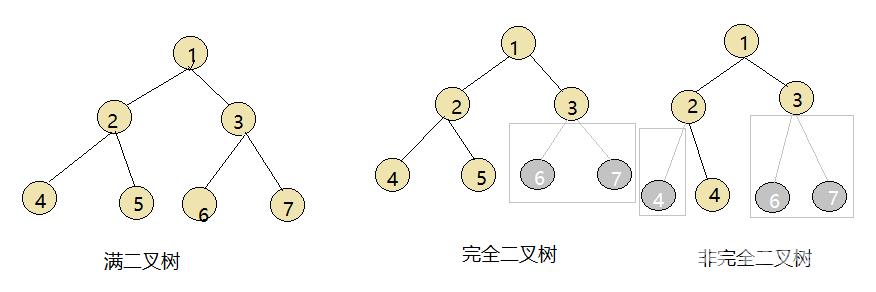
第二个图去掉灰色框框内的节点其他节点编号(连续)与满二叉树一样

第三个图去掉灰色框框内的节点前图编号为5的变成了4编号不一样所以不是完全二叉树

这是最简单的判断方法

三、二叉树性质

1、一般二叉树性质

1、在非空二叉树的i层上至多有2^i-1个节点(i>1)。通过归纳法论证。

2、在深度为K的二叉树上最多有2^k-1个结点(k>1)。通过归纳法论证。

3、对于任何一棵非空的二叉树,如果叶节点个数为n₀度数为2的节点个数为n₂则有: n0 n₂  1

在一棵二叉树中除了叶子结点(度为0)之外就剩下度为2(n2)和1(n1)的结点了。则树的结点总数为T n0n1n2;在二叉树中结点总数为T而连线数为T-1.所以有n0n1n2-1 2*n2 n1;最后得到n0 n21;

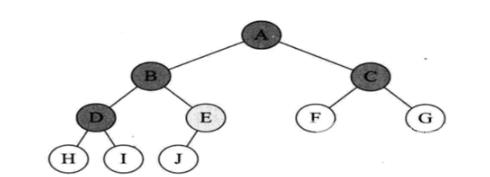
上图中结点总数是10n2为4n1为1n0为5

2、完全二叉树性质

a、具有n的结点的完全二叉树的深度为log₂n1.

满二叉树是完全二叉树对于深度为k的满二叉树中结点数量是2^k-1 n完全二叉树结点数量肯定最多2^k-1,同时完全二叉树倒数第二层肯定是满的(倒数第一层有结点那么倒是第二层序号和满二叉树相同)所以完全二叉树的结点数最少大于少一层的满二叉树为2^k-1-1。

根据上面推断得出 2^k-1-1k-1因为结点数Nn为整数那么n<2^k-1可以推出n<2^k ,n>2^k-1-1可以推出 n>2^k-1,所以2^k-1k  。即可得k-12n2n]1。

b、如果有一颗有n个节点的完全二叉树的节点按层次序编号对任一层的节点i(1

    1.如果i1则节点是二叉树的根无双亲如果i>1则其双亲节点为[i/2]向下取整

    2.如果2i>n那么节点i没有左孩子否则其左孩子为2i

    3.如果2i1>n那么节点没有右孩子否则右孩子为2i1

在上图中验证

第一条

当i1时为根节点。当i>1时比如结点为7他的双亲就是7/2 3结点9双亲为4.

第二条

结点6,6*2 12>10所以结点6无左孩子是叶子结点。结点55*2 10左孩子是10,结点4为8.

第三条

结点52*51>10,没有右孩子结点4则有右孩子。

好了本篇文章就讲到这里大家花时间好好消化消化下篇文章直接上代码带大家进一步深入了解二叉树

【转自：东台网页开发公司 http://www.1234xp.com/dongtai.html 提供，感恩】