1、问题描述
公鸡5文钱一只母鸡3文钱一只小鸡3只一文钱用100文钱买一百只鸡其中公鸡母鸡小鸡都必须要有问公鸡母鸡小鸡要买多少只刚好凑足100文钱。
2、算法分析
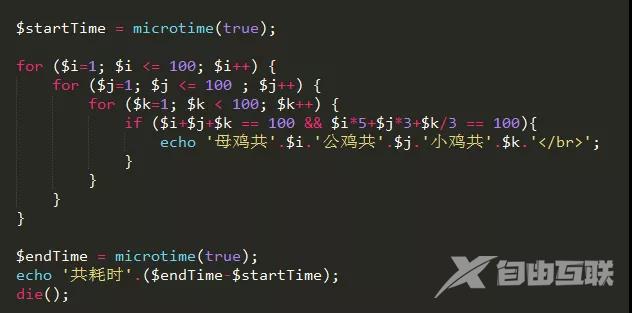
这是这个问题最常规的解法看下程序的运行结果。
母鸡共4公鸡共18小鸡共78 母鸡共8公鸡共11小鸡共81 母鸡共12公鸡共4小鸡共84 共耗时0.36380910873413
这个算法是可以得到问题的答案但是算法的时间复杂度为O(N3)我们可以尝试优化该算法使其时间复杂度降到O(N)。
3、算法优化
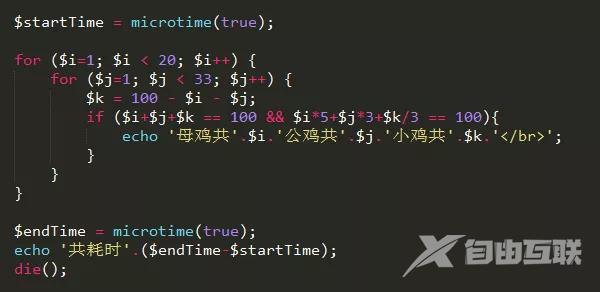
首先根据问题分析了母鸡、公鸡的取值范围再通过代数式运算得到小鸡的取值范围这样通过人为分析缩小参数范围直接就减少了很多不必要的运算从而提高了算法效率。
母鸡共4公鸡共18小鸡共78 母鸡共8公鸡共11小鸡共81 母鸡共12公鸡共4小鸡共84 共耗时0.00051999092102051
运行速度提高了将近1000倍。
再来看第二个优化。
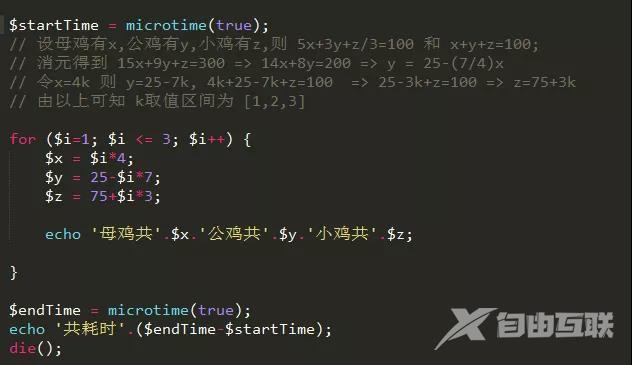
设母鸡有x公鸡有y小鸡有z则 5x3yz/3100 和 xyz100
消元得到 15x9yz300 > 14x8y200 > y 25-(7/4)x
令x4k 则 y25-7k 4k25-7kz100 > 25-3kz100 > z753k
由以上可知 k取值区间为 [1,2,3]
这个优化也是首先通过数学方程消元来得到各个变量的一元一次方程再结合已知条件确定参数的范围这个优化后的算法时间复杂度降为O(N)。
程序运行结果为
母鸡共4公鸡共18小鸡共78 母鸡共8公鸡共11小鸡共81 母鸡共12公鸡共4小鸡共84 共耗时1.978874206543E-5
其中1.978874206543E-5 0.0000197887
相对上一步优化速度提升了20多倍。
感受到数学的魅力了吧所以说数学才是算法的基础呢。
