普通二叉搜索树剖析

二叉搜索树概述

二叉搜索树是一种具有特殊性质的二叉树。二叉搜索树可以是一棵空树，若不为空树，其：

• 若左子树不为空，则左子树所有的节点值小于根节点值；
• 若右子树不为空，则右子树所有的节点值大于根节点值。

与二叉树一样，二叉搜索树也是递归定义的，二叉搜索树的左右子树都是二叉搜索树。

二叉搜索树的结构

二叉搜索树的结构是一棵二叉树，其左子树的节点值都小于根节点值，右子树的节点值都大于根节点值。二叉搜索树使用链式结构进行实现。

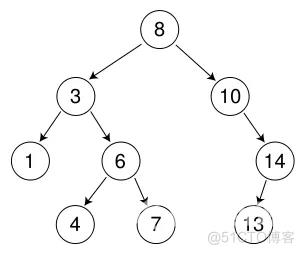
两种二叉搜索树及定义

二叉搜索树常用有两种模型：Key模型和Key-Value模型。

Key模型的二叉搜索树的节点只需要存储一个关键码Key即可，可以将关键码理解为需要搜索的值。这种模型主要用于解决快速判断一个值在不在集合中的问题。

template<typename Key>
struct BinarySearchTreeNode
{
    typedef BinarySearchTreeNode<Key> BST_Node;

    BinarySearchTreeNode(const Key& val)
        :_left(nullptr),
    	_right(nullptr),
    	_val(val)
    { };

    BST_Node* _left;
    BST_Node* _right;
    Key _val; //只存储一个关键码
};

template<typename Key>
class BinarySearchTree	
{
private:		
    typedef BinarySearchTreeNode<Key> BST_Node;
    typedef BinarySearchTree<Key> Self;
    
    /*…………*/
 
private:
    BST_Node* _root; //维护根节点
};

Key-Value模型的二叉搜索树的节点除了要存储关键码Key之外，还需要存储对应的键值Value，即需要存储一个(Key, Value)的键值对。这种模型主要用于解决通过一个值找另外一个值的映射问题。

template<typename Key, typename Value>
struct BinarySearchTreeNode
{
    typedef BinarySearchTreeNode<Key, Value> BST_Node;

    BinarySearchTreeNode<Key, Value>(const Key& k, const Value& v)
      :_key(k), _val(v),
    _left(nullptr), _right(nullptr)
    { }

    Key _key;
    Value _val; //存储一个键值对
    BST_Node* _left;
    BST_Node* _right;
};

template<typename Key, typename Value>
class BinarySearchTree
{
private:
  typedef BinarySearchTreeNode<Key, Value> BST_Node;
  
  /*…………*/
 
private:
  	BST_Node* _root;
};

上述的两种模型，前者是STL set的基本实现思路，后者是STL map的基本实现思路，二者的Key值都具有互异性，不允许重复。

二叉搜索树的接口实现

作为一种具有特殊性质的二叉树，二叉搜索树的接口大体上有两种实现方式：迭代方式实现和递归方式实现。下面的实现以Key-Value模型为例，Key模型与此类似。

迭代方式实现

template<typename Key, typename Value>
struct BinarySearchTreeNode
{
  typedef BinarySearchTreeNode<Key, Value> BST_Node;
  
  BinarySearchTreeNode<Key, Value>(const Key& k, const Value& v)
    :_key(k), _val(v),
 		 _left(nullptr), _right(nullptr)
  { }

  Key _key;
  Value _val;
  //存储一个键值对
  BST_Node* _left;
  BST_Node* _right;
};

template<typename Key, typename Value>
class BinarySearchTree
{
  private:
  typedef BinarySearchTreeNode<Key, Value> BST_Node;
  typedef BinarySearchTree<Key, Value> Self;

public:
  BinarySearchTree()
    :_root(nullptr)
    { }

  BinarySearchTree(const Self& BSTree)
  {
    //递归进行拷贝构造
    _root = _copyConstruct(BSTree);
  }

  ~BinarySearchTree()
  {
    Destroy(_root); //递归销毁二叉树
  }
  //现代写法的赋值重载
  Self& operator=(Self BSTree) const
  {
    std::swap(_root, BSTree._root);
    return *this;
  }

  bool Insert(const Key& key, const Value& val)
  {
    //树为空的情况单独处理
    if (Empty()) {
      _root = new BST_Node(key, val);
    }
    BST_Node* cur = _root;
    BST_Node* parent = nullptr;
    //寻找合适的插入位置
    while (cur)
    {
      if (key < cur->_key) {
        parent = cur;
        cur = cur->_left;
      }
      else if (key > cur->_key) {
        parent = cur;
        cur = cur->_right;
      }
      else {
        return false;
      }
    }
    BST_Node* newNode = new BST_Node(key, val);
    //插入新节点
    //由于不能判断此时cur相对于parent的位置，所以需要再次判断
    if (key < parent->_key) {
      parent->_left = newNode;
    }
    else {
      parent->_right = newNode;
    }
    return true;
  }

  bool Erase(const Key& key)
  {
    BST_Node* pos = _root;
    BST_Node* parent = nullptr;
    //寻找目标节点
    while (pos)
    {
      if (key < pos->_key) {
        parent = pos;
        pos = pos->_left;
      }
      else if (key > pos->_key) {
        parent = pos;
        pos = pos->_right;
      } //找到目标节点
      else
      {
        /*
						 删除节点分三种情况：
						 1.需要删除的节点的子树数量为 0
						 2.需要删除的节点的子树数量为 1
						 3.需要删除的节点的子树数量为 2
						 对于前两种情况，将子树移交给目标节点的父节点；
						 对于第三种情况，寻找合适的临时节点替代目标节点，并删除临时节点
						*/
        if (pos->_left == nullptr)
        {
          //目标位置为根节点的情况需要独自处理
          if (pos == _root) {
            _root = pos->_right;
          }
          else
          {
            if (pos == parent->_left) {
              parent->_left = pos->_right;
            }
            else {
              parent->_right = pos->_right;
            }
          }
        }
        else if (pos->_right == nullptr)
        {
          if (pos == _root) {
            _root = pos->_left;
          }
          else
          {
            if (pos == parent->_left) {
              parent->_left = pos->_left;
            }
            else {
              parent->_right = pos->_left;
            }
          }
        }
        else
        {
          BST_Node* cur = pos->_left;
          BST_Node* parent = cur;
          //寻找目标节点的左子树的最右节点，以此节点作为临时节点
          while (cur->_right) {
            parent = cur;
            cur = cur->_right;
          }
          //交换节点的键值对以进行替换
          std::swap(cur->_key, pos->_key);
          std::swap(cur->_val, pos->_val);
          //删除临时节点
          //此处依然需要进行一次判断，因为不确定临时节点的位置
          //临时虽然是左子树的最右节点，但是并非一定是其父节点的右孩子
          if (cur->_left == nullptr)
          {
            if (cur == parent->_left) {
              parent->_left = cur->_right;
            }
            else {
              parent->_right = cur->_right;
            }
          }
          else
          {
            if (cur == parent->_left) {
              parent->_left = cur->_left;
            }
            else {
              parent->_right = cur->_left;
            }
          }
        }
        return true;
      }
    }
    return false;
  }

  BST_Node* Find(const Key& key) const
  {
    BST_Node* cur = _root;
    //根据二叉搜索树的性质进行搜索
    while (cur)
    {
      if (key < cur->_key) {
        cur = cur->_left;
      }
      else if (key > cur->_key) {
        cur = cur->_right;
      }
      else {
        return cur;
      }
    }
    return nullptr;
  }

  bool Empty() const
  {
    return _root == nullptr;
  }

  void InOrder() const
  {
    _InOrder(_root);
  }

  private:
  BST_Node* _copyConstruct(BST_Node* BSTreeRoot)
  {
    if (BSTreeRoot == nullptr) {
      return nullptr;
    }

    BST_Node* root = new BST_Node(BSTreeRoot->_key, BSTreeRoot->_val);
    root->_left = _copyConstruct(BSTreeRoot->_left);
    root->_right = _copyConstruct(BSTreeRoot->_right);

    return root;
  }

  void Destroy(BST_Node* root)
  {
    if (root == nullptr) {
      return;
    }

    Destroy(root->_left);
    Destroy(root->_right);
    delete root;
    root = nullptr;
  }
  
  void _InOrder(const BST_Node* root) const
  {
    if (root == nullptr) {
      return;
    }
    _InOrder(root->_left);
    cout << root->_val << ' ';
    _InOrder(root->_right);
  }

  private:
  BST_Node* _root;
};

递归方式实现

template<typename Key, typename Value>
struct BinarySearchTreeNode
{
  typedef BinarySearchTreeNode<Key, Value> BST_Node;

  BinarySearchTreeNode<Key, Value>(const Key& k, const Value& v)
    :_key(k), _val(v),
  _left(nullptr), _right(nullptr)
  { }

  Key _key;
  Value _val;
  BST_Node* _left;
  BST_Node* _right;
};

template<typename Key, typename Value>
class BinarySearchTree
{
  private:
  typedef BinarySearchTreeNode<Key, Value> BST_Node;

public:
  BinarySearchTree()
    :_root(nullptr)
    { }

    ~BinarySearchTree()
    {
      Destroy(_root);
    }
		//下面的接口都在子函数中进行递归调用
    bool Insert(const Key& key, const Value& val)
    {
      return _insert(key, val, _root);
    }

    bool Erase(const Key& key)
    {
      return _erase(key, _root);
    }

    BST_Node* Find(const Key& key) const
    {
      return _find(key, _root);
    }

    bool Empty() const
    {
      return _root == nullptr;
    }

    void InOrder() const
    {
      _InOrder(_root);
    }

private:
  //使用root指针的引用，使root与上层栈帧的指针保持关联，便于节点的链接
  bool _erase(const Key& key, BST_Node*& root)
  {
    if (root == nullptr) {
      return false;
    }

    if (key < root->_key) {
      return _erase(key, root->_left);
    }
    else if (key > root->_key) {
      return _erase(key, root->_right);
    }
    else
    {
      BST_Node* delNode = root;
      if (root->_left == nullptr) {
        root = root->_right;
        delete delNode;
      }
      else if (root->_right == nullptr) {
        root = root->_left;
        delete delNode;
      }
      else
      {
        //寻找左子树的最大节点
        BST_Node* leftMax = root->_left;
        while(leftMax->_right) {
          leftMax = leftMax->_right;
        }
        std::swap(leftMax->_key, root->_key);
        std::swap(leftMax->_val, root->_val);

        //此处可以直接递归删除关键码为key临时节点
        return _erase(key, root->_left);
      }
      return true;
    }
  }

  //使用root指针的引用，使root与上层栈帧的指针保持关联，便于节点的链接
  bool _insert(const Key& key, const Value& val, BST_Node*& root)
  {
    if (root == nullptr)
    {
      root = new BST_Node(key, val);
      return true;
    }

    if (key < root->_key) {
      return _insert(key, val, root->_left);
    }
    else if (key > root->_key) {
      return _insert(key, val, root->_right);
    }
    else if (key == root->_key) {
      return false;
    }
  }

  BST_Node* _find(const Key& key, BST_Node* root) const
  {
    if (root == nullptr || key == root->_key) {
      return root;
    }
    //任意子树找到即返回
    BST_Node* ret_left = _find(key, root->_left);
    if (ret_left) {
      return ret_left;
    }
    BST_Node* ret_right = _find(key, root->_right);
    if (ret_right) {
      return ret_right;
    }
  }

  void Destroy(BST_Node* root)
  {
    if (root == nullptr) {
      return;
    }

    Destroy(root->_left);
    Destroy(root->_right);
    delete root;
    root = nullptr;
  }

  void _InOrder(const BST_Node* root) const
  {
    if (root == nullptr) {
      return;
    }
				_InOrder(root->_left);
				cout << root->_val << ' ';
				_InOrder(root->_right);
  }

  private:
  BST_Node* _root;
};

二叉搜索树实现细节

无论是迭代写法还是递归写法，二叉搜索树的erase()接口都相对麻烦，需要分三种情况进行考虑(如上面代码中的注释所述)。在转交子树和删除结点的过程中，要全面地考虑节点可能的分布情况，若一欲贪图方便就会产生意料不到的问题。例如删除具有两棵子树的节点，最后删除临时节点时依旧需要判断临时节点的位置。