看一些分布式相关的技术文章或书籍时,经常看到一个词,一致性哈希。对于这个技术一直似懂非懂。今天花了半天的时间好好研究了它的原理和实现,发现一点都不复杂。于是写篇文章分享一下。
下面,我们就从基本的Hash算法说起。
负载均衡与Hash算法
分布式系统中(如:web存储),当服务增长到一定规模时,惯常的做法是集群化,引入负载均衡,这样做的好处是:1. 高可用。2. 解耦。从外部看,透明化了集群的内部细节(外部都通过负载均衡服务器通信,然后由负载均衡服务器分发请求)。
假设一个简单的场景:有4个cache服务器(后简称cache)组成的集群,当一个对象object传入集群时,这个对象应该存储在哪一个cache里呢?一种简单的方法是使用映射公式:
Hash(object) % 4这个算法就可以保证任何object都会尽可能随机落在其中一个cache中。一切运行正常。
然后考虑以下情况:
- 由于流量增大,需要增加一台cache,共5个cache。这时,映射公式就变成
Hash(object) % 5。 - 有一个cache服务器down掉,变成3个cache。这时,映射公式就变成
Hash(object) % 3。
可见,无论新增还是减少节点,都会改变映射公式,而由于映射公式改变,几乎所有的object都会被映射到新的cache中,这意味着一时间所有的缓存全部失效。 大量的数据请求落在app层甚至是db层上,这对服务器的影响当然是灾难性的。
这时,我们就需要新的算法。
一致性Hash
一致性hash的出现就是为了解决这个问题:当节点数量改变时,能够使失效的缓存数量尽可能少。
一致性Hash的基本思想就是分两步走:
- 把object求hash(这一步和之前相同);
- 把cache也求hash,然后把object和cache的hash值放入一个hash空间,通过一定的规则决定每个object落在哪一个cache中。
下面,会逐步说明它的实现。
成环
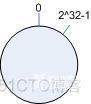
考虑通常的Hash算法都是将value映射到一个32位的key值,也即是0 ~ 2 ^ 32 - 1次方的数值空间;我们可以将这个空间想象成一个首(0)尾(2 ^ 32 - 1)相接的圆环,如下图所示。
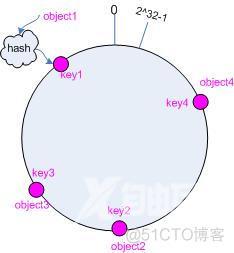
将object映射到环上
比如有4个需要存储的object,先求出它们的hash值,根据hash值映射到环上。如图:
将cache映射到环上
假设有三台cache服务器:cache A,cache B,cache C。用同样的方法求出hash值(可根据机器的IP或名字作为key求hash,只要保证hash值足够分散),映射到同一个环上。如图:
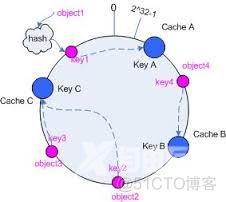
将object按照规则配对cache
这里的规则很简单:让object在环上顺时针转动,遇到的第一个cache即为对应的cache服务器。
根据上面的方法,对object1将被存储到cache A上;object2和object3对应到cache C;object4对应到cache B。
解决问题
新的一致性hash算法成功解决了cache服务器增减时key的失效问题。现在,无论增减cache,只有部分key失效。
考虑增加新的缓存服务器的情况:
如图,新增了cache D节点,假设cache D在环上落在C和A之间,那么失效的只有部分落在cache A的key(现在落在cache D了);也就是部分的红色圆弧,变成橙色圆弧(D)。
而cache B和cache C的key都没有失效。
可见,在新增节点时,这已经是最少失效了。
在移除节点时,情况也是和新增节点类似的。
虚拟节点
hash算法的一个考量指标是平衡性。在本例中,我们希望每一个object落在任意一个cache的机会都尽可能接近。
从图上很容易直观的看到,对于一个object来说,它落在环上的任何位置的概率都是一样的,那么落在一个cache的概率就和圆弧的长度成正比。于是,我们希望每个cache所占的圆弧长度更接近。
其实,理论上,只要cache足够多,每个cache在圆环上就会足够分散。但是在真实场景里,cache服务器只会有很少,所以,引入了“虚拟节点”(virtual node)的概念:
以仅部署cache A和cache C的情况为例,引入虚拟节点,cache A1, cache A2代表了cache A;cache C1,cache C2代表了cache C。
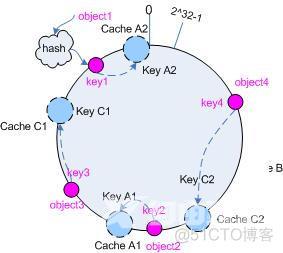
此时,对象到“虚拟节点”的映射关系为:
objec1->cache A2;objec2->cache A1;objec3->cache C1;objec4->cache C2;
因此对象object1和object2都被映射到了cache A上,而object3和object4映射到了cache C上;平衡性有了很大提高。
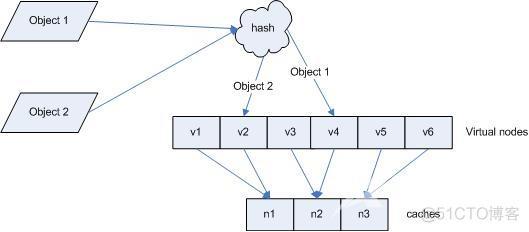
虚拟节点技术实则是做了两次matching,如图: