二叉树
104. 二叉树的最大深度
题意:给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:

思路:两种思路:1.递归法:利用后序遍历左右中的思路,计算根节点的左右子树高度那个最大,找出最大的深度;2.回溯法:定义一个最大深度maxTmp,然后让maxNum模拟回溯思想,每次循环都要判断是否刷新最大深度,并且,这里需要注意:此时的递归结束条件是判断到叶子节点的末尾,因此我们需要在每次判断条件之前进行最大深度的更新,而递归法的终止条件是遍历的位置为空节点返回,该层不算作最大深度,因此要在终止条件后进行最大深度的更新。
递归法:
int maxDepth(TreeNode* root) {
if(nullptr==root)//递归终止条件,节点为空,表示没有层数可以加
{
return 0;
}
int leftNum=maxDepth(root->left);//左子树的高度
int rightNum=maxDepth(root->right);//右子树的高度
int maxNum=1+max(leftNum,rightNum);
return maxNum;
}回溯法:
int maxTmp = 0;//最大深度
void maxDep(TreeNode* root, int& maxNum)
{
if (maxTmp<maxNum)//这里需要提前判断,因为终止条件会忽略叶子节点的层数
{
maxTmp = maxNum;
}
if (nullptr == root->left&&nullptr == root->right)//判断到叶子节点,返回
{
return;
}
if (root->left)//回溯模拟递归
{
maxNum++;
maxDep(root->left, maxNum);
maxNum--;
}
if (root->right)
{
maxNum++;
maxDep(root->right, maxNum);
maxNum--;
}
}
int maxDepth(TreeNode* root) {
if (nullptr == root)//先判断树是否为空,不为空,再去开辟空间计算最高层
{
return 0;
}
int maxNum = 1;
maxDep(root, maxNum);
return maxTmp;
}111. 二叉树的最小深度
题意:给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例:

思路:本题我们需要注意,什么是符合条件的最小深度?即该节点必须有左右子树的情况,若有一边没有子树,则该树的最小深度必定在另一边+1。因此,我们可以从上题中的代码增加一个判断选项,若没有左子树,只有右子树,返回右子树最小深度+1;若没有右子树,只有左子树,返回左子树最小深度+1;若都有,则正常判断二叉树最小深度
递归法:
int minDepth(TreeNode* root) {
if(nullptr==root)
{
return 0;
}
int leftNum=minDepth(root->left);//这里我们会计算出左右子树的高度
int rightNum=minDepth(root->right);
if(nullptr==root->left&&root->right)//特殊情况,这里的最小深度是子树的,若没有子树,则只能为另一边的深度
{
return 1+rightNum;
}
if(nullptr==root->right&&root->left)
{
return 1+leftNum;
}
int minNum=1+min(leftNum,rightNum);//左右子树都有,那就是正常的左右子树高度判断
return minNum;
}222. 完全二叉树的节点个数
题意:给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例:
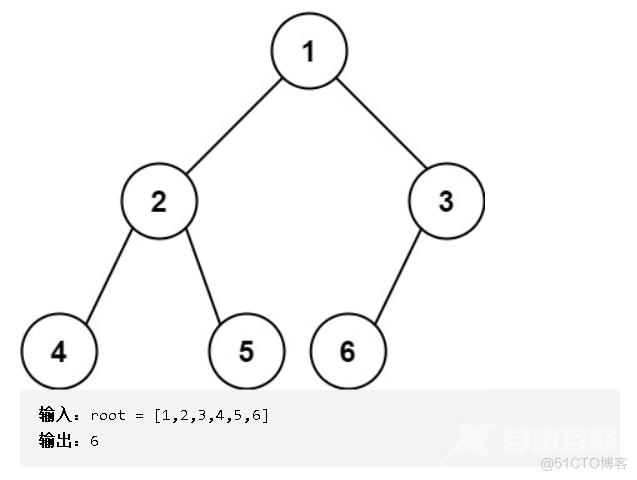
思路:本题还是分为两种思路:1.递归法:将每次的左右子树节点记录下来,每次+1即可,思路非常简单 2.迭代法:我认为该种方法更像是队列的思路,迭代有点抽象,我们先判断树是否为空,为空,直接返回0,就不需要开辟额外空间了;不为空,需要开辟一个队列,然后放入第一个节点(根节点),仿照广度有限遍历的思想,一个一个剔除节点,再从剔除的节点中添加节点即可,最终,当队列中没有节点时,说明遍历完毕
递归法:
int countNodes(TreeNode* root) {
if(nullptr==root)
{
return 0;
}
int leftNum=countNodes(root->left);
int rightNum=countNodes(root->right);
int count=leftNum+rightNum+1;
return count;
}迭代法:
int countNodes(TreeNode* root) {
if(nullptr==root)//先判断是否为空,不为空才有之后开辟空间的必要
{
return 0;
}
queue<TreeNode*> q;//先将根节点写入
q.push(root);
int count=0;
while(!q.empty())//循环剔除节点
{
TreeNode* cur=q.front();
if(cur->left)//只有该节点有子节点时,才放入
{
q.push(cur->left);
}
if(cur->right)
{
q.push(cur->right);
}
count++;
q.pop();//一次循环只计算一个节点,计算的速度由快到慢再到快
}
return count;
}