【LeetCode】35.搜索插入位置

35.搜索插入位置

分析：target一共有以下几种情况：

1.target等于数组中某一个元素；

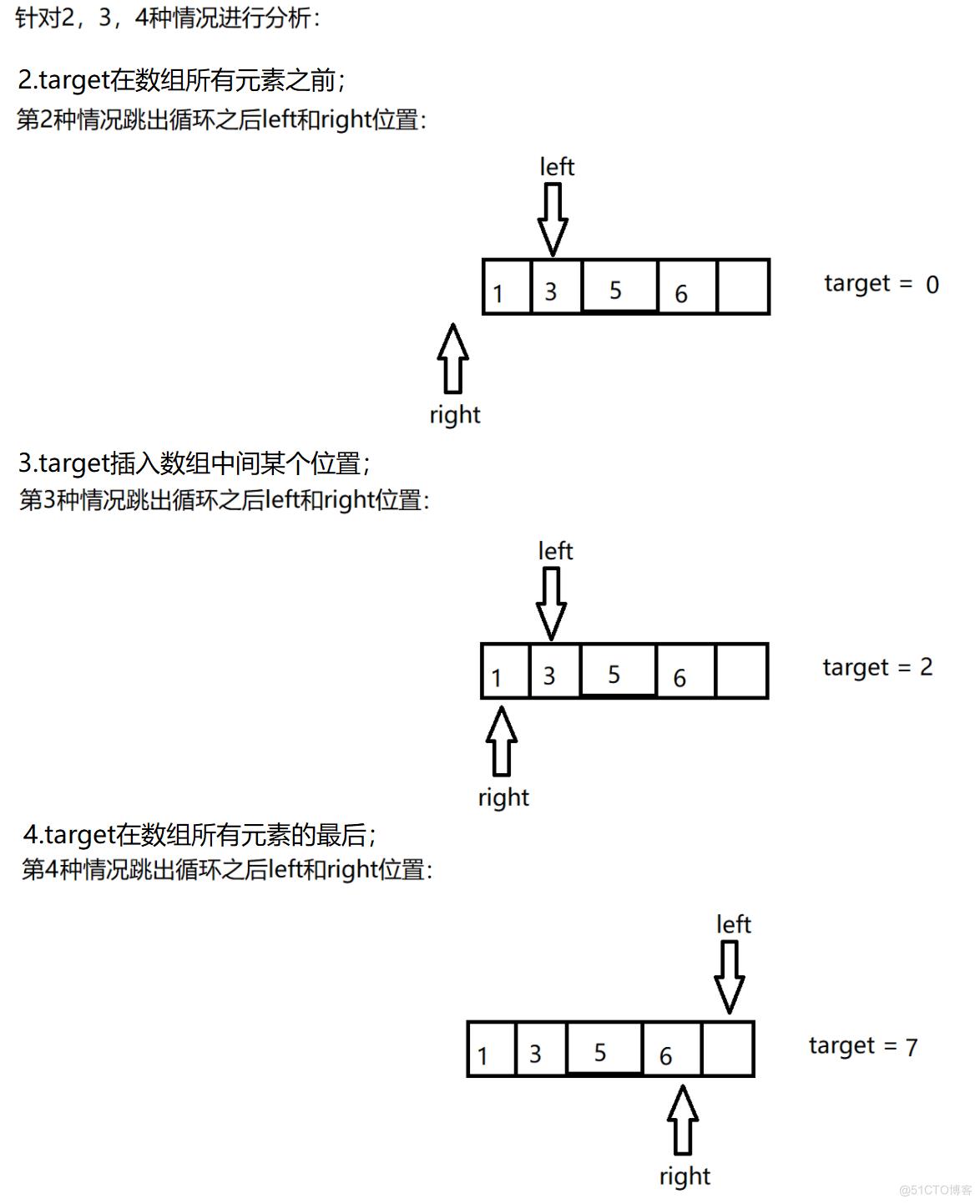
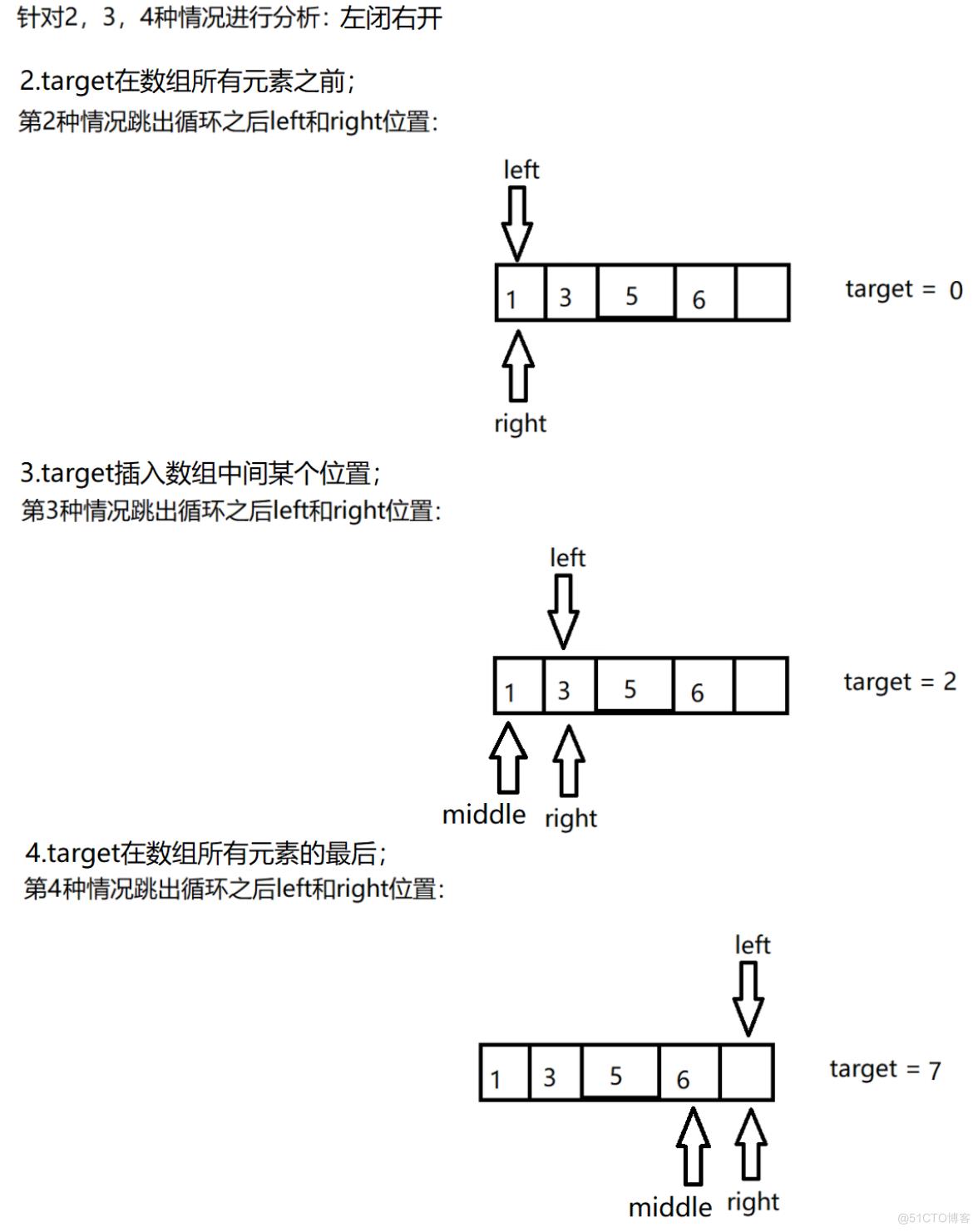
2.target在数组所有元素之前；

3.target插入数组中间某个位置；

4.target在数组所有元素的最后；

思路一：暴力解法

nums 为无重复元素的升序排列数组，所以我们可以通过nums[i] >= target处理前三种情况；最后一种情况直接使用return nums.size()。时间复杂度：O(N)，空间复杂度：O(1)。

代码如下：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        for(int i = 0; i < nums.size(); i++)
        {
            //nums 为无重复元素的升序排列数组
            //所以我们可以处理下面的情况：
            //1.target等于数组中某一个元素；
            //2.target在数组所有元素之前；
            //3.target插入数组中间某个位置；

            //因为是升序所以当大于或者等于的时候就返回i
            if(nums[i] >= target) 
                return i;
        }
        //4.target在数组所有元素的最后；
        return nums.size(); //所有元素的最后就是数组长度
    }
};

思路二：二分查找

二分查找使用前提条件：有序数组且无重复元素。

先使用二分查找处理target等于数组中某一个元素位置，然后再通过right处理剩下的情况。

左闭右闭代码：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int right = nums.size() - 1;
        int left = 0;
        
        //1.处理target等于数组中某一个元素位置
        while(left <= right) //[left,right],while条件合法
        {
            int middle = left + ((right - left) / 2);//防止溢出 等同于(left + right)/2
            if(nums[middle] > target)
                right = middle - 1;//target比nums[middle]小，在左区间，更新右边界
            else if(nums[middle] < target)
                left = middle + 1;//target比nums[middle]大，在右区间，更新左边界
            else // nums[middle] == target
                return middle;
        }

        //处理下面的情况：
        //2.target在数组所有元素之前；
        //3.target插入数组中间某个位置；
        //4.target在数组所有元素的最后；
        return right + 1;
    }
};

左闭右开代码：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int right = nums.size();
        int left = 0;

        //1.处理target等于数组中某一个元素位置
        while(left < right) //[left,right),while条件合法
        {
            int middle = left + ((right - left) >> 1);//防止溢出 等同于(left + right)/2
            if(nums[middle] > target)
                right = middle;//target比nums[middle]小，在左区间，更新右边界，
            else if(nums[middle] < target)
                left = middle + 1;//target比nums[middle]大，在右区间，更新左边界
            else // nums[middle] == target
                return middle;
        }

        //处理下面的情况：
        //2.target在数组所有元素之前；
        //3.target插入数组中间某个位置；
        //4.target在数组所有元素的最后；
        return right;
    }
};