运用数组来完成循环队列

题目：

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k 。
• Front: 从队首获取元素。如果队列为空，返回 -1 。
• Rear: 获取队尾元素。如果队列为空，返回 -1 。
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
• isEmpty(): 检查循环队列是否为空。
• isFull(): 检查循环队列是否已满。

解题思路

这道题我们可以使用数组来完成循环队列也可以使用链表来完成循环队列

若我们使用的树组来实现我们要创建三个变量，变量1用于储存初始位置，变量2用于储存要插入的数据的位置，如果要增加数据了，就让变量2的位置先增加数据，再让变量2自增。若要删除数据则让变量1自增就可以了。还有一个变量用于储存循环队列能放入的数据个数。

下面我们通过画图来理解这种方式

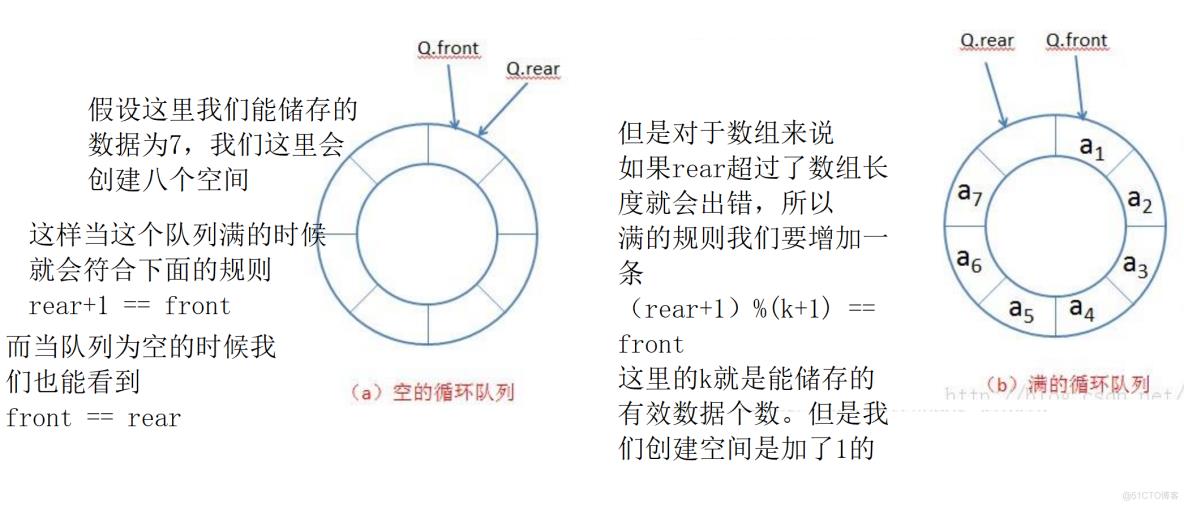
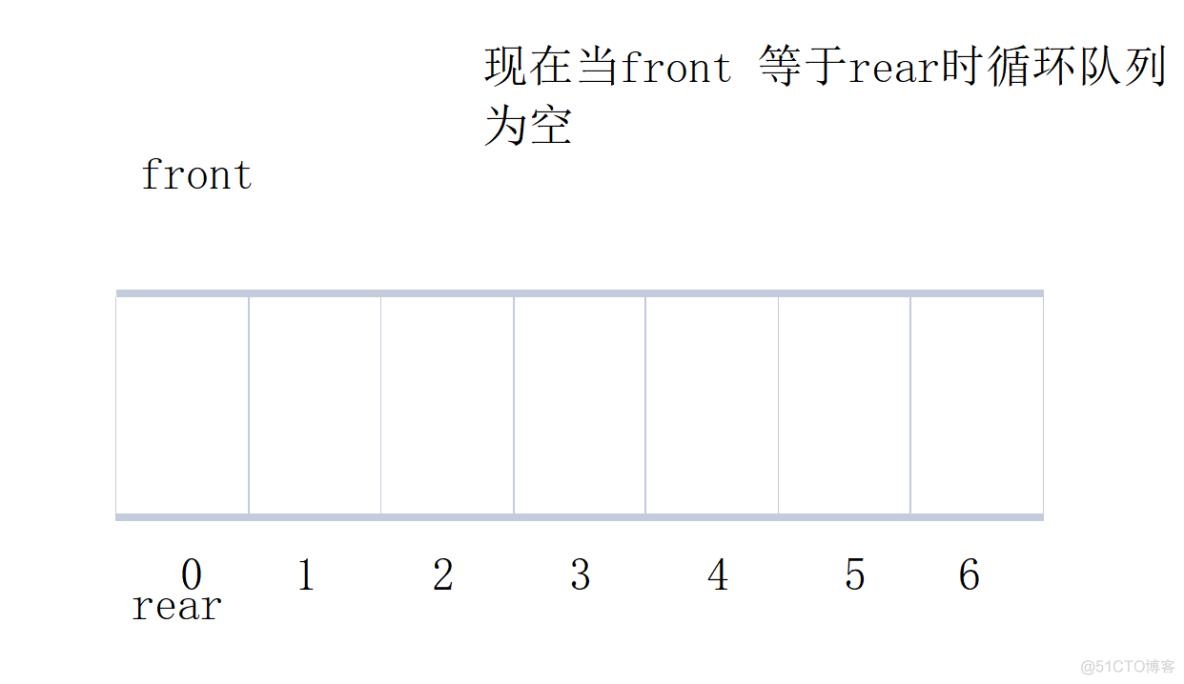
对于小于有效数据个数+1的rear来说模上一个有效个数+1对于自身是而没有任何影响的。

而当大于时模就能让其返回0到有效的下标，即一个数模上x（x若等于5）则得到的值范围在0到4.

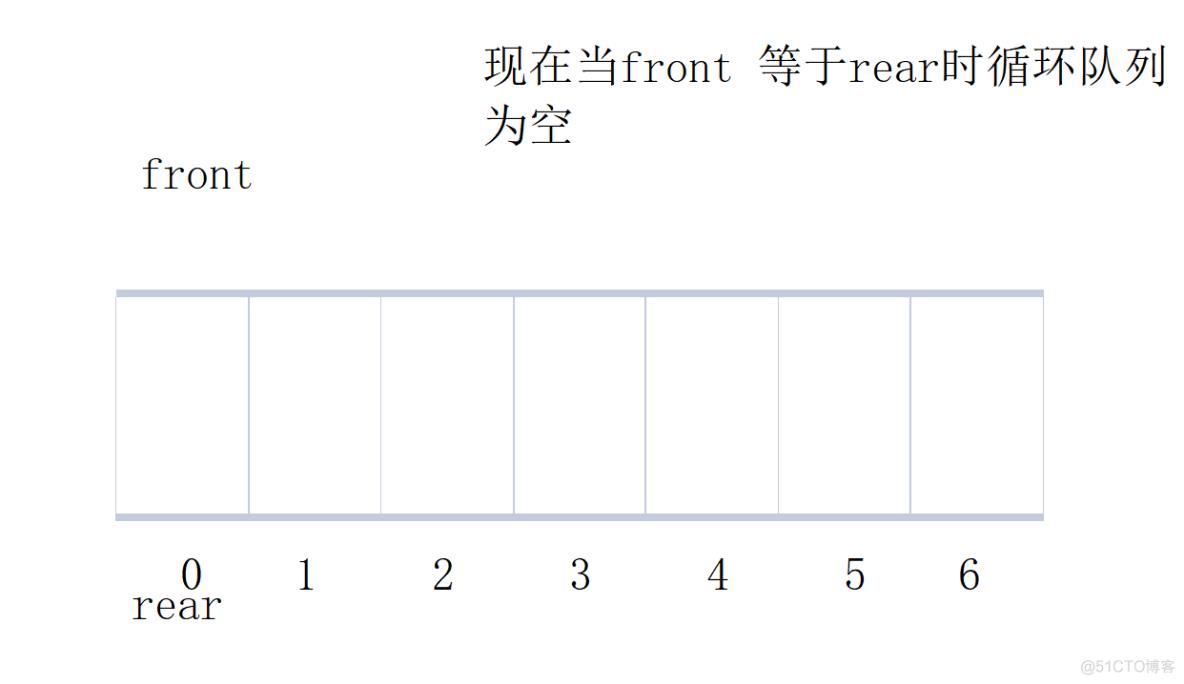
最后题目还要求我们能够返回头数据和尾数据，头数据很容易就能返回但是尾数据却要分情况，因为我们的rear指向的是尾数据的下一个数据，所以为数据应该是rear-1，但是如果遇到下图中的情况又要怎么办呢？

下面我们就来写题：

typedef struct 
{
    int front;//记录头
    int rear;//记录尾
    int* a;//数组
    int k;//用以储存有效数据的个数

} MyCircularQueue;
bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front == obj->rear;//如果rear等于front代表队列为空
}

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return ((obj->rear+1)%(obj->k+1) == obj->front);
}

MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->front = 0;
    obj->rear = 0;
    if(obj == NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    //下面我们要为数组创建空间
    obj->a= (int*)malloc(sizeof(int)*(k+1));
    obj->k = k;
    return obj;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
    return false;//如果这个循环队列已经满了直接返回false

    obj->a[obj->rear] = value;
    obj->rear++;
    obj->rear%=(obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    return false;//如果队列已经空了，则返回false
    
    //如果没有空得话直接让front++即可达成删除效果
    obj->front++;
    obj->front%=(obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) 
{
     if(myCircularQueueIsEmpty(obj))
    return -1;//如果队列为空了按照要求返回-1

    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    return -1;

    return obj->a[(obj->rear+obj->k)%(obj->k+1)];

}



void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}

/**
 * Your MyCircularQueue struct will be instantiated and called as such:
 * MyCircularQueue* obj = myCircularQueueCreate(k);
 * bool param_1 = myCircularQueueEnQueue(obj, value);
 
 * bool param_2 = myCircularQueueDeQueue(obj);
 
 * int param_3 = myCircularQueueFront(obj);
 
 * int param_4 = myCircularQueueRear(obj);
 
 * bool param_5 = myCircularQueueIsEmpty(obj);
 
 * bool param_6 = myCircularQueueIsFull(obj);
 
 * myCircularQueueFree(obj);
*/