n-皇后问题是一个经典的dfs深度优先遍历的题目,在题解这一题之前,将由浅入深,先讲解一个n-皇后问题的母题。-------AcWing 842. 排列数字
[AcWing 842]. 排列数字
题目概述
给定一个整数 n,将数字 1∼n排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
3输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1题解思路:
重要的是搜索顺序,用什么样的顺序进行遍历,观察数据发现,没有重复的,说明在遍历搜索的时候是要标记那些是被选过,哪一些没有被选过的,当我选出的数需要放到一个数组里面,当长度和n相等说明这个选出的所有数就是一个排列,直接输出。下图就是算法递归过程中往下找和往上回溯的过程图:
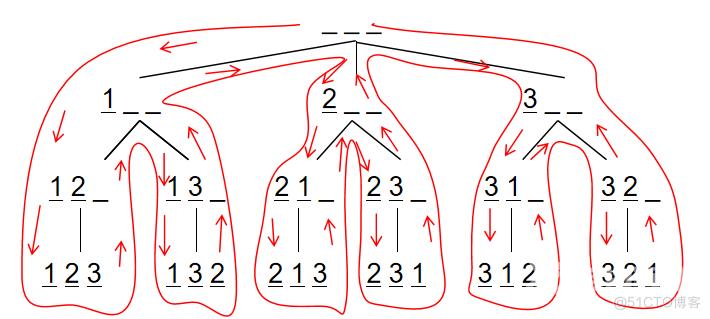
算法:
- 用 val 数组保存排列,当排列的长度为 n 时,是一种方案,输出。
- 用 state 数组表示数字是否用过。当 state[i] 为 1 时:i 已经被用过,state[i] 为 0 时,i 没有被用过。
- dfs(i) 表示的含义是:在 val[i] 处填写数字,然后递归的在下一个位置填写数字。
- 回溯:第 i 个位置填写某个数字的所有情况都遍历后, 第 i 个位置填写下一个数字。
代码:
#include<iostream>
using namespace std;
int n;
const int N=10;
int val[N]; //用来存选的数
int state[N]; //标记状态
void dfs(int u)
{
if(u>n)
{
for(int i=1;i<=n;i++)
{
cout<<val[i]<<" ";
}
cout<<endl;
}
for(int i=1;i<=n;i++) //从1~n中选数字
{
if(!state[i]) //没被选过的进入
{
val[u]=i; //在u位置放i
state[i]=1;
dfs(u+1);
state[i]=0; //回溯 到了dfs下一个 i是没有被选过的得还原
}
}
}
int main()
{
cin>>n;
dfs(1);
}输出结果:
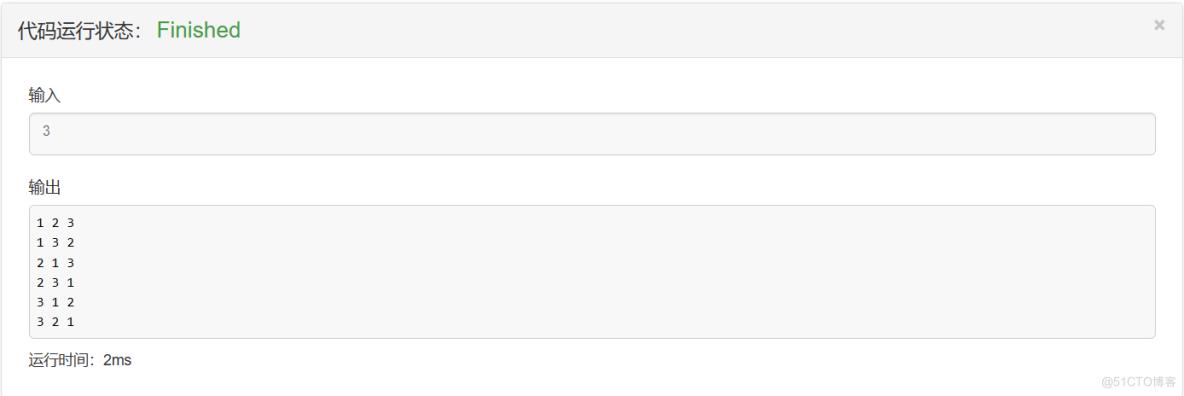
[AcWing] 843. n-皇后问题
这个问题是上面排列数字的升级版,模板也是一样,上一题是要满足不能重复出现的排列,n皇后就是在同行、同列、正反对角线都不能有皇后的组合方案。
题目概述
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互打到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
题解思路:
核心解题思路和排列数字相似,用一个数组来存整个棋盘,需要满足行列正反对角线都不能有皇后,所以也设置标志数组true、false来进行判断是否有皇后。当dfs(u)的u==n,那么就是相当于找到了一组解,那么就输出出来,如果标志数组发现没有皇后,那么把Q放进存储数组,然后标志数组进行更新为true。接着递归u+1,一定要注意是回溯回去之后要把存储数组这个给还原,目前是我递归进来的,我在这个状态下是被设置为皇后Q,当我递归开始回溯后,回到我当前状态的上一个状态我还是'.',所以要还原。
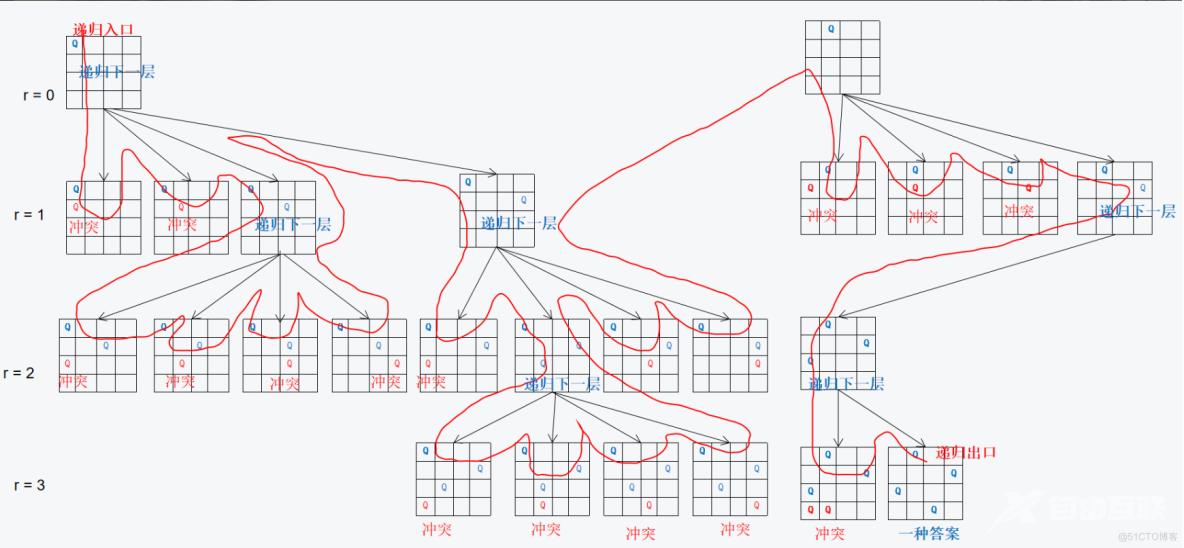
算法:
- 用 arr数组保存棋盘,当dfs(u)的长度为 n 时,是一种方案,输出。
- 用 col[N] dg[N] udg[N] 数组表示这个位置是否有皇后。当 col[N]&& dg[N]&& udg[N] 为true ,那么这个位置的行还有正反对角线是存在皇后的, 为false ,那么这个位置的行还有正反对角线没有皇后可以放。
- dfs(i) 表示的含义是:在 arr[i] 处填写放皇后Q,然后递归的在下一个位置填写下个皇后Q。
- 回溯:第 i 个位置放皇后的所有情况都遍历后, 第 i 个位置填写下一个皇后。就得恢复现场,恢复到我上一个状态的时候是啥。
代码:
#include<iostream>
using namespace std;
int n;
const int N=20;
char arr[N][N]; // 放数据,用于存储棋盘
bool col[N],dg[N],udg[N]; // 限制行、正对角线、反对角线
void dfs(int u) // 搜索函数,参数u表示当前处理到第几行
{
if(u==n) // 当前处理到第n行,说明已经找到一组解,输出并返回
{
for(int i=0;i<n;i++) puts(arr[i]); // 输出棋盘的一种解
puts(""); // 换行
return;
}
for(int i=0;i<n;i++) // 枚举放在第u行的皇后的列号
{
if(!col[i]&&!dg[u+i]&&!udg[i-u+n]) // 判断这个位置是否可行
// 判断此列,正负对角线是否有另一枚皇后,如果没有则可以放置皇后
{
arr[u][i]='Q'; // 将这个位置放上皇后
col[i]=dg[i+u]=udg[i-u+n]=true; // 更新限制条件
dfs(u+1); // 继续搜索下一行
col[i]=dg[i+u]=udg[i-u+n]=false; // 回溯时要恢复限制条件
arr[u][i]='.'; // 回溯时要恢复棋盘状态
}
}
}
int main()
{
cin>>n; // 输入皇后数量
for(int i=0;i<n;i++) // 初始化棋盘,全部置为'.'表示无皇后
{
for(int j=0;j<n;j++)
{
arr[i][j]='.';
}
}
dfs(0); // 从第0行开始搜索
return 0;
}对对角线dg[u+i] 和udg[i-u+n]的理解:
以反对角线举例,i- u其实就是该点在对角线上的截距 由中学知识可知对角线方程为y = x + b,其中b表示截距也就是b = y - x(数组下标里面的东西),如果在不同行,但再同一对角线,经过方程计算得到的截距都是一样的,不懂就拿纸自己写一下,+n是为了防止负数产生, 因为数组下标是不可能为负数的,因为每个数都+n,他们映射到结果是一样的,不信你就换个比n大的数试试。
输出结果: