值得理解的链表oj题

题目1：力扣141题环形链表

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

例如下面的这个就是有环的链表

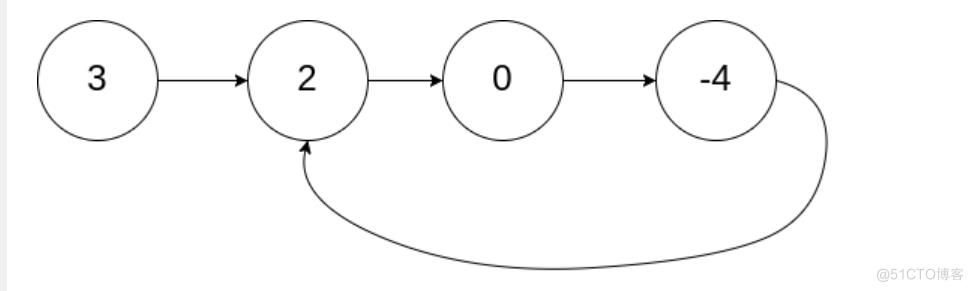
对于这种题最麻烦的一点就是我们不能遍历链表因为链表的遍历只会进入死循环，有几种思路可以写这种题目其中一种就是使用哈希表，但是因为我还未学习到哈希表就不写这种方式了。

那么还有一种方式也就是使用快慢指针，我们创建两个指向头节点的指针，同时让一个指针一次走两步一个指针一次走1步，如果这是一个有环的链表那么最后这两个指针会相等，我先将代码写出来之后再证明这个结论

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) 
{
    //首先创建两个快慢指针
    struct ListNode* fast = head,*slow = head;
    while(fast&&fast->next)//需要判断是否有环如果没有环的话快指针的next肯定会指向null
    {
         fast = fast->next->next;//快指针一次走两步
         slow = slow->next;//慢指针一次走一步
         if(fast == slow)
         return true;
    }
    return false;//如果快指针的next指向了NULL证明这不是一个有环的链表
}

141题方法原理证明

我们通过画图来证明：

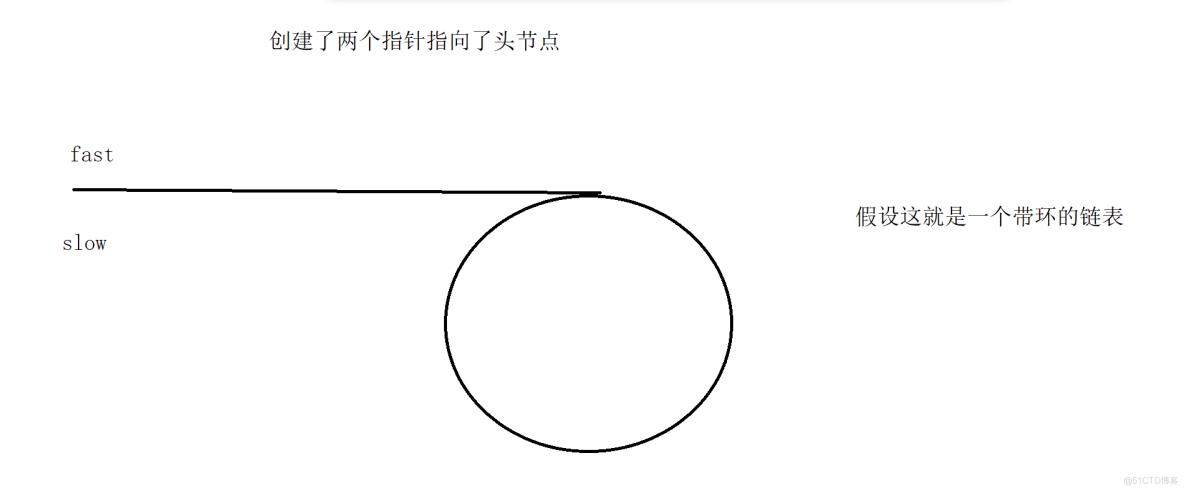
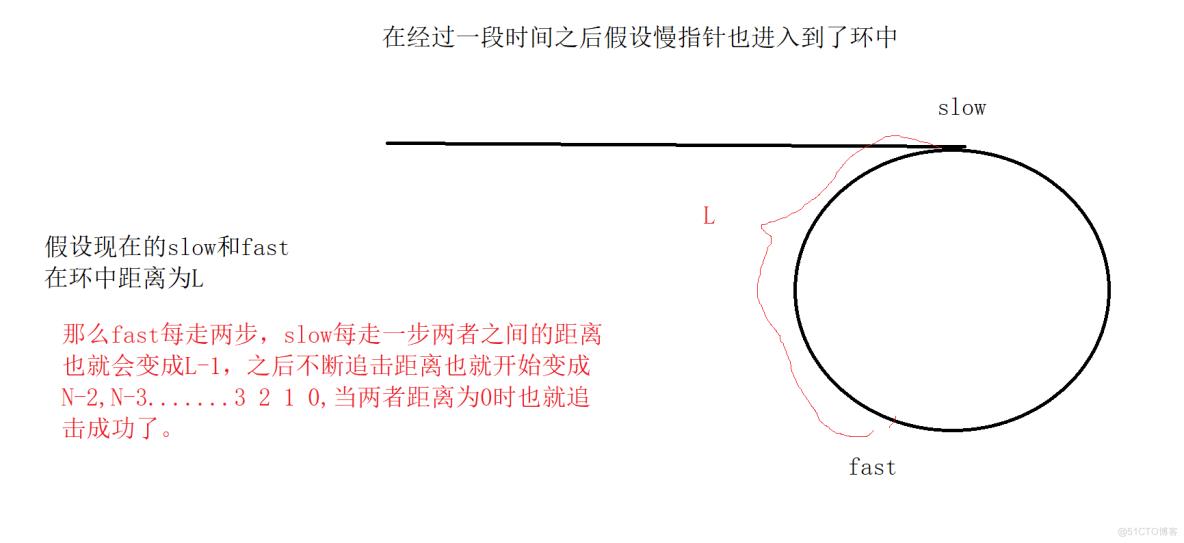
理解了这个原理之后我们再来看下面的两道题：

在fast只走两步，slow只走一步且存在环的情况下一定会相遇吗？

答案：很明显一定会相遇

能不能slow只走1步，而fast走n步（n>2）这种情况下一定会相遇吗？

答案：不一定。

我们假设fast走3步，那么当slow进入环中开始追击的时候两者之间的距离差也就变成了N-2，这时候能否相遇就取决于两者之间的距离是否为偶数，如果为偶数那么最后会相遇，如果为奇数则最后两者会错过，当错过后再次判断N是否为偶数，如果还是奇数则永远也不会相遇

题目二：力扣142题环形链表2

题目：给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

这道题和上面一道题一样都是先判断是否存在链表但是这道题最后要求你进入环形时的那个位置。

先写思路：思路就是我们在fast和slow相遇的那个位置和头节点的位置，都一起向前两者相同的那个位置也就是环的进口，

struct ListNode *detectCycle(struct ListNode *head) 
{
    //思路使用双指针，一个指针往前走两步一个指针往前走1步
    struct ListNode* fast = head;
    struct ListNode*  slow = head;
    while(fast&&fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            while(head != fast)
            {
                head = head->next;
                fast = fast->next;
            }
            return head;//使用的是结论，当确定一个链表有环之后
            //我们找到快慢节点相等的地方，再让一个新指针从头节点出发，当fast和这个新出发的指针相等
            //的时候也就找到了环形链表的出发点
            //这道题的难点依旧在于我们如何证明这个结论
        }
    }
    return NULL;   
}

142题方法原理证明

我们依旧是通过画图来证明

这是准备工作

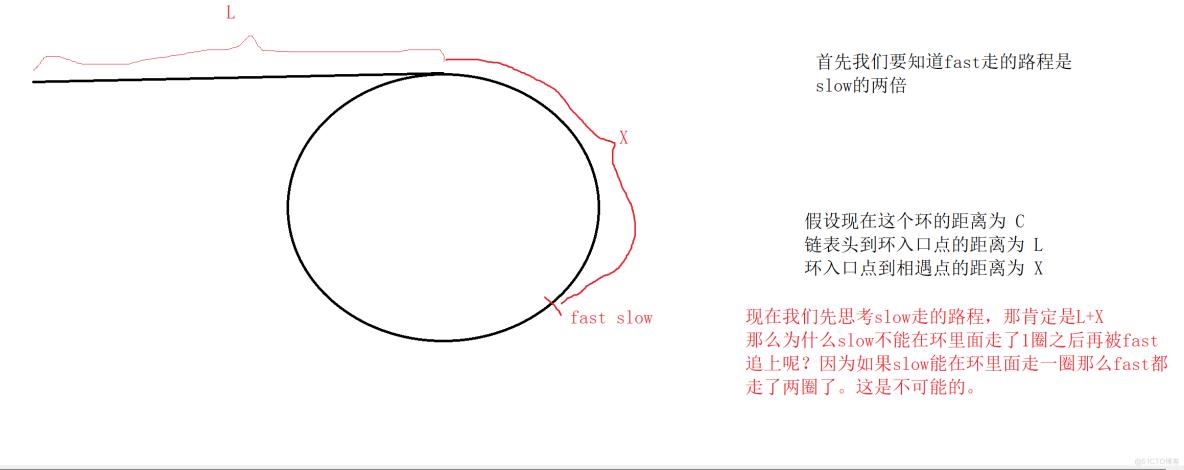
接下来

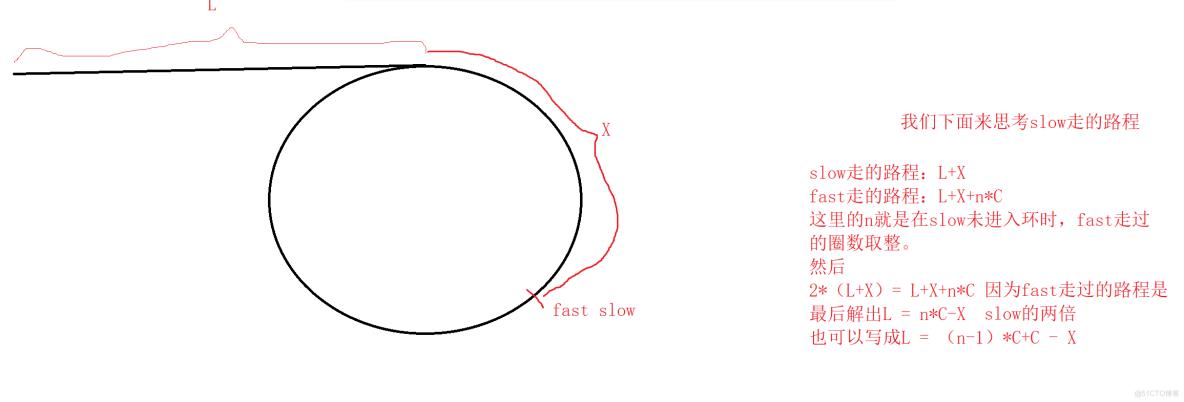
我们先来看L = n*C -X，我们可以想象一下当一个指针从链表头走到链表环的入口的时候，我们从相遇点开始前进的指针先是在环里面转了n圈后返回到相遇掉，之后-X就代表往后退回X的距离很惊奇居然回到了环的入口点。此时从头出发的指针恰好也在这。直接返回即可

我们再来看L = （n-1）*C +C -X,前面的(N-1)*C自然不用管也就是在环里面转了N-1圈而已，我们最后要理解的是C-X，C是环的长度减去X自然是上图里面没有被红线包围的部分，从相遇点走这么多的距离最后依旧是返回到了环的入口点。

希望这篇文章能对你有所帮助。