归并排序和计数排序

本篇文章与大家分享一些关于归并排序，计数排序的相关知识，与大家一起了解什么是归并排序，什么是计数排序，以及我们如何实现这两个排序。

首先，我们先讲讲归并排序。

归并排序

思路

要实现归并排序，首先，我们得了解它的一个排序逻辑，那归并排序的逻辑是什么呢？相信大家在学c语言时，都遇到过这样一道题，给你两个有序的数组，合并成一个有序的数组。以上这种合并两个有序数列成一个有序数列的方法，也就是归并的实现方法。那我们如何去将要排序数组变成两个有序的序列再进行合并呢？是将传过来的数组分成两部分，分别进行排序，然后，再进行合并吗？答案，是否定的。那归并排序是如何得到两个有序的序列，再进行合并呢？大家设想一下，如果我们将一个乱序的序列分为两个序列，再将这两个序列分别分割成两个序列，如此反复分割下去，我们就可以分出由一个数构成的序列，而一个数构成的序列不就是有序的吗？了解完归并排序的实现方法，接下来，让我们看看归并排序实现过程的动画。

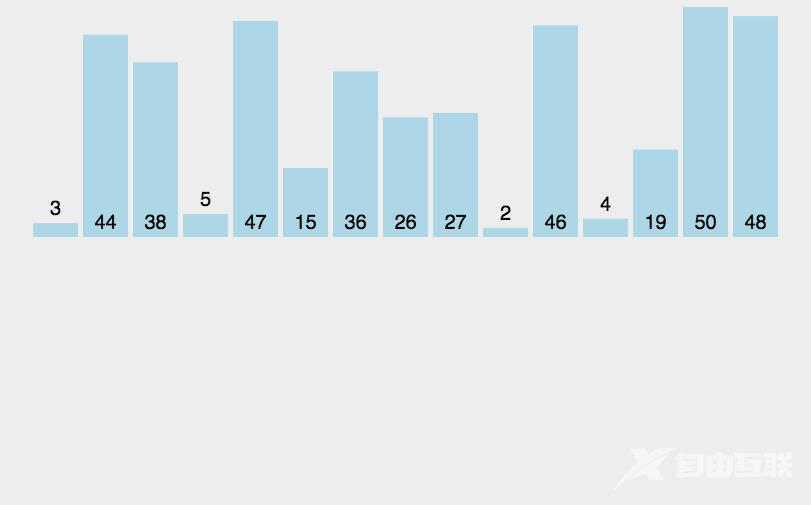
实现方法

了解完归并排序的实现方法，接下来，让我们用代码来实现它。

递归实现

//归并排序
void MergeSort(int* str, int n)
{
  //我们不能直接在原数组上直接进行合并排序，这样会将原有的数据覆盖掉，所以，
  //我们需要开辟一个空间来合并两个有序的序列。
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp)
	{
    //这里涉及到开辟空间，所以，我们不能直接用此函数进行递归，需要用到一个
    //子函数_Merge
		_Merge(str,0,n-1,tmp);
	}
	else
	{
		perror("malloc fail");
		return;
	}
  //空间使用完后，需要释放，避免内存的泄露
	free(tmp);
}

void _Merge(int* str, int begin, int end, int* tmp)
 {
  //当一个区域的起始位置大于末尾位置时，就没有需要合并的数据了，因此，我们
  //以此来做为递归的结束条件，那为什么等于也作为结束条件呢？你自己想一下，
  //等于意味指向同一个位置，而同一个位置就是同一个数，再怎么合并还是它本身。
	if (begin >= end)
		return;
  //接下来，我们需要不断地分割数组，得到两个有序的序列
	int mid = (end + begin) / 2;
	_Merge(str, begin, mid, tmp);
	_Merge(str, mid + 1, end, tmp);
  //到这里，我们已经获得了两个有序的序列，只需要将这两个有序的序列合并到
  //我们开辟的空间就行了
	int begin1 = begin;
	int begin2 = mid + 1;
	int end1 = mid;
	int end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (str[begin1] < str[begin2])
		{
			tmp[i++] = str[begin1++];
		}
		else
		{
			tmp[i++] = str[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = str[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = str[begin2++];
	}

  //此时，我们已经将两个有序的序列合并到了我们开辟空间中了，现在，我们只需将
  //得到的有序序列拷贝回原来的数组覆盖原有的数据就完成排序了。
	memcpy(str+begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

以上是递归的方式实现，让我们来看一下非递归的实现方法。

非递归实现

//归并排序非递归
//归并排序的非递归实现的思路与递归实现的思路一样，只是分割的方式改变了
void MergeSort(int* str, int n)
{
  //同样的开辟一个空间，用于合并两个有序序列
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp)
	{
		int gap = 1;
		while (gap < n)
		{
			int i = 0;
			int j = 0;
			for (j = 0;j < n;j += 2*gap)
			{
        //考虑两种情况，一是，begin2越界，也就是第二个有序序列不存在，只有
        //一个有序序列，不需要在进行合并。二是，begin2没越界，end2越界，
        //存在第二个有序序列，但范围错了，需要进行修改，将end2的值改为数组
        //末端
				int begin1 = j, end1 = j + gap-1;
				int begin2 = j + gap, end2 = j + 2 * gap - 1;
				if (n - 1 < begin2)
					break;
				if (n - 1 < end2)
					end2 = n - 1;
        //合并两个有序序列
				while (begin1 <= end1 && begin2 <= end2)
				{
					if (str[begin1] < str[begin2])
					{
						tmp[i++] = str[begin1++];
					}
					else
					{
						tmp[i++] = str[begin2++];
					}
				}

				while (begin1 <= end1)
				{
					tmp[i++] = str[begin1++];
				}

				while (begin2 <= end2)
				{
					tmp[i++] = str[begin2++];
				}
        //到这里，我们已经将合并后的序列放到了我们开辟的空间内了，只需要将
        //其拷贝回去就完成局部的排序了。
				memcpy(str + j, tmp + j, sizeof(int) * (end2 - j + 1));
			}
			gap*=2;
		}
	}
	else
	{
		perror("malloc fail");
		return;
	}
  //最后，就是释放我们开辟的空间了。
	free(tmp);
}

说到这里，或许你可能理解了归并排序，也可能没理解归并排序。不管，你属于哪种，都应该去试着实践一下，自己敲一下代码，或许，你现在想不通的，在实践中理解了。

回归正题，我们接下来了解一下计数排序。

计数排序

计数排序是一种不比较排序，它是如何实现的呢？让我们一起来看看它的实现思路。

思路

计数，计数就是计数，把每个出现的数出现的次数记录下来，然后，依次拷贝回原数组覆盖原有数据，就完成了排序。对于记录数据，我们需要开辟一个数组进行记录，比如说100就在数组100的位置进行加一。那数组开辟多少呢？根据数据不同大小，所需的开辟的空间也不同，所以，我们需要遍历一遍数据找出最小值和最大值。找最大值是为了确定开辟空间的大小，那找最小值是干啥的？我们设想一下，如果它给的数据是100到150之间的，我们开辟的空间是不是只有后面部分存储数据，前面的空间就造成了浪费，为此，我们引入了相对位置的概念，这样一来就减少了空间的浪费，以及负数记在那的问题。举个例子，假设最小值为5，有一个数据为10，那么我们以数组的起始位置为5，而它往后的第五个位置用来记录10；

接下来，让我们看一下代码的实现：

实现

//计数排序
void CountSort(int* str, int n)
{
	int i = n;
	int Min = str[0], Max = str[0];
	while (i--)
	{
		if (str[i] < Min)
			Min = str[i];
		if (str[i] > Max)
			Max = str[i];
	}
	int* tmp = (int*)calloc(Max-Min+1,sizeof(int));
	if (tmp == NULL)
	{
		perror("calloc fail");
		return;
	}
	for (i = 0;i < n;i++)
	{
		tmp[str[i] - Min]= tmp[str[i] - Min]+1;
	}
	int j = 0;
	for (i = 0,j=0;i < Max - Min + 1;i++)
	{
		if (tmp[i] > 0)
		{
			while (tmp[i]--)
				str[j++] = i + Min;
		}
	}
	free(tmp); 
}

好了，到这里，本次的分享就到此结束了，不知道我有没有说明白，给予你一点点收获。如果你有所收获，别忘了给我点个赞，这是对我最好的回馈，当然你也可以在评论发表一下你的收获和心得，亦或者指出我的不足之处。如果喜欢我的分享，别忘了给我点关注噢。