在这个项目中,我讨论了如何使用主成分分析 (PCA) 进行简单的预测。
出于说明目的,我们将对一个数据集进行分析,该数据集包含有关在 3 个不同价格组内进行的汽车购买信息以及影响其购买决定的一组特征。
首先,我们将导入数据集并探索其结构。
1.
2.
3. head(caref)


众所周知,PCA 使用欧几里得距离来推导分量,因此输入变量需要是数字的。正如我们所看到的,除了“组”变量之外,所有数据都是数字格式,因此我们不必执行任何转换。
为了查看数字变量在 3 个价格组中的表现,我分别为每个数字变量生成箱线图。
1. ggplot(cr_e.m, aes(x = varle, y = vle, fill = Gup)) +
2. geom_boxplot()
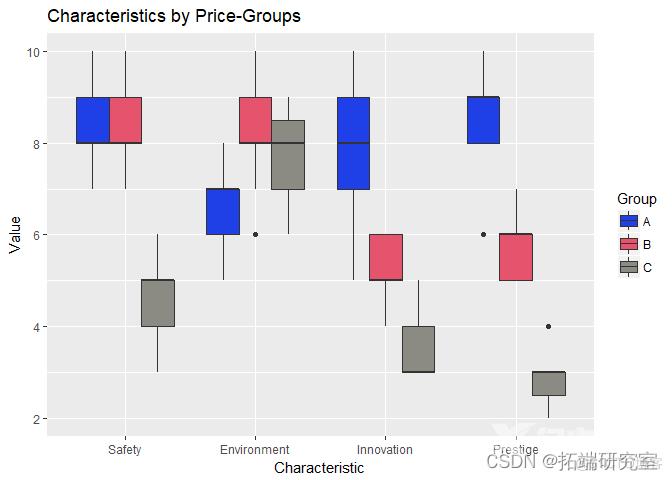
通过观察上图,我们可以了解到每个价格组的消费者对所考虑的特征有不同的看法(即,给出不同的评分)。(“安全”特征的变化较小,在所有 3 个价格组中具有更高的排名/重要性)
现在为了更好地可视化这 3 个价格组集群如何在 3D 空间中出现,我使用 3 个特征变量构建了一个 3D 图,显示给定评级之间的显着差异。
1.
2. same3dpot <- with(carpef, scttro3d(Enirnmnt,Innoaon,Prtge
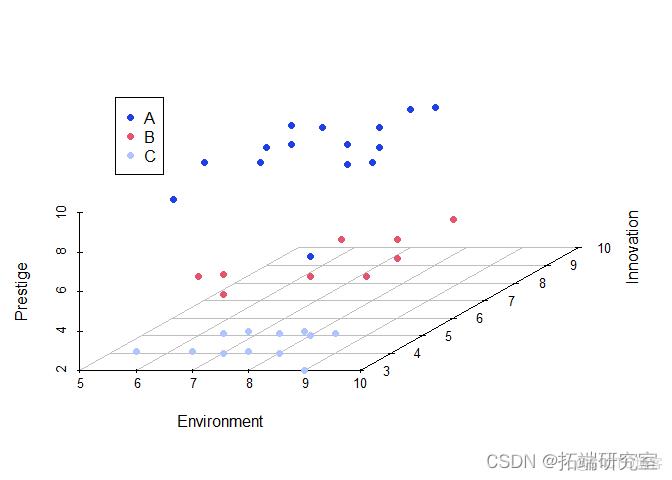
在上图中,我们可以看到来自每个价格组的数据点(集群)之间的明显差异。
在继续应用 PCA 之前,现在我将检查输入变量之间是否存在任何相关性。
1.
2. corrplot(oras)
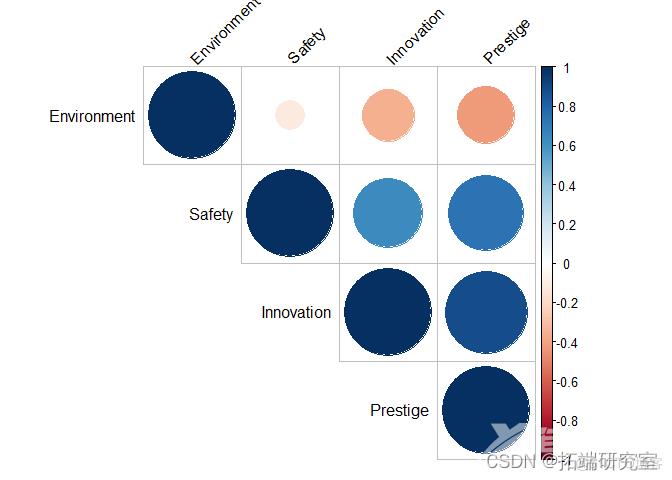
可以看出,“创新”、“安全”和“声望”特征之间似乎有明显的相关性。
通常在构建模型时,我们会删除一些(不必要的)相关预测变量而不包括模型,但鉴于我们正在执行 PCA,我们不会这样做,因为应用 PCA 的想法是生成新的主成分(它们不会相互关联)并用降低的维度替换当前的预测变量集。
1.
2. pcmol <- prcomp(ca_eeued, scale. = TRUE, center = TRUE)
3.
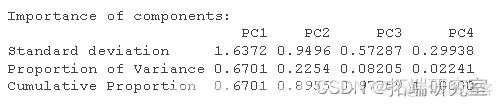
通过观察 PCA 的输出,我们可以看到前两个 PC 解释了数据中 89% 的可变性。
通过包括 3 个 PC,该模型将解释 97% 的可变性,但由于 2 个 PC 可以解释大约 90% 的数据,因此我将只使用 2 个 PC。
- 此外,通过观察下面的碎石图和每个PC的重要性,我们也可以理解,只用两个PC是可以的。
1. sumacamel = summary(adel)
2.
3. plot(pc_el,type = "l")
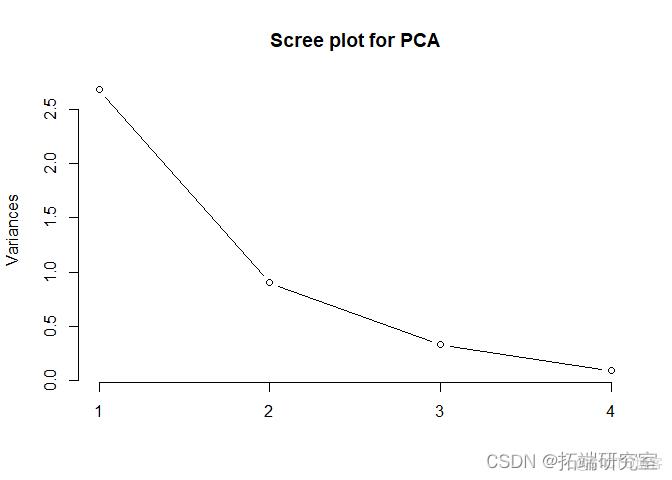
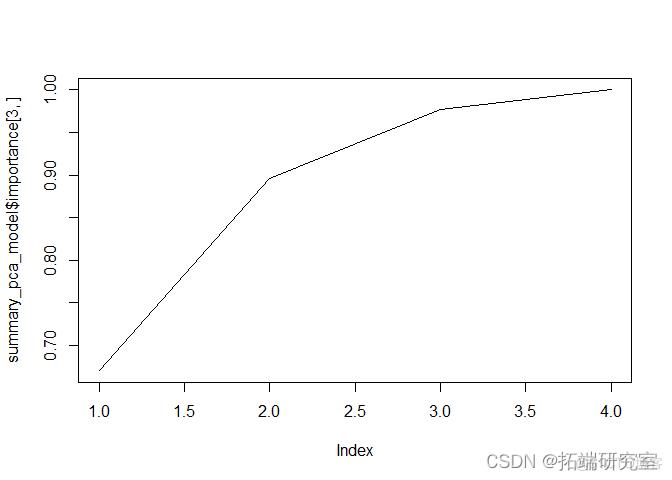
由于我们只坚持前两个主成分,现在我检查每个预测变量对每个主成分的影响量。
下面我根据它们对每个PC 的影响按降序排列了这些特性。
1. #对于PC 1
2. longScrsPC_1 <- pcael$roto[,1]
3. faccore_PC_1 <- abs(odingcre_PC_1)
4. fa_scre_PC_1raked <- nmes(rt(fac_cos1,decreasing = T))
5.
pamod$roatn[fa_coC__and,1]


现在我们最终在这两个 PC 上绘制原始数据,并检查我们是否可以分别识别每个价格组的数据点。
1.
2. #PC_n2 <- qplot(x=PC1, y=PC2
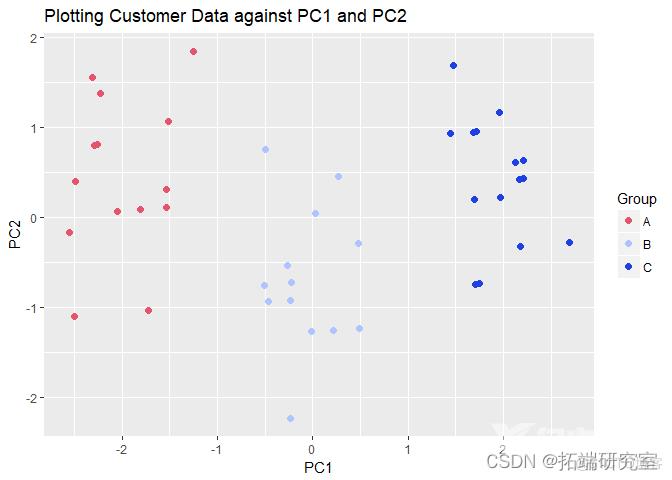
我们可以看到数据点是根据它们所在的每个价格进行聚类的!
使用上述特征,现在我们将尝试根据他/她对所考虑的特征给出的评级来预测一个人会购买哪种类型的汽车!
让我们假设一个客户对每个特征给出了以下评级:
安全:9 环境:8 创新:5 声望:4
现在让我们尝试预测该客户将属于哪个价格组:
1. new_ser <- c(9,8,5,4)
2.
3. new_cus_group <- predict(pcmdl, newdata = car_pef_ecew_c[nrow(),]
4.
5. lt_3 <- pot_2 + ge_point(aes(x=newcus_
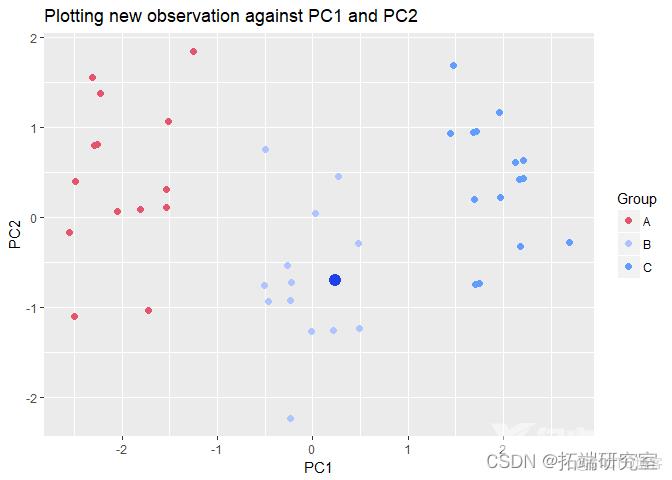
通过观察这个新观察值在 PC1 和 PC2 上的位置,我们可以得出结论,新客户更有可能购买价格组 B 的汽车!如果我需要做出一些不同的预测,我个人会使用这种方法,因为它非常快速且易于理解和解释。这种方法可以扩大规模以构建 PC 回归模型,尤其是当预测变量相关且需要正则化时。

