老友们好 !本期将对堆之构建进行解说 !
相信,初学此章节的老友 !!或多或少,对前一期的部分代码,有所困惑!
说真的,堆的有些内容理解起来还是挺困难的!
好了,废话不多讲!开始本期的解析之旅吧 !希望大家都能有所收获 !!
下面,先看一组,上一期的图示:>

那么该如何操作,才能取得前几名的数值呢?
针对这点,部分老友,可能,会用数组的覆盖原理 !
即是 将堆顶元素弹出后,再找出次大的数值。这一后续过程,想到了值的覆盖原理 !那么,究竟是否正确?弊端在哪里?
下列图示,可为老友们,解答疑惑 !
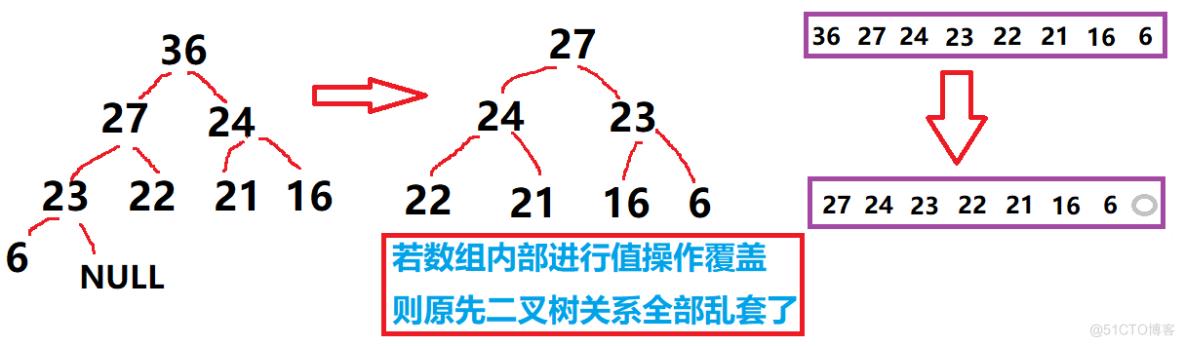
由上图可知,按照上述想到的方法,显然会出现严重的 “紊乱”现象发生!即是 父子兄弟关系,全部乱套了 !!
这样子,不仅效率低下,而且再找次大的时候,需要对剩余元素重新进行建堆 !而每一次建堆的时间复杂度是 O(N*logN)
有关于,建堆之时间复杂度,会在后续章节进行讲解 !!
而对上述问题,解决之道是,封装一个函数,进行每次查找的时候
时间复杂度是 O(N) 这意味着,只需要每一次查找,遍历一遍即可,根本无须一遍又一遍的建堆操作 !!
然而这块思想逻辑的实现,是本章节的一大难点之一 !不好理解 !
下面图示,就是上一期所写就的 向上调整算法 !!
称之为算法,在这里一点儿都不过分 !!
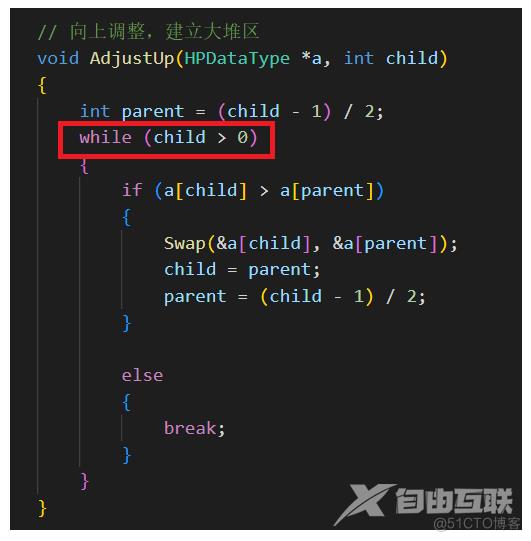
请注意,上述红色方框内的 条件判断 !!
而很多老友,不明白这种思想逻辑;
甚至对前面的二叉树遍历,并没有打牢基础,会很容易掉进坑里 !!
下面展现错误写法 :>
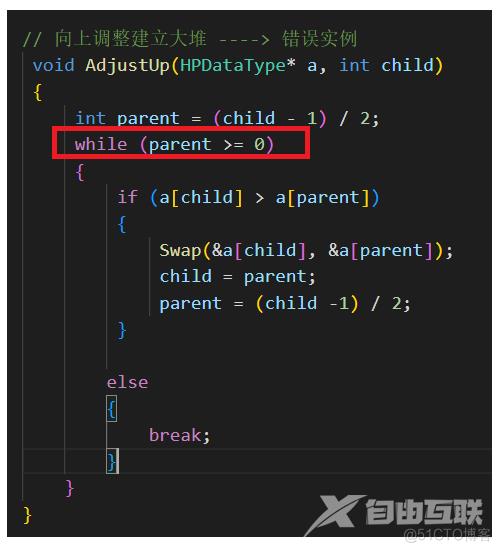
这种写法,逻辑上的漏洞是在那里?先说答案好了!
----> "parent" 与 “child” 会最终重合在一起,无法进行建大堆操作
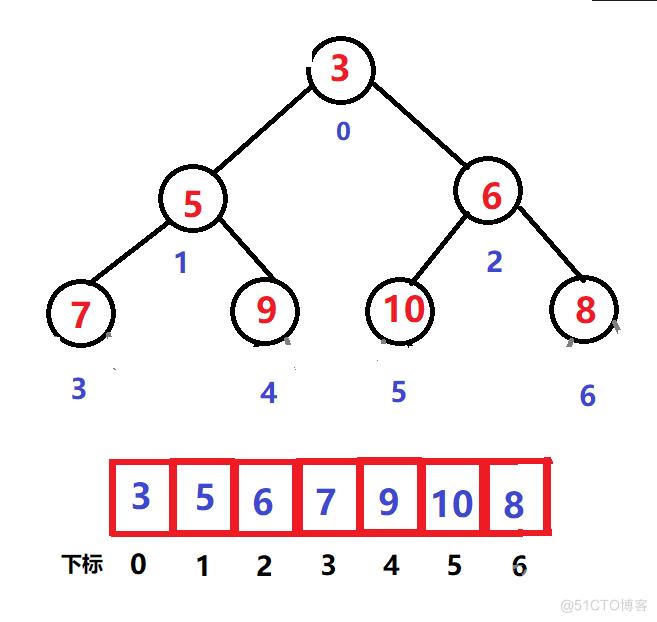
如上图所示,是小堆,然后建立大堆
若还是比较难理解,只需,将parent取特殊值检验即可
比如,令 parent = 0 ;进入循环体之后,满足条件,“孩子结点”更新为 下标是 0;此后“双亲结点”也会被更新为 下标是 0,注意取整操作,虽然 双亲结点---> parent = (0 - 1)/ 2 ---> - 1 / 2 , 取整后仍然是 0 ,此时便不符合建立大堆要求 !
现在,剖析一下,错误想法的来源,其实这才是有意思的地方 !
