齐次坐标与投影几何

这篇文章通俗易懂地解释了齐次坐标和投影几何的概念和他们在图形学中的作用.

目录

• 术语
• 并非四元数
• 二维中的投影几何
• 将其应用至三维
• 当W=1时
• 从数学上看
• 图形学中齐次坐标的应用
  • 三维坐标的平移矩阵
  • 透视(投影)变换
  • 表示平行光
• 总结

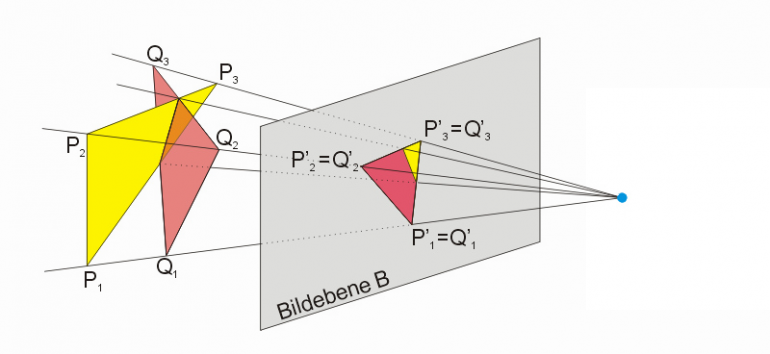
本文翻译自:Explaining Homogeneous Coordinates & Projective Geometry
这篇文章通俗易懂地解释了齐次坐标和投影几何的概念和他们在图形学中的作用.

术语

大多数时候我们使用三维坐标系,从欧式几何(Euclidean geometry)的角度来看待问题--即,三维空间中的坐标分为X,Y,Z三个维度.但是,在某些情况下从投影几何(projective geometry)的角度来思考问题是更好的.投影几何有一个额外的维度,称之为W.在此基础上的四维空间被称为"投影空间"(projective space),并且坐标在投影空间中被称为"齐次坐标"(homogeneous coordinates).

并非四元数

四元数看起来有点像齐次坐标.他们都是四维向量,并且通常都被描述为(X,Y,Z,W).然而,四元数和齐次坐标是不同的概念,有不同的作用(四元数主要用来描述旋转矩阵,这里不展开).

二维中的投影几何

首先,在谈论三维之前,我们来看一下投影几何如何在二维中起作用.
想象一个正在投影二维图像到屏幕上的投影仪.很容易定义被投影图像的X和Y维度:

现在,如果你从二维图像退后一步,看看投影仪和屏幕,你同时也可以看到W维度.W维度是从投影仪到屏幕的距离.

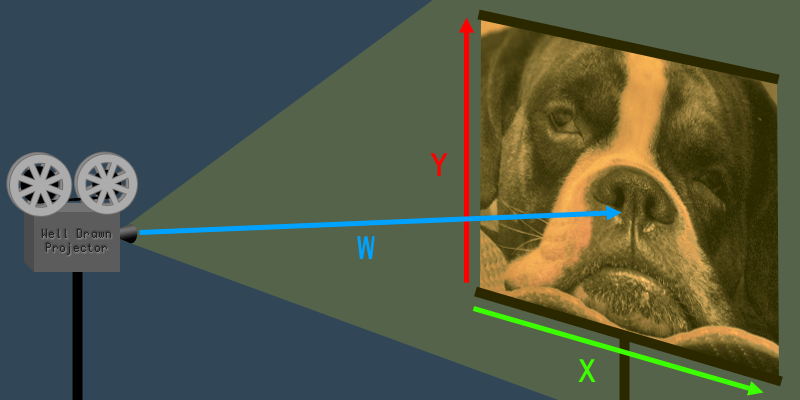
那么,W维度究竟是做什么的呢?想象一下,如果你增加或减少W,即增加或减少投影仪与屏幕之间的距离,二维图像会发生什么.如果移动投影仪靠近屏幕,整个二维图像会缩小.如果移动投影仪原理屏幕,二维图像会变大.如你所见,W的值会影响图像的大小(或者说比例).

将其应用至三维

(目前)还没有三维投影仪这种东西,因此很难想象在三维空间中的投影几何.但是,W值的作用与二维空间中的完全相同.当W增加时,坐标将扩展(放大).当W减小时,坐标将收缩(缩小).W基本上代表着三维坐标的缩放变换。

当W=1时

一般建议当将三维坐标转换为四维坐标时,应始终把W设置为1.这样做的原因是当你将坐标用1为系数来缩放时,它不会收缩或增长,只会保持相同的大小.因此,当W=1时,它对X,Y 和Z值没有影响.
因此,当涉及到三维图形学时,只有当W=1时坐标才被称为“正确”.如果使用W>1的坐标渲染,所有内容最后看起来都会被缩小.而使用W<1的坐标渲染时,所有内容最后看起来都会被放大.如果尝试使用W=0进行渲染,程序在尝试除以零时会直接崩溃.当W<0,一切都会从前到后翻转过来.
从数学上讲,不存在"不正确"的齐次坐标.使用W=1的坐标只是三维计算机图形学的一个有效的约定。

从数学上看

现在让我们来看看一些实际的数据,看看它从数学角度是如何起作用的.
假设投影仪距离屏幕3米,并且在二维图像上的坐标(15,21)处有一个点.它的投影(齐次)坐标向量(X,Y,W)=(15,21,3).

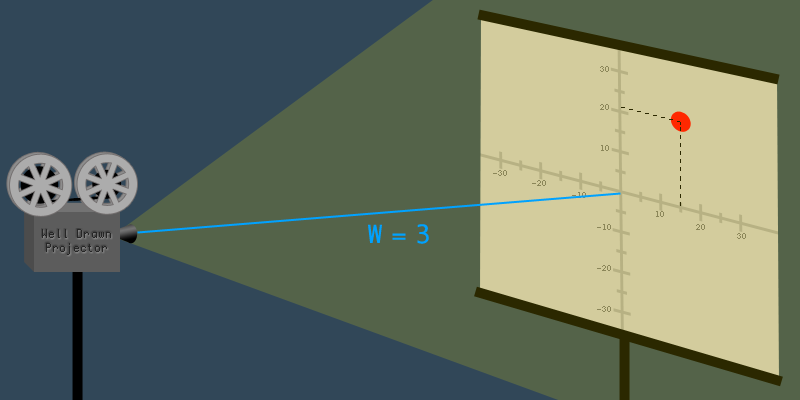
现在,想象这个投影仪被推到离屏幕1米的地方.投影仪离屏幕越近,图像就变得越小.投影仪被移近了三倍,因此图像缩小了三倍,如果我们取原始坐标向量并将所有值除以三,则得到W=1的新向量:

\[(\frac{15}{3}, \frac{21}{3}, \frac{3}{3}) = (5, 7, 1) \]

这个点现在在坐标(5,7).

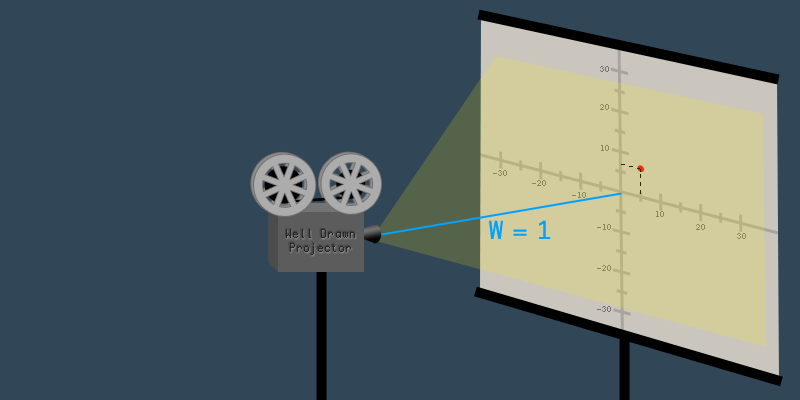
这就是一个"错误"的齐次坐标转换为"正确"的齐次坐标的过程:对所有的值除以W.这个过程对于二维和三维坐标是完全相同的.

这里是一个四维(三维齐次)坐标的例子:

\[\frac{1}{5} (10, 20, 30, 5) = (\frac{10}{5}, \frac{20}{5}, \frac{30}{5}, \frac{5}{5}) = (2,4,6,1) \]

这个例子使用C++和GLM编写是这样的:

glm::vec4 coordinate(10, 20, 30, 5);
glm::vec4 correctCoordinate = (1.0/coordinate.w) * coordinate;
//now, correctCoordinate == (2,4,6,1) 

图形学中齐次坐标的应用 三维坐标的平移矩阵

旋转和缩放变换矩阵只需要三行三列(这是由于旋转和缩放都是线性变换).但是,为了进行平移,矩阵至少需要有四列.这就是为什么图形学中的变换矩阵通常是4x4矩阵.但是,由于矩阵乘法的规则,一个有四列的矩阵不能与一个三维向量相乘.一个4x4矩阵只能与一个四维向量相乘,这就是为什么我们在三维图形学经常使用齐次坐标而不是三维空间坐标。
当在矩阵变换中使用齐次坐标时,第四维的W通常是不变的.当三维坐标转换为四维(齐次)坐标时,W被设置为1,应用变换矩阵后通常仍然为1,此时可以通过忽略W将其转换回三维坐标.对于所有平移,旋转和缩放变换都是如此.投影矩阵是个例外,它会影响W维度.

透视(投影)变换

在三维世界中,"透视"是"近大远小"的现象.如果这只猫离相机足够近,远处的山可能比猫还小.

透视是在三维图形中通过使用更改每个顶点的W元素的转换矩阵来实现的.在相机(视口)变换之后,投影变换之前,每个顶点的Z值表示与相机的距离.因此,Z值越大,顶点坐标就被缩放得越小.W维度会影响缩放,因此投影矩阵只是根据Z值更改W值.下面是应用于齐次坐标的透视投影矩阵的示例：

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 2 \\ 3 \\ 4 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \\ 4 \\ 4 \end{bmatrix} \]

注意W值根据Z值变换成了4.
应用透视投影矩阵后,每个顶点都会经历"透视除法".如前所述,"透视除法"只是将齐次坐标转换回W=1形式的特定术语.继续上面的示例,透视除法步骤将如下所示:

\[\frac{1}{4} (2, 3, 4, 4) = (0.5, 0.75, 1, 1) \]

透视分割后,W值将被丢弃,并且我们只剩下一个已根据三维透视投影正确缩放的三维坐标.

在GLM中,这个透视投影矩阵可以用函数glm::perspective或者glm::frustum来创建.在老式的OpenGL中,同时使用gluPerspective或者gluFrustum来创建.在OpenGL中,透视除法在每个顶点的顶点着色器(vertex shader)运行后自动进行.这就是顶点着色器的主要输出gl_Position为什么是一个四维向量而不是三维向量的原因.

注意,这里作者举的透视投影的例子非常简单,实际上透视投影的矩阵需要根据参数经过一定的推导才能得出,参考OpenGL Projection Matrix

表示平行光

本段的翻译略有调整,但是整体的意思应该没有差别

在齐次坐标中W=0貌似是没有意义的,如果尝试将W=0的齐次坐标转换为正确的齐次坐标(W=1),则会导致一些除零的运算:

\[\frac{1}{0} (2, 3, 4, 0) = (\frac{2}{0}, \frac{3}{0}, \frac{4}{0}, \frac{0}{0}) \]

这意味着W=0的齐次坐标不可以转换为三维坐标.

这有什么用呢?
我们可以规定W=0的齐次坐标可以看作在无穷远处的一个点,如果我们把他看作一个光源,则可以看作一个平行光(Directional Lights),并把它的X,Y,Z三个分量看作是平行光的方向.在传统的三维图形学中,平行光与点光源的区别在于光的位置向量的W值.如果 W=1,则为点光源.如果 W=0,则它是平行光.
平行光和点光源通常因为行为方式的不同,通常需要不同的代码来实现.典型的光照着色器可能如下所示:

if(lightPosition.w == 0.0){
    //directional light code here
} else {
    //point light code here
}

总结

齐次坐标具有一个用于缩放X,Y和Z维度的的额外维度W.
平移变换和透视投影变换的矩阵只能应用于齐次坐标,这就是为什么齐次坐标在三维图形学中如此普遍的原因.一般规定W=1的齐次坐标为"正确"的齐次坐标.任何齐次坐标可以通过除以W分量(透视除法)转换为"正确"的齐次坐标,除了W=0的情况.当W=0时,我们一般用其来表示一束平行光的方向