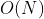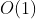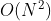联机算法和脱机算法[Alg_001]

来源：互联网收集：自由互联发布时间：2022-05-15

一、联机算法1、定义也叫在线算法，在算法执行过程中的任意时刻，只对要操作的数据进行一次扫描，扫描完成后便此后不再对已经操作过的数据进行保存和记忆。这种算法有种特

一、联机算法 1、定义

也叫在线算法，在算法执行过程中的任意时刻，只对要操作的数据进行一次扫描，扫描完成后便此后不再对已经操作过的数据进行保存和记忆。

这种算法有种特点：如果数据是储存在磁盘或者磁带上，便可以顺序地读取，无需在主存中储存数据的任何部分。

2、举例

在处理最大子序和的问题中，存在一种联机算法，具体实现如下（基于C）：

 1 int MaxSubsequenceSum(const int A[ ], int N) {
 2     int TempSum, MaxSum;
 3 
 4     TempSum = MaxSum = 0;
 5     for (int i = 0; i < N; i++) {
 6         TempSum += A[i];
 7 
 8         if (TempSum > MaxSum) {
 9             MaxSum = TempSum;
10         }
11         else if (TempSum < 0) {
12             TempSum = 0;
13         }
14     }
15 
16     return MaxSum;
17 }

可见，该算法的在执行过程中只对序列进行一次扫描，并且无需记忆已经操作过的数据，这就是联机算法，它对已经读入的数据，当即就可以给出最大子序和。

此外可以注意到，该算法的时间复杂度为 O(N) ，空间复杂度为 O(1) ，即线性时间常量空间，满足这一条件的联机算法几乎可以认为是完美的算法。

二、脱机算法 1、定义

也叫离线算法，在算法执行前所有的输入数据已知，换句话说，对于一个离线算法，在开始时就需要知道问题的所有输入数据，和需要进行的所有操作，而且在解决一个问题后就要立即输出结果。

2、举例

同样是序列最大子序和的问题，如下采用的算法便是脱机算法，具体实现（基于C）：

 1 int MaxSubsquenceSum(const int A[], int N) {
 2     int TempSum, MaxSum;
 3     
 4     MaxSum = 0;
 5     for (int i = 0; i < N; i++) {
 6         TempSum = 0;
 7         for (int j = 0; j < N; j++) {
 8             TempSum = A[j];
 9 
10             if (TempSum > MaxSum) {
11                 MaxSum = TempSum;
12             }
13         }
14     }
15 
16     return MaxSum;
17 }

可以看出，在算法执行过程中，需要不止一次地对数据进行扫描，虽然就空间复杂度而言，依然是 O(1) ，但其需要对数据进行记忆，需要把全部数据读入主存中。此外，算法的时间复杂度为 $O(N^{2})$ ，相较于上文中的联机算法就稍逊一筹。

三、理解

由于对数据的处理方式不同，联机算法在结果的产生上便形成了较为明显的区别：

对联机算法而言，中途每一次读入数据产生的结果都是满足要求的结果，其结果的产生是基于对当前及过去的所有输入，可以理解为：“热炒热卖”、“炒多少，卖多少，炒好一盘上一盘”，相当于炒菜，这也正和“在线算法”中“在线”的意义不谋而合。

而脱机算法则是利用所有的数据参与计算，最终得到一个结果，其时间复杂度是非线性的，需要对数据多次扫描，无法像联机算法一样顺序读入并出结果，可以理解为：“菜全部做好了再开始营业”，相当于自助餐厅，Ready。

上一篇：Java基础之浅谈继承、多态
下一篇：没有了

联机算法和脱机算法[Alg_001]

相关文章