论文地址:链接
代码地址:链接
论文简介:
- 此篇论文是在CGNet上增加部分限制loss而来
- 核心部分是将gt框变为mask进行蒸馏
注释:仅为阅读论文和代码,未进行试验,如有漏错请不吝指出。文章的疑惑和假设仅代表个人想法。
二. 详细 2.1 Focal Distillation 2.1.1 mask计算此篇文章在目标检测蒸馏中对FPN层进行限制,正常的操作如下公式(1)所示:
\[L_{f e a}=\frac{1}{C H W} \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W}\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2} \]此篇文章将gt的mask引入到蒸馏中:
如下公式(2),目标为1,背景为0,获得mask矩阵\(M_{i,j}\)
\[M_{i, j}= \begin{cases}1, & \text { if }(i, j) \in r \\ 0, & \text { Otherwise }\end{cases} \]但是会出现一个问题,小目标的mask区域太小,比例严重失调会导致小目标的蒸馏效果比较差,解决方法是进行归一化操作,如下公式(3)所示,引用一个尺度(缩放)量\(S_{i,j}\) , 前景尺度目标大小倒数,目标越大mask越大,但数值越小。背景为mask=0的倒数。也就是每个gt数值和为1,全部背景为1。
疑惑一: 假设前景gt为10,那么前景数值和为10,背景和为1,会不会导致比例失调?
\[\begin{gathered} S_{i, j}= \begin{cases}\frac{1}{H_{r} W_{r}}, & \text { if }(i, j) \in r \\ \frac{1}{N_{b g}}, & \text { Otherwise }\end{cases} \\ N_{b g}=\sum_{i=1}^{H} \sum_{j=1}^{W}\left(1-M_{i, j}\right) \end{gathered} \]假设一: 假设修改为前景和为1,背景和也为1。前景每个gt数值和相同。如下公式(4)所示,\(N_{gt}\) 为gt的数量
\[\begin{gathered} S_{i, j}= \begin{cases}\frac{1}{H_{r} W_{r} N_{gt}}, & \text { if }(i, j) \in r \\ \frac{1}{N_{b g}}, & \text { Otherwise }\end{cases} \\ N_{b g}=\sum_{i=1}^{H} \sum_{j=1}^{W}\left(1-M_{i, j}\right) \end{gathered} \]2.1.2 注意力特征计算这部分参考attention机制,蒸馏也要针对性的对channel和spatial进行学习
以下公式(5)是针对上面两个注意力的计算方式,注意得加绝对值!没有可解释的,就是基础操作。
\[\begin{gathered} G^{S}(F)=\frac{1}{C} \cdot \sum_{c=1}^{C}\left|F_{c}\right| \\ G^{C}(F)=\frac{1}{H W} \cdot \sum_{i=1}^{H} \sum_{j=1}^{W}\left|F_{i, j}\right| \end{gathered} \]\[\begin{gathered} A^{S}(F)=H \cdot W \cdot \operatorname{softmax}\left(G^{S}(F) / T\right) \\ A^{C}(F)=C \cdot \operatorname{softmax}\left(G^{C}(F) / T\right) \end{gathered} \]2.1.3 loss融合直接看下面的公式(7),前景和背景分开进行监督,公式比较简单,\(M_{i,j}\)表示mask,\(S_{i,j}\) 表示mask的尺度,\(A_{i,j}^S/A_k^C\) 表示teacher的注意力特征。
\[\begin{aligned} &L_{f e a}=\alpha \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W} M_{i, j} S_{i, j} A_{i, j}^{S} A_{k}^{C}\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2} +\beta \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W}\left(1-M_{i, j}\right) S_{i, j} A_{i, j}^{S} A_{k}^{C}\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2} \end{aligned} \]疑惑二: 将上面的公式合并,明显看出 \(\alpha/\beta\) 就表示前景和背景的比例,这明显印证了疑惑一的问题。再从论文图表(7)中调参发现,这两个参数对实际的精度影响不大 \(\pm0.3\) 的精度差异,是否可直接使用假设一的方案,直接去除此两个参数。
由于公式(7)仅对teacher的注意力特征进行了使用,并未对student的注意力特征进行监督,所以引出下面的公式(8)直接监督
\[L_{a t}=\gamma \cdot\left(l\left(A_{t}^{S}, A_{S}^{S}\right)+l\left(A_{t}^{C}, A_{S}^{C}\right)\right) \]疑惑三: 为什么公式(7)需要使用teature注意力特征而不使用student的注意力特征?论文没有给出答案,issue上作者也没有给出答案。
假设三:
- 公式(7)中直接去除 \(A_{i,j}^S/A_k^C\) 是否合适?
- 将公式(8)合并到公式(7)中,比如下式的公式(9)所示,当然可以有其他形式
此部分来自于CGNet,不做过多介绍,理解较为容易
三. 题外话 3.1 一些可能的笔误此论文的开源项目基于mmdetection实现,其中试验的YOLOX蒸馏试验有点瑕疵:
- 第一个问题
以下是此论文的项目readme,YOLOX-m的baseline是45.9,但实际YOLOX官方精度是46.9,差一个点已经是非常大了。
作者说用mmdet跑出来YOLOX-m就是这个精度,本人比较怀疑,因为之前跑的YOLOX-S/nano都没问题,YOLOX-m正在试验下周一出结果。
结果: 确实像作者说的达不到官方的精度,本人替换focus到conv,其它未改变,mAP45.2比作者的还低0.7
- 第二个问题
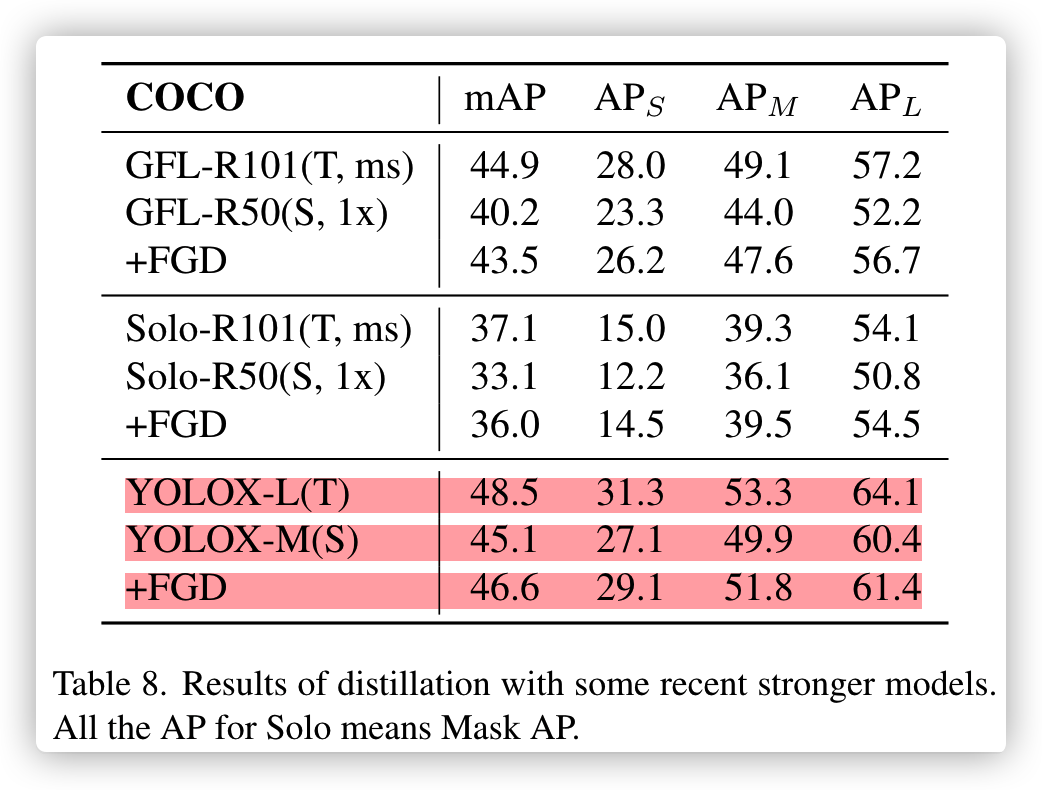
论文中YOLOX-m和repo中的精度不一致,论文45.1,repo是45.9,论文是笔误?
YOLOX-L的精度mmdet已经试验为49.4,为啥这里是48.5?这也是笔误?
 3.2 论文观后感
3.2 论文观后感
之前见过类似的做法,用作弱监督中。但未看到将mask用作蒸馏之内,这让我开眼界了。
刚开始看论文的效果确实不错,因为本人对YOLOX较为熟悉,所以仔细看了一下这部分,发现上述问题,作者也没重视。。。
以后实际项目尝试一下,这次仅仅作为阅读论文
