低温与高密度的条件:
\[kT\ll \varepsilon _F,T\ll T_F \](能量远小于费米能量,温度远小于费米温度)。
应用Sommerfield方法
自由费米气体是费米系统,应用费米系统的巨配分函数,所计算某个物理量的期望的表示为:
\[I=\int_0^{\infty}{d\varepsilon \frac{f\left( \varepsilon \right)}{e^{\beta \left( \varepsilon -\mu \right)}+1}} \]其中,$ n\left( \varepsilon \right) =\frac{1}{e^{\beta \left( \varepsilon -\mu \right)} +1} $.
画出其函数图像:
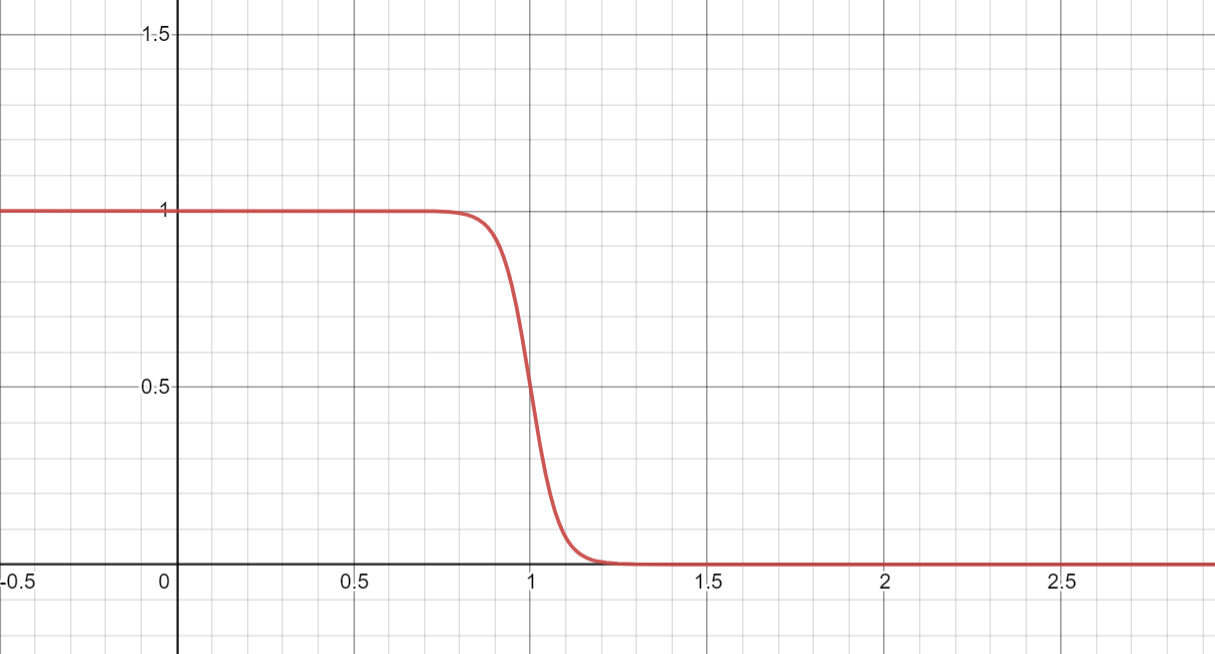
设 \(F(\varepsilon)\) 为 \(f(\varepsilon)\) 的原函数,
\[F\left( \varepsilon \right) =\int_0^{\varepsilon}{d\varepsilon \,\,f\left( \varepsilon \right)} \]则,积分 \(I\) 变为(应用一次分部积分):
\[I=\int_0^{\infty}{d\varepsilon \frac{dF\left( \varepsilon \right)}{d\varepsilon}n\left( \varepsilon \right)}=-\int_0^{\infty}{d\varepsilon F\left( \varepsilon \right) \frac{dn\left( \varepsilon \right)}{d\varepsilon}} \]计算 \(n(\varepsilon)\) 的导数:
\[\frac{dn\left( \varepsilon \right)}{d\varepsilon}=-\frac{\beta e^{\beta \left( \varepsilon -\mu \right)}}{\left( e^{\beta \left( \varepsilon -\mu \right)}+1 \right) ^2} \]带入积分式得:
\[I=\int_0^{\infty}{d\varepsilon F\left( \varepsilon \right) \frac{\beta e^{\beta \left( \varepsilon -\mu \right)}}{\left( e^{\beta \left( \varepsilon -\mu \right)}+1 \right) ^2}} \]做一个变量代换:\( \xi =\beta \left( \varepsilon -\mu \right) \),\( d\xi =\beta d\varepsilon \),得到:
\[I=\int_{-\beta \mu}^{\infty}{d\xi F\left( \mu +kT\xi \right) \frac{e^{\xi}}{\left( e^{\xi}+1 \right) ^2}}\doteq \int_{-\infty}^{\infty}{d\xi F\left( \mu +kT\xi \right) \frac{e^{\xi}}{\left( e^{\xi}+1 \right) ^2}} \](这里是因为\(T\rightarrow 0\), 所以 \(\mu=\frac{1}{kT}\rightarrow \infty\)).
对 \(F(\mu+kT\xi)\) 作 \(\mu\) 附近的泰勒展开,
代入积分式得到(奇数项全部为0,只剩下偶数项,然后 \(\int_{-\infty}^{\infty}g(x)dx=2\cdot\int_{0}^{\infty}g(x)dx\),\(g(x)\) 为偶函数):
\[I\doteq 2\sum_{n=0}^{\infty}{F^{\left( 2n \right)}\left( \mu \right) \left( kT \right) ^{2n}\frac{1}{\left( 2n \right) !}\int_0^{\infty}{d\xi \frac{\xi ^{2n}e^{\xi}}{\left( e^{\xi}+1 \right) ^2}}} \]令其中的
\[c_n=\frac{1}{\left( 2n \right) !}\int_0^{\infty}{d\xi \frac{\xi ^{2n}e^{\xi}}{\left( e^{\xi}+1 \right) ^2}} \]考虑\(
\frac{e^{\xi}}{\left( e^{\xi}+1 \right) ^2}=e^{-\xi}\left( 1+e^{-\xi} \right) ^{-2}
\).
对 \(\left( 1+e^{-\xi} \right) ^{-2}\) 作泰勒展开,得到:
因而:
\[e^{-\xi}\left( 1+e^{-\xi} \right) ^{-2}=\sum_{l=1}^{\infty}{\left( -1 \right) ^{l-1}le^{-l\xi}} \]\(c_n\) 的形式为(最后一步用了 \(2n\) 次分部积分)
\[c_n=\frac{1}{2n!}\sum_{l=1}^{\infty}{\left( -1 \right) ^{l-1}l\int_0^{\infty}{d\xi \,\,\xi ^{2n}e^{-l\xi}}}=\sum_{l=1}^{\infty}{\frac{\left( -1 \right) ^{l-1}}{l^{2n}}} \]下面我们来计算前几项
计算 \(c_1\),
这里将会用到一个tricky的方法,就是 \(N^+\rightarrow\{x|\mathrm{x=even}\}\) 是一一对应的,可以由 \(f(x)=2x\) 这个映射构造。所以:
\[\sum_{l=even}{\frac{1}{l^2}}=\sum_l{\frac{1}{\left( 2l \right) ^2}} \]代入上式,得到:
\[c_1=\left( 1-\frac{2}{2^2} \right) \sum_l{\frac{1}{l^2}}=\frac{1}{2}\cdot \frac{\pi}{6}=\frac{\pi}{12} \]最后一步的求和是Riemann-Zeta函数:\(\zeta(x)\),取 \(x=2\),
\[\zeta(2)=\frac{\pi}{6} \]计算 \(c_2\),
\[c_2=\sum_{l=1}^{\infty}{\frac{\left( -1 \right) ^{l-1}}{l^4}}=\sum_l{\frac{1}{l^4}}-2\sum_{l=even}{\frac{1}{l^4}}=\left( 1-\frac{2}{2^4} \right) \sum_l{\frac{1}{l^4}}=\frac{7}{8}\zeta \left( 4 \right) =\frac{7}{8}\cdot \frac{\pi ^4}{90}=\frac{7\pi ^4}{720} \]二. 自由费米气体(高温或低密度)费米气体的状态方程用巨配分函数来表示出来:
\[\frac{PV}{kT}=\ln\mathrm{Q}=\sum_{\alpha}{\ln \left( 1+ze^{-\beta \varepsilon _{\alpha}} \right)} \]其中 \(z=e^{\beta\mu}\) 为易逸度,可以设 \(x=\beta\varepsilon\)
求和可以用态密度的方式表示为积分:
我再这里就直接写出非相对论粒子的态密度表达式:
\[D\left( \varepsilon \right) =\frac{\omega m^{\frac{3}{2}}\varepsilon ^{\frac{1}{2}}}{\sqrt{2}\pi ^2\hbar ^3} \]代入积分式得到:
\[\frac{P}{kT}=\frac{\omega m^{\frac{3}{2}}}{\sqrt{2}\pi ^2\hbar ^3}\int_0^{\infty}{d\varepsilon \,\,\varepsilon ^{\frac{1}{2}}\ln \left( 1+ze^{-\beta \varepsilon} \right)} \]做一个常数的简化,
\[\frac{\omega m^{\frac{3}{2}}}{\sqrt{2}\pi ^2\hbar ^3}\int_0^{\infty}{d\varepsilon \,\,\varepsilon ^{\frac{1}{2}}\ln \left( 1+ze^{-\beta \varepsilon} \right)}=\frac{\omega m^{\frac{3}{2}}}{2\sqrt{2}\pi ^{\frac{3}{2}}\hbar ^3}\cdot \frac{2}{\sqrt{\pi}}\int_0^{\infty}{d\varepsilon \,\,\varepsilon ^{\frac{1}{2}}\ln \left( 1+ze^{-\beta \varepsilon} \right)} \]\[\int_0^{\infty}{d\varepsilon \,\,\varepsilon ^{\frac{1}{2}}\ln \left( 1+ze^{-\beta \varepsilon} \right)}=\frac{1}{\beta ^{\frac{3}{2}}}\int_0^{\infty}{d\left( \beta \varepsilon \right) \,\,\left( \beta \varepsilon \right) ^{\frac{1}{2}}\ln \left( 1+ze^{-\beta \varepsilon} \right)}=\left( kT \right) ^{\frac{3}{2}}\int_0^{\infty}{dx\,\,x^{\frac{1}{2}}\ln \left( 1+ze^{-x} \right)} \]令 $\lambda =\sqrt{\frac{2\pi}{mkT}}\hbar $,这一整个积分式就变成了:
\[\frac{P}{kT}=\frac{\omega}{\lambda ^3}f\left( z \right) \]其中:
\[f\left( z \right) =\frac{2}{\sqrt{\pi}}\int_0^{\infty}{dx\,\,x^{\frac{1}{2}}\ln \left( 1+ze^{-x} \right)} \]现在到了正题,数学处理部分:
考虑这样一个式子(\(\frac{1}{1-a}=\sum{a^
i}\), 这个式子里,等比数列的公比无须是小量):
将它对 \(x\) 积分:
\[\ln \left( 1+ze^{-x} \right) =-\int{dx\,\,\frac{ze^{-x}}{1+ze^{-x}}}=\sum_{l=1}^{\infty}{\frac{\left( -1 \right) ^{l-1}}{l}z^le^{-lx}} \]将这个展开式代入我们要求的积分式:
\[f\left( z \right) =\frac{2}{\sqrt{\pi}}\sum_{l=1}^{\infty}{\left[ \frac{\left( -1 \right) ^{l-1}}{l}z^l\int_0^{\infty}{dx\,\,x^{\frac{1}{2}}e^{-lx}} \right]} \]现在我们要求出 \(\int_0^{\infty}{dx\,\,x^{\frac{1}{2}}e^{-lx}}\).
这是一个 \(\Gamma\)函数,还是先做变量代换把它变成标准的 \(\Gamma\)函数积分的形式:
得到:
\[\frac{1}{l^{\frac{3}{2}}}\int_0^{\infty}{d\left( lx \right) \,\,\left( lx \right) ^{\frac{1}{2}}e^{-lx}}=\frac{\sqrt{\pi}}{2}l^{-\frac{3}{2}} \]所以:
\[\frac{P}{kT}=\frac{\omega}{\lambda ^3}\sum_{l=1}^{\infty}{\left( -1 \right) ^{l-1}\frac{z^l}{l^{5/2}}} \]附录
如何求解 \(\Gamma(\frac{3}{2})\)?
而 \(\Gamma\)函数具有这样的性质:
\[\Gamma \left( \frac{3}{2} \right) =\left( \frac{3}{2}-1 \right) \cdot \Gamma \left( \frac{1}{2} \right) \]所以,要求出 \(\Gamma(\frac{1}{2})\)
\[\Gamma \left( \frac{1}{2} \right) =\int_0^{\infty}{dx\,\,x^{-\frac{1}{2}}e^{-x}} \]变量代换:
\[\Gamma \left( \frac{1}{2} \right) =\int_0^{\infty}{d\left( x^{\frac{1}{2}} \right) 2e^{-\left( x^{\frac{1}{2}} \right) ^2}=2\int_0^{\infty}{dx\,\,e^{-x^2}}} \]将其平方,然后直角坐标系变换为极坐标系:
\[\left( \int_{-\infty}^{\infty}{dx\,\,e^{-x^2}} \right) ^2=\int_0^{2\pi}{d\theta \int_0^{\infty}{dr\,\,re^{-r^2}}}=\pi \]所以
\[\int_0^{\infty}{dx\,\,e^{-x^2}}=\frac{1}{2}\int_{-\infty}^{\infty}{dx\,\,e^{-x^2}}=\frac{\sqrt{\pi}}{2} \]\[\Gamma \left( \frac{1}{2} \right) =\sqrt{\pi} \]所以
\[\Gamma \left( \frac{3}{2} \right) =\frac{\sqrt{\pi}}{2} \]