数据结构上老师已经专门讲过二叉树了,这里做一下小结,以及根据前(后),中序列求后(前)中序列的算法;
当然,二叉树概念就不引入了,这里再次提炼一下二叉树的性质:
1、满足本身是有序树。
2、树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2。
3、二叉树具有以下几个性质:
a:二叉树中,第 i 层最多有 2的i-1次方个结点。
b:如果二叉树的深度为 K,那么此二叉树最多有 2的k次方-1 个结点。
c:二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
这里也有完美二叉树:
1.满二叉树中第 i 层的节点数为 2的i-1 次方个。
2.深度为 k 的满二叉树必有 2k次方-1 个节点 ,叶子数为 2的k-1次方。
3.满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
4.具有 n 个节点的满二叉树的深度为 log2(n+1)。
对于一颗完全二叉树来讲,则一般满足一下性质:
(1)i>1的节点,其父节点为i/2;
(2)如果2i>k,那i没有孩子,如果2i+1>k,则没有右孩子
(3)节点i有孩子,那左孩是2i,右孩是2i+1;
对于二叉树的储存,我们一般用指针来实现,通过定义键值,左孩,右孩来实现二叉树的储存;
如:
struct node { int value; node *L; node *R; node(int value=0,node *L=NULL,node *R=NULL):value(value),L(L),R(R){} };
同时,节点的申请也遵循new动态内存分配和用完后delete释放内存空间;
对于二叉树的遍历,我们同样遵循图论的bfs与dfs,因为从本质上来说,二叉树就是特殊的图;
首先bfs:
在二叉树中就做层序遍历,即一层一层的进行访问;
如下图
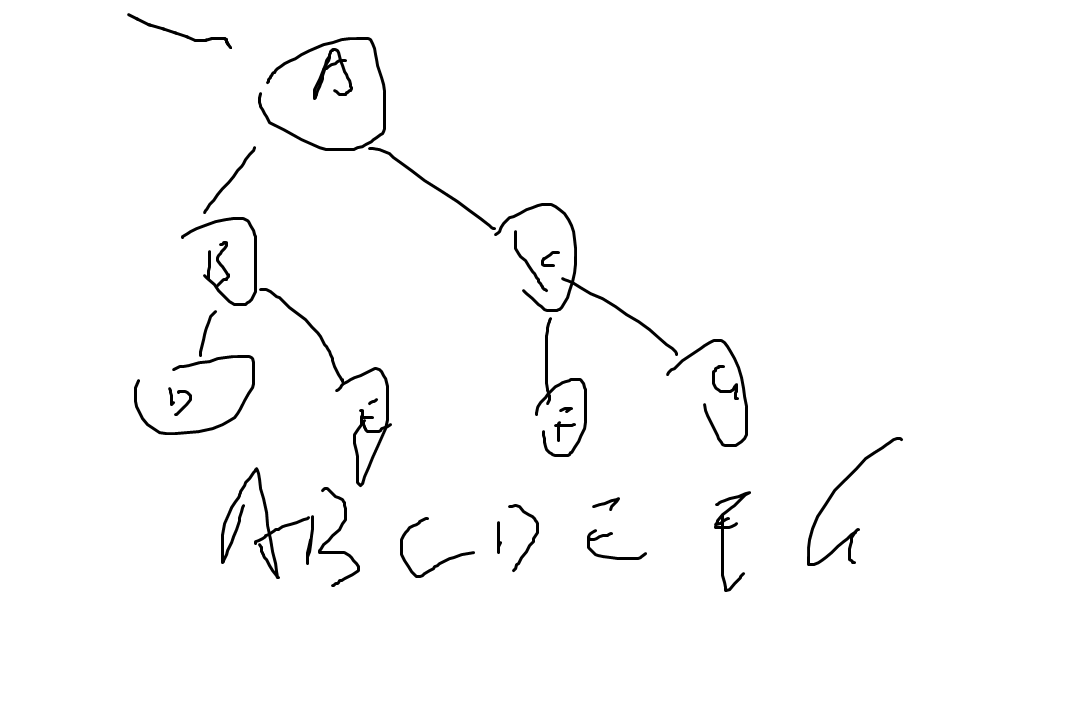
关于dfs:
用dfs实现二叉树的遍历,其实是代码很简洁而又实用的;
通常对于二叉树来讲,dfs算法遍历可以有三种实现方式,有前序遍历(即先访问头节点,在访问左子树,在访问右子树)
中序遍历(先访问左子树,在访问头节点,在访问右子树)和后序遍历(先访问左子树,在访问右子树,在访问头节点)

需要注意的是,根据前中或者后中序遍历可以确定一颗二叉树,但如果只根据前后序遍历则不能确定一颗二叉树;
-------------------------二叉树实战演练,根据前中序确定后序序列;
我们给出一组数据:
节点n:9;
前序序列:1 2 4 7 3 5 8 9 6
中序序列:4 7 2 1 8 5 9 3 6;
问:如何根据这两组序列确定后序序列?
首先我们要明白,先序遍历的第一个数是整棵树的根节点,如“1”,这就可以在中序序列中确定这颗树的左子树是“4 7 2”,右子树是“8 5 9 3 6”
然后开始递归,得到的左子树”4 7 2 “对照先序序列的第二个数“2”,则2是左子树的根,同样第三个数....第n个数
过程可以理解为下图:
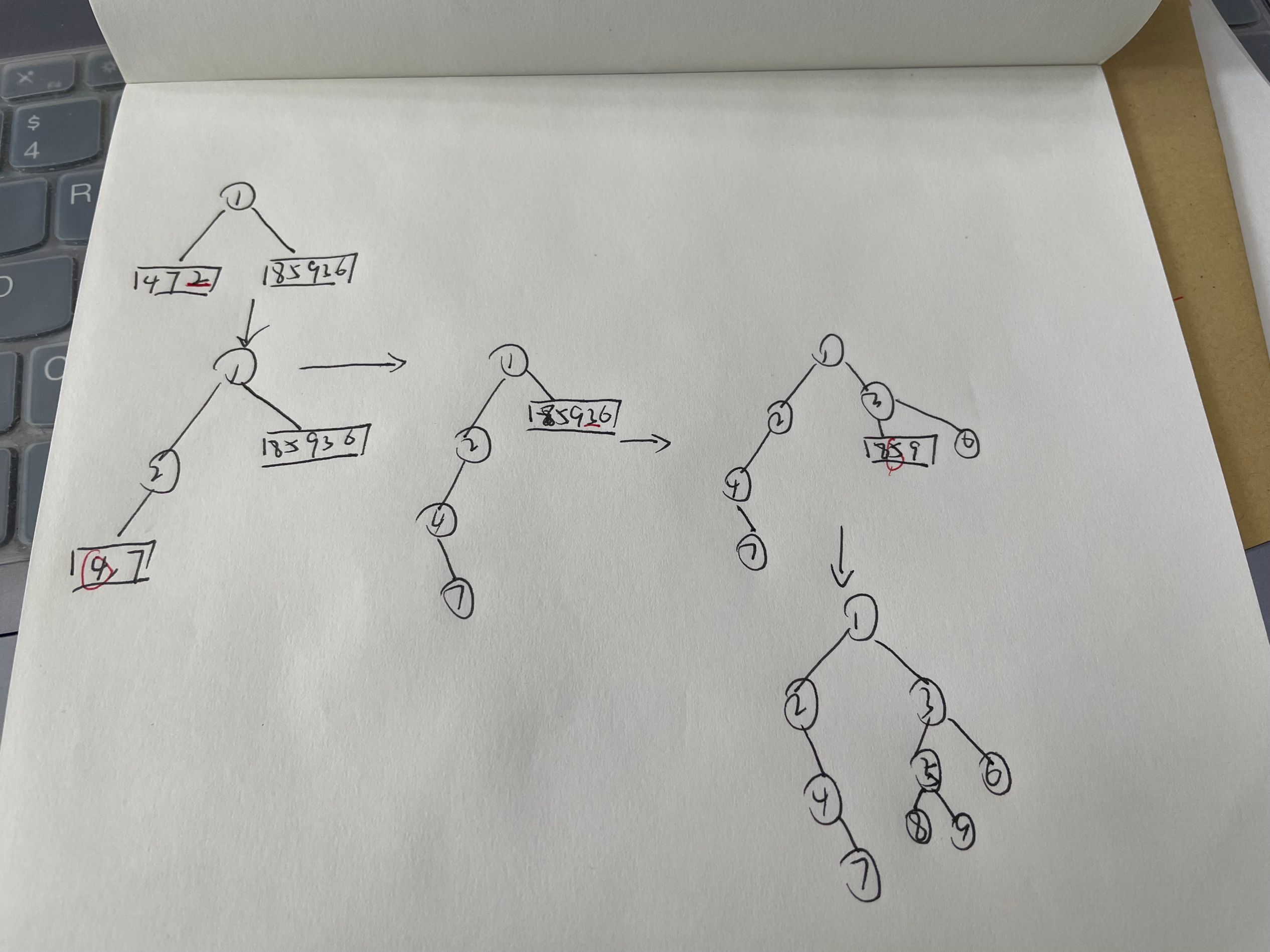
并且需要注意的是中序开头元素一定是左子树最下面的一颗左子树,中序最右边的元素一定是最下面一颗右子树
然后我们用代码进行实现一下,再次借用名言
Talk is cheap. Show me the code.1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1010; 4 int k;//统计个数 5 int n; 6 int pre[N];//前序序列 7 int in[N];//中序序列 8 int post[N];//后序序列 9 struct node 10 { 11 int value; 12 node *L; 13 node *R; 14 node(int value=0,node *L=NULL,node *R=NULL):value(value),L(L),R(R){}//初始化 15 }; 16 void buildtree(int L,int R,int &t,node * &root)//建树,左子树,右子树,前序序列值的推进,根节点 17 { 18 int flag=-1; 19 for(register int i=L;i<=R;i++) 20 { 21 if(in[i]==pre[t])//找到了线序序列的位置 22 { 23 flag=i;//对应中序序列的位置 24 break; 25 } 26 } 27 if(flag==-1)//没有就返回 28 return ; 29 root=new node(in[flag]);//新建子根节点 30 t++;//推进 31 if(flag>L)//如果是在左子树上,那中序序列遍历的根节点左边在左子树上 32 { 33 buildtree(L,flag-1,t,root->L); 34 } 35 if(flag<R)//如果是在右子树上,那中序序列遍历的根据二点右边在柚子树上,右子树需从i+1进行计数 36 { 37 buildtree(flag+1,R,t,root->R); 38 } 39 } 40 void preorder(node *root)//前序遍历 41 { 42 if(root!=NULL) 43 { 44 post[k++]=root->value; 45 preorder(root->L); 46 preorder(root->R); 47 } 48 } 49 void inorder(node *root)//中序遍历 50 { 51 if(root!=NULL) 52 { 53 inorder(root->L); 54 post[k++]=root->value; 55 inorder(root->R); 56 } 57 } 58 void postorder(node *root)//后序遍历 59 { 60 if(root!=NULL) 61 { 62 postorder(root->L); 63 postorder(root->R); 64 post[k++]=root->value; 65 } 66 } 67 void remove_tree(node *root)//删除节点释放空间 68 { 69 if(root==NULL) 70 return ; 71 remove_tree(root->L); 72 remove_tree(root->R); 73 delete root; 74 } 75 int main() 76 { 77 std::ios::sync_with_stdio(false); 78 cin>>n; 79 for(register int i=1;i<=n;i++) 80 cin>>pre[i]; 81 for(register int i=1;i<=n;i++) 82 cin>>in[i]; 83 int t=1;//同步前序序列,确定根节点 84 node *root; 85 buildtree(1,n,t,root);//建树 86 postorder(root);//后序遍历 87 for(register int i=0;i<k;i++) 88 { 89 printf("%d%c",post[i],i==k-1?'\n':' ');//输出 90 } 91 remove_tree(root);//释放空间 92 return 0; 93 }
对于代码的一些解释:
if(flag>L)//如果是在左子树上,那中序序列遍历的根节点左边在左子树上 { buildtree(L,flag-1,t,root->L); } if(flag<R)//如果是在右子树上,那中序序列遍历的根据二点右边在柚子树上,右子树需从i+1进行计数 { buildtree(flag+1,R,t,root->R); }
我们在找到根节点以后,将其放到flag里面,那么相对来讲,左子树的范围就是{L,flag-1},右子树的范围就是{flag+1,R},L,R这里指的是左右子树的边界
那这样,我们就可以确定这颗树的后序序列是1 4 2 8 9 5 6 3 1
注意一点,用完要收拾桌子,所以说在一些时候不要忘记对内存空间进行释放;
------------分割线,下面来简单说一下bst算法
bst算法原名是二叉搜索树,又叫做二叉查找树等等;
这种树这样一个特点:
对于任意节点的键值来讲,比他的所有左子树的节点键值都要大,也小于所有右子树的节点键值都要小,也就是说,以任意节点为根节点的二叉树的子树仍然是一颗bst树;
通过推论也可以知道:键值最大的节点没有右儿子,键值最小的节点没有左儿子;
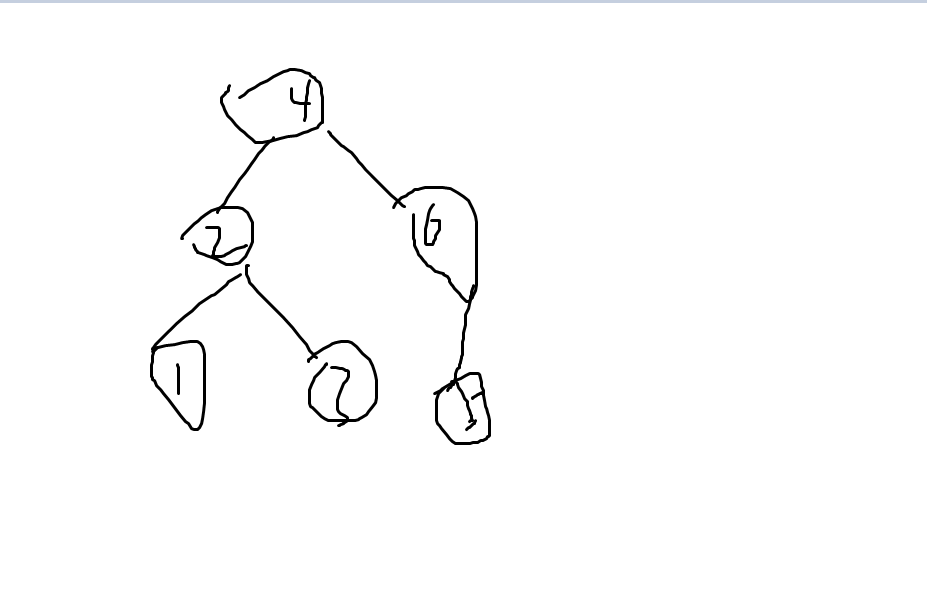
同时,通过中序序列我们可以得到bst树的有序序列
对于bst的基本操作:也无外乎于查删插
插入:
(1)建树和插入。以第1个数据为根结点,逐个插入其他所有数据。插入过程从根结点开始,如果数据γ比根结点x小,就往左x子树上插,否则就往右子树上插,如果子树为空,
直接放到这个空位.如果韭空就与子树的值进行比较再进入子树的下一层,直到找到一个空位置。新插入的数据肯定位于一个最底层的叶子结点而不是插到中间某个结点上替代原来的数据。
从建树的过程可知,如果按给定序列的顺序进行插入,最后建成的BST是唯一的。形成的BST可能很好,也可能很坏。在最坏的情况下,例如一列有序整数{1,2,3,4,5,6, 7},按顺序插入,会全部插到右子树上; BST退化成一个只包含右子树的链表,从根结点到最底层的叶子,深度是n,导致访问一个结点的复杂度是O(n)。在最好的情况下,例如序列 {4, 2,1, 3, 6, 5,7},得到的BST左、右子树是完全平衡的,深度是log2n,访问复杂度是O(log2n)。退化的BST和平衡BST如图:
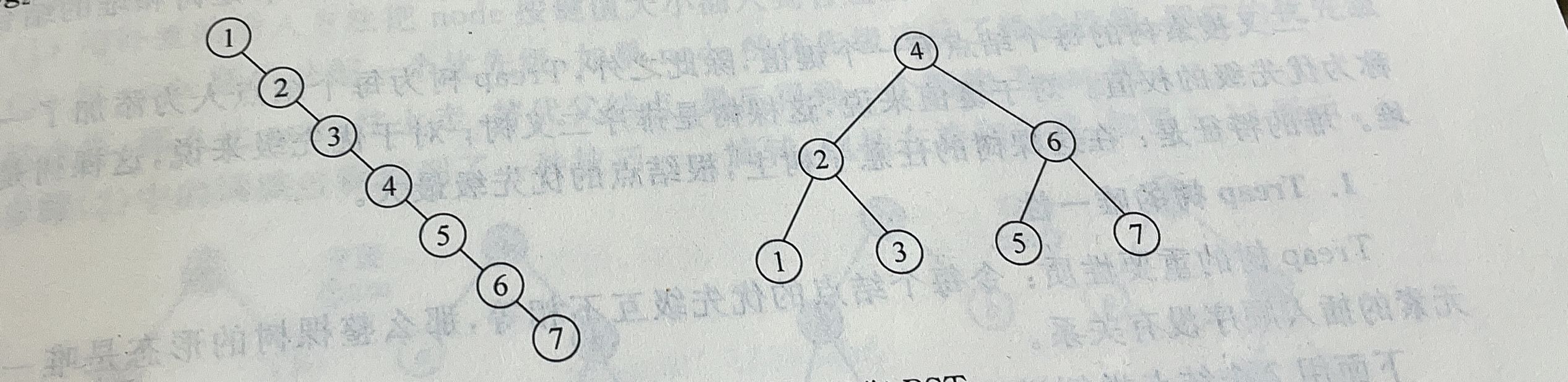
查询:从根节点递归查询即可,类似于并查集的查询;
删除:
删除分为三种情况
(1)最底层的叶节点,直接删除
(2)只有左子树或者右子树,则,删除原节点,由左子树或者右子树取而代之;
(3)最麻烦的情况,既有左子树,也有右子树
这种删除方式则需要以x为根节点的子树重构,并且遵循保持bst树的有序性的原则;
一般是用右子树的最大元素或者左子树的最小元素取代,无论如何,被选的节点最多只有一个孩子;
删除过程如下:
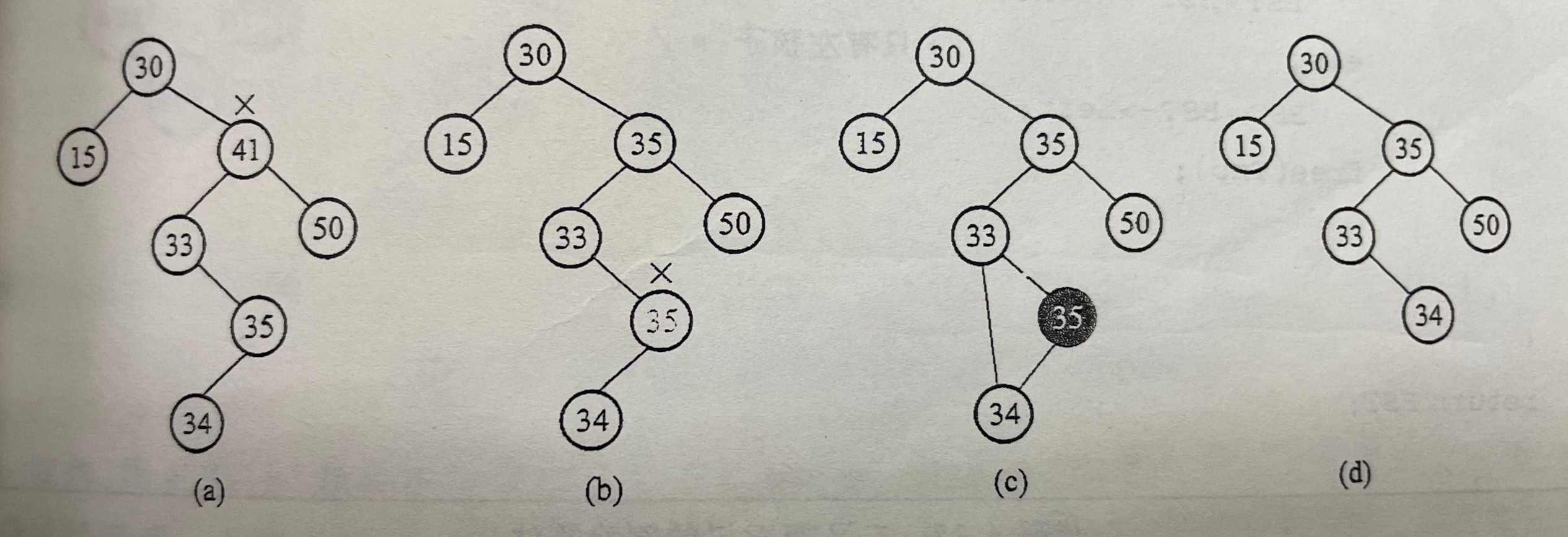
bst算法应用一般用AVL(平衡树),红黑树,树堆,sbt,splay等,算法较为广并且多用于查找
