- 1-范数: \(||X||_1=|x_1|+|x_2|+...+|x_n|\)
- 2-范数: \(||X||_2=(|x_1|^2+|x|^2+...+|x_n|^2)^\frac 12\), 其实2-范数就是通常意义下的距离
我们所说的正则化,就是在原来的loss function的基础上,加上了一些正则化项或者称为模型复杂度惩罚项。现在我们还是以最熟悉的线性回归为例子。
- 优化目标:
- 加上 L1 正则项
- 加上 L2 正则项
我们的目标是使损失越小越好。
那加了 L1 正则化和 L2 正则化之后,对目标函数的求解有什么作用呢?
3. L1 和 L2 正则化作用 假设 \(X\) 为一个二维样本,那么要求解的参数 \(w\) 也是二维:
- 原函数曲线等高线(同颜色曲线上,每一组 \(w_1,w_2\)带入值都相同)
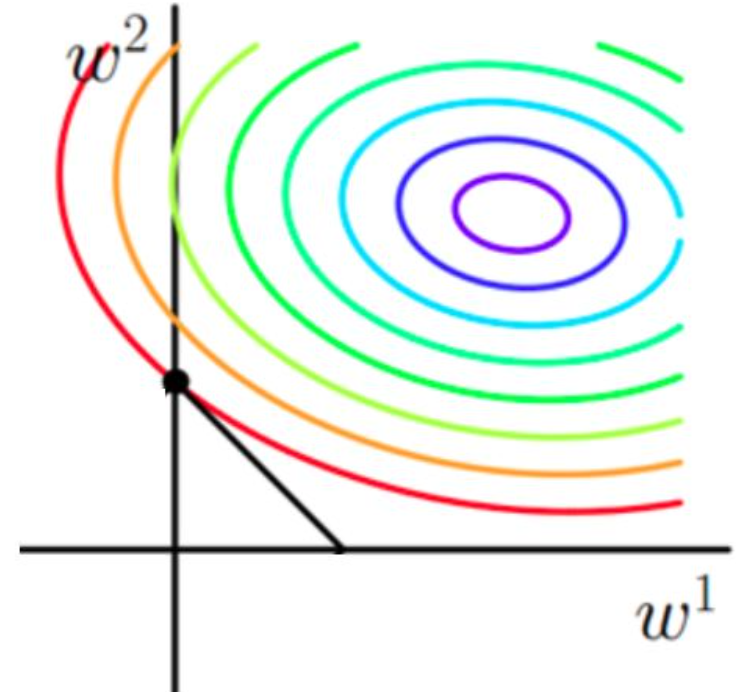
图1 目标函数等高线
- 加入 L1 和 L2 正则化的函数图像
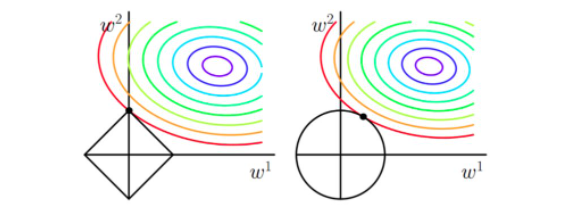
图2 加入 L1 和 L2 正则的等高线
从上边两幅图中我们可以看出:
- 如果不加L1和L2正则化的时候,对于线性回归这种目标函数凸函数的话,我们最终的结果就是最里边的紫色的小圈圈等高线上的点。
- 当加入L1正则化的时候,我们先画出 \(|w_1|+|w_2|=F\) 的图像,也就是一个菱形,这些曲线上的点算出来的 1 范数 \(|w_1|+|w_2|\) 都为 \(F\) 。那现在的目标不仅是原曲线算的值要小,即越来越接近中心的紫色圆圈,还要是的这个菱形越来越小(F 越来越小)。那么还和原来一样的话,过中心紫色圈圈的那个菱形明显很大,因此我们要取到一个恰好的值。那么如何求值呢?
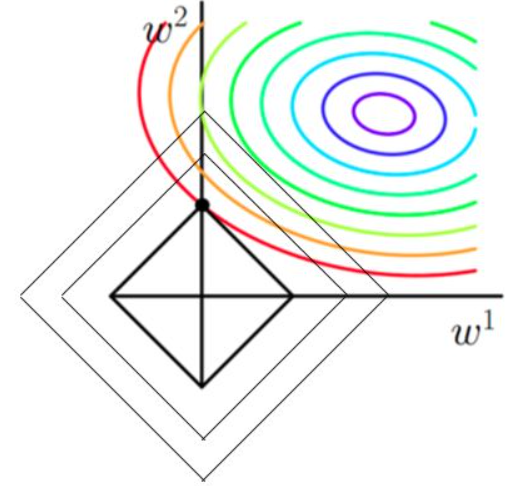
图3 带 L1 正则化的目标函数求解 3.1 为什么说菱形和等高线相切的时候损失最小?
以原目标函数的曲线来说,在同一条等高线上,以最外圈的红色等高线为例。我们可以看到,对于红色曲线上的每个点都可以做一个菱形,根据上图3可知,当这个菱形与某条等高线相切的时候,这个菱形最小。
证明:同一等高线上的点能够使得 \(\frac 1N\sum_{i=1}^N(y_i-w^Tx_i)^2\) 值相同,但是在相切的时候 \(C||w||\) 小,即 \(|w_1|+|w_2|\) 小,所以能够使得 \(\frac 1N\sum_{i=1}^N(y_i-w^Tx_i)+C||w||_1\) 更小。
那么加入 L1 范数得到的解,一定是某个菱形和某条原函数等高线的切点。
3.2 为什么加入 L1 正则化的解更容易稀疏? 我们可以观察到,几乎对于很多原函数等高线,和某个菱形相交的时候容易相交在坐标轴上,即最终结果解的某个维度及其容易为0,比如上图最终解释 \(w=(0,x)\) , 这也就是我们所说的 L1 更容易得到稀疏解(解向量中 0 比较多)的原因。
证明:假设只有一个参数为\(w\),损失函数为\(L ( w )\),分别加上 \(L1\) 正则项和 $L2 $正则项后有:
\[J_{L1}(w)=L(w)+\lambda|w| \\ J_{L2}(w)=L(w)+\lambda|w|^2 \]假设\(L ( w )\) 在 0 处的导数为\(d_0\) ,即
\[ \frac{\partial L(w)}{\partial w} \bigg |_{w=0} =d_0 \]则可以推导使用L1正则和L2正则时的导数。
引入L2正则项,在0处的导数
\[\frac{\partial J_{L2}(w)}{\partial w} \bigg |_{w=0} =d_0 + 2 \times \lambda \times w = d_0 \]引入 L1 正则项,在0处的导数
\[\frac{\partial J_{L1}(w)}{\partial w} \bigg |_{w=0^-} =d_0 - \lambda \\ \frac{\partial J_{L1}(w)}{\partial w} \bigg |_{w=0^-} =d_0 + \lambda \]可见,引入 L2 正则时,代价函数在0处的导数仍是 \(d_0\),无变化。
而引入L1正则后,代价函数在0处的导数有一个突变。从\(d_0 + \lambda\) 到 \(d_0 - \lambda\), 如果\(d_0 + \lambda\) 和\(d_0 - \lambda\)异号,则在0处会是一个极小值点。因此,优化时,很可能优化到该极小值点上,即 \(w=0\) 处。
这里只解释了有一个参数的情况,如果有更多的参数,也是类似的。因此,用L1正则更容易产生稀疏解。
3.4 加入 L2 正则化的结果 当加入L2正则化的时候,分析和L1正则化是类似的,也就是说我们仅仅是从菱形变成了圆形而已,同样还是求原曲线和圆形的切点作为最终解。当然与L1范数比,我们这样求的L2范数的从图上来看,不容易交在坐标轴上,但是仍然比较靠近坐标轴。因此这也就是我们老说的,L2范数能让解比较小(靠近0),但是比较平滑(不等于0)。
综上所述,我们可以看见,加入正则化项,在最小化经验误差的情况下,可以让我们选择解更简单(趋向于0)的解。
参考链接