2520是最小的能够被1到10整除的数。 最小的能够被1到20整除的数是多少? 题目意思: 求1-20之间所有数的最小公倍数。 题目分析: 1.我们知道,多个数之间的最小公倍数,可以使用分解
2520是最小的能够被1到10整除的数。
最小的能够被1到20整除的数是多少?
题目意思:
求1-20之间所有数的最小公倍数。
题目分析:
1.我们知道,多个数之间的最小公倍数,可以使用分解质因数的方法进行。
例如我们要求1,2,3,4,5,6的最小公倍数,先分解质因数
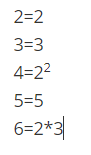
然后,把每个质因子(2,3,5)中,选取最大的一个幂,进行连乘
2中最大的有两次,3中最大的有一次,5中最大的有一次
即:

结果就出来了。
2.方法
首先定义一个数组p[],p[i]用于存放i的质因子数量
那么对于一个数x,我们更新p数组的代码段就如下:
void f(int x){
for(int i=2;;i++){
int cnt=0;//x包含质因子i的个数
while(x%i==0){
x/=i;cnt++;//x包含质因子i
}
p[i]=max(p[i],cnt);//最小公倍数,找最大的一个幂
if(x==1)break;
}
}
因为是找最高的次数,因此每个循环中定义一个计数cnt,用于与现有的p[i]进行比较。
由于质数的性质,分解质因数的代码就是一个for循环(用于枚举数)套一个while循环(用于找出i的个数)。
那么后面的工作就很简单了,对p数组中的东西进行一个相乘+输出就可以了,全部代码如下:
#include<bits/stdc++.h>
using namespace std;
int p[150000];//p[i]表示包含的i质因子个数
void f(int x){
for(int i=2;;i++){
int cnt=0;//x包含质因子i的个数
while(x%i==0){
x/=i;cnt++;//x包含质因子i
}
p[i]=max(p[i],cnt);//最小公倍数,找最大的一个幂
if(x==1)break;
}
}
int g(int x,int y){
int ans=1;
for(int i=1;i<=y;i++)ans*=x;
return ans;
}
int main(){
for(int i=1;i<=20;i++){
f(i);
}
int ans=1;
for(int i=2;i<=150000;i++){
if(p[i]!=0)ans*=g(i,p[i]);
}
printf("%d",ans);
}
附输出结果:232792560
