【BP预测】基于遗传算法优化BP神经网络实现数据预测含Matlab源码

1 简介

为了提高 BP 神经网络预测模型对混沌时间序列的预测准确性, 提出了一种基于遗传算法优化 BP 神经网络的改进混沌时间序列预测方法. 利用遗传算法优化 BP 神经网络的权值和阈值, 然后训练 BP 神经网络预测模型以求得最优解, 并将该预测方法应用到几个典型混沌时间序列和实测短时交通流时间序列进行有效性验证. 仿真结果表明, 该方法对典型混沌时间序列和短时交通流具有较好的非线性拟合能力和更高的预测准确性.

2 部分代码

%%% 清空环境变量
clc
clear all
close all
%%% 设置全局变量
global net inputn outputn inputps outputps output_test input_test;
global inputnum outputnum hiddennum;
%1.3 读取数据格式三：2个输入变量，2个输出变量
TrainData = textread('nanjingxunlian.txt');
TestData = textread('nanjingceshi.txt');
%数据作用处理
input_train=TrainData(1:203,2:6)'; %输入点800行1-4列数据
output_train=TrainData(1:203,1)'; %输出800行第5列数据
input_test=TestData(1:87,2:6)'; %测试用输入数据
output_test=TestData(1:87,1)'; %分析误差用的（准确）期望输出
%1.5 训练样本输入、输出数据归一化
[inputn,inputps]=mapminmax(input_train);%inputn,inputps分别是归一化后的数据和结构体(包含最大值最小值平均数等)
[outputn,outputps]=mapminmax(output_train);
%1.6 BP网络结构
inputnum=5;
hiddennum=3;
outputnum=1;
%%% 第二步： BP网络算法及其均方误差
tBP=cputime;%计时开始
[BPoutput,BPerror,BPmse,BPmape]=BP_ZHY(input_train,output_train,input_test,output_test);
eBP=cputime-tBP;%计时结束，得到建模仿真时间
figure(3)
[r c]=size(BPoutput);
plot([1:c],BPoutput(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('BP网络预测');
title(['BP网络预测']);
figure(4)
[r c]=size(BPerror);
plot([1:c],BPerror(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('BP网络预测误差');
title(['BP网络预测误差曲线']);
%%% 第三步：遗传算法优化BP网络算法及其均方误差
%3.1 遗传算法参数初始化
maxgen=30; %%%留意十二：进化代数，即迭代次数。过大或过小都未必好。可调。
sizepop=10; %%%留意十三：种群规模。可调。
pcross=[0.2]; %%%留意十四：交叉概率选择，0和1之间。可调。
pmutation=[0.05]; %%%留意十五：变异概率选择，0和1之间。可调。
%3.2 遗传算法及其最优个体
[bestchrom,trace] = GABPbestchrom_ZHY(maxgen,sizepop,pcross,pmutation);
%3.3 遗传算法优化BP网络算法及其均方误差
tGB=cputime;%计时开始
[GB_sim,GBerror,GBmse,GBmape] = GABPsim_ZHY(bestchrom,input_test,output_test);
eGB=cputime-tGB;%计时结束，得到建模仿真时间
figure(5)
[r c]=size(GB_sim);
plot([1:c],GB_sim(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('GB网络预测');
title(['GA优化BP网络预测']);
figure(6)
[r c]=size(GBerror);
plot([1:c],GBerror(1,:),'b-');
grid;
axis tight;
xlabel('迭代次数');ylabel('GB网络预测误差');
title(['GA优化BP网络预测误差曲线']);
%%% 第四步：两种算法结果对比分析
figure(7)
[r c]=size(BPerror);
plot([1:c],BPoutput(1,:),'b-',[1:c],GB_sim(1,:),'r-',[1:c],output_test(1,:),'g-');
grid;
axis tight;
xlabel('进化代数');ylabel('预测');
legend('BP网络预测','GA优化BP网络预测','网络期望');
title(['2算法网络预测比较']);
figure(8)
[r c]=size(BPerror);
plot([1:c],BPerror(1,:),'b-',[1:c],GBerror(1,:),'r-');
grid;
axis tight;
xlabel('进化代数');ylabel('误差');
legend('BP预测误差','GA优化BP预测误差');
title(['误差曲线']);
figure(9)
[r c]=size(BPerror);
plot( [1:c],BPmape(1,:),'b-',[1:c],GBmape(1,:),'r-');
grid;
axis tight;
xlabel('进化代数');ylabel('百分比误差');
legend('BP预测百分比误差','GA优化BP预测百分比误差');
title(['误差曲线']);
disp(['BP建模仿真时间为：' num2str(eBP) 's'] );
disp(['GA优化后BP再建模仿真时间为：' num2str(eGB) 's'] );
disp(['BP均方误差为：' num2str(BPmse)] );
disp(['GA优化BP均方误差为：' num2str(GBmse)] );

3 仿真结果

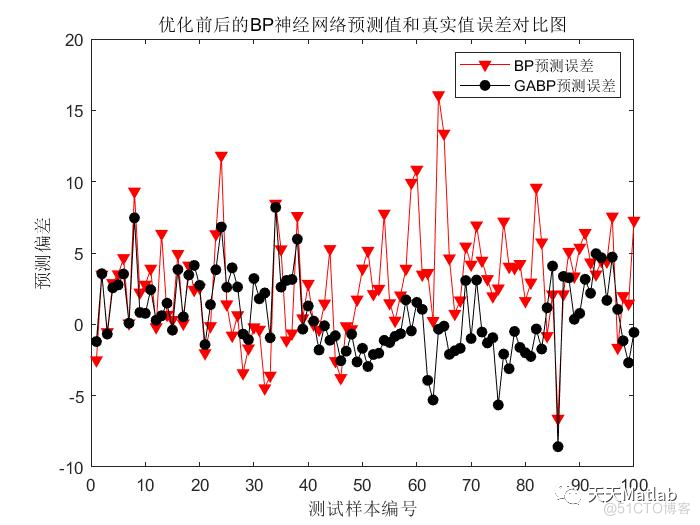
4 参考文献

[1]梁毅, and 刘世洪. "基于遗传算法优化的BP神经网络的组合预测模型方法研究." 中国农业科学 45.023(2012):4924-4930.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。