机器学习的可解释性
- 1.可解释性简介
- 2.可解释性的重要性
- 3.可解释模型具体技术
- 3.1 Permutation Importance
- 3.2 Partial Dependency Plots
- 3.3 SHAP
- 3.4 SHAP Values 的高级用法
1.可解释性简介
理解(interpret)表示用可被认知(understandable)的说法去解释(explain)或呈现(present)。在机器学习的场景中,可解释性(interpretability)就表示模型能够使用人类可认知的说法进行解释和呈现。

机器学习模型被许多人称为“黑盒”。 这意味着虽然我们可以从中获得准确的预测,但我们无法清楚地解释或识别这些预测背后的逻辑。 但是我们如何从模型中提取重要的见解呢? 要记住哪些事项以及我们需要实现哪些功能或工具? 这些是在提出模型可解释性问题时会想到的重要问题。
想象一下,在工作中如何跟业务的领导讲解自己的模型呢,他们可是对计算机可能没有任何背景的,如何让领导能够更好的理解,自己做的算法模型,有用
2.可解释性的重要性
为什么模型给出预测结果了还不满意,还要这么执意于知道模型是如何做出预测的?这和模型在真实世界中产生的影响有很大关系。对于仅仅被用来做电影推荐的模型而言,其影响性相较于做药物效果预估所使用的模型要小得多。
问题在于一个单一指标,就好比分类准确率,是不足以刻画真实世界中的大部分问题的。
这里有一个可解释机器学习的大框架。在某种程度上,我们通过从真实世界(World)中获取一些原始数据(Data),并用这这些数据进行更深入的预测分析(Black Box Model)。而模型的解释性方法(Interpretability)只是在模型之上增加了一层,以便于人们(Humans)更好地理解预测过程。
以下是一些由可解释性带来的好处:
- 可靠性
- 易于调试
- 启发特征工程思路
- 指导后续数据搜集
- 指导人为决策
- 建立信任
3.可解释模型具体技术
想要更好的理解一个模型,需要知道以下内容:
- 模型中最重要的特征
- 对于每一次预估决策,不同特征变量发挥的作用
- 每个特征在使用大量数据进行预估时发挥的作用
具体技术有:
3.1 Permutation Importance
对于模型来说,哪一个特征才是最重要的?哪一个特征对于模型做决策有更大的影响?这个概念被称为特征重要度,而Permutation Importance正是目前被广泛采用计算特征重要度的方式。当我们的模型预测出了难以理解的结果时,我们可以通过这个指标来知道到底发生了什么。当然,如果我们需要向别人解释自己模型的预测时也可以用这种方法。
Permutation Importance对很多scikit-learn中涉及到的预估模型都有用。其背后的思想很简单:随机重排或打乱样本中的特定一列数据,其余列保持不变。如果模型的预测准确率显著下降,那就认为这个特征很重要。与之对应,如果重排和打乱这一列特征对模型准确率没有影响的话,那就认为这列对应的特征没有什么作用。
使用方法
试想我们现在做了一个预测足球队里谁会获得“足球先生”称号的模型,并且该模型并不是几个简单参数就能刻画的。当然,只有表现最好的球员才能获得此称号。
Permutation Importance是在模型完成拟合之后才进行计算的。所以,我们先用RandomForestClassifier在训练样本上拟合出一个分类模型,我们不妨称之为my_model。
我们使用ELI5库可以进行Permutation Importance的计算。ELI5是一个可以对各类机器学习模型进行可视化和调试Python库,并且针对各类模型都有统一的调用接口。ELI5中原生支持了多种机器学习框架,并且也提供了解释黑盒模型的方式。
通过eli5库来计算并展示特征重要度:
import eli5from eli5.sklearn import permutationImportance
perm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist())
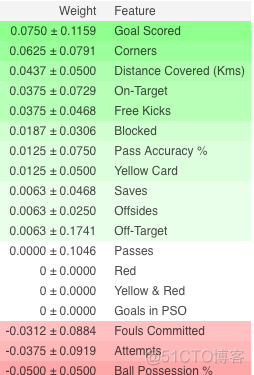
模型解释
- 最上面的特征是最重要的特征,最下面则是最不重要的特征。在这个case中,进球数(Goal Scored)是最重要的特征。
- ±后面的数字表示多次随机重排之间的差异值
- 有些特征重要度权重是负数,表示随机重排这些特征之后,模型的表现甚至更好了
3.2 Partial Dependency Plots
Partial Dependency Plots(后续用PDP或PD简称)会展示一个或两个特征对于模型预测的边际效益(J. H. Friedman 2001)。PDP可以展示一个特征是如何影响预测的。与此同时,我们可以通过绘制特征和预测目标之间的一维关系图或二维关系图来了解特征与目标之间的关系。
使用方法
PDP也是在模型拟合完成之后开始计算的。用刚刚足球球员的例子来说,模型使用了很多特征,类似传球数、射门次数、进球数等等。我们从中抽取一个样本球员来进行说明,比如该球员占全队50%的持球时长、传球过100次、射门10次并进球1次。
我们先训练模型,然后用模型预测出该球员获得“足球先生”的概率。然后我们选择一个特征,并变换球员该特征值下的特征输入。比如我们调整刚刚抽取的那名球员,将其进球数分别设置成一次、两次、三次,然后画出预测概率随着进球数变化的走势图。
from matplotlib import pyplot as pltfrom pdpbox import pdp, get_dataset, info_plots
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=my_model, dataset=val_X, model_features=feature_names, feature='Goal Scored')
# plot it
pdp.pdp_plot(pdp_goals, 'Goal Scored')
plt.show()
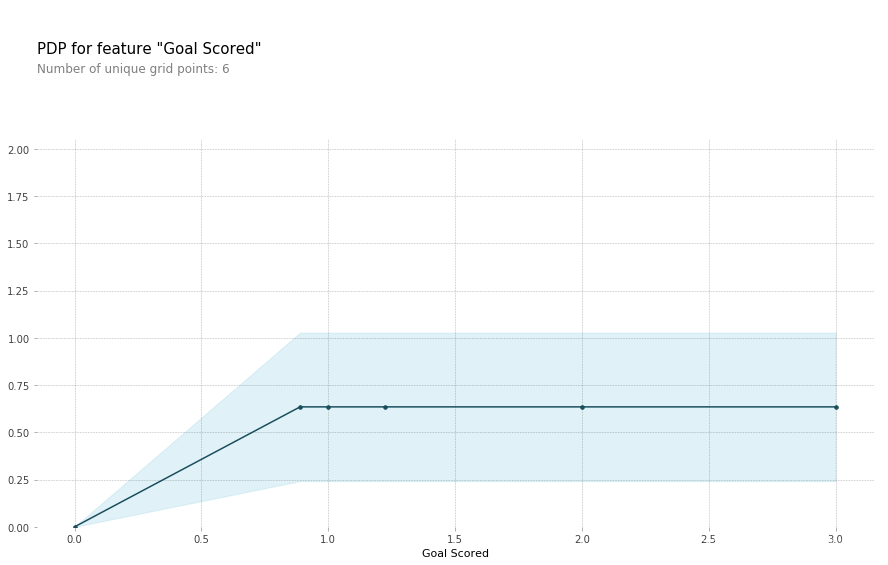
模型解释
- Y轴表示预测相较于基准线或最左值的增加值
- 蓝色区域表示置信区间
- 从上图针对进球数的PDP分析看,随着进球数增多,球员获得“足球先生”的概率也会逐步增加,但增加到一定程度之后就收敛了。
我们同样可以使用二维图上画出针对两个特征的PDP分析图:
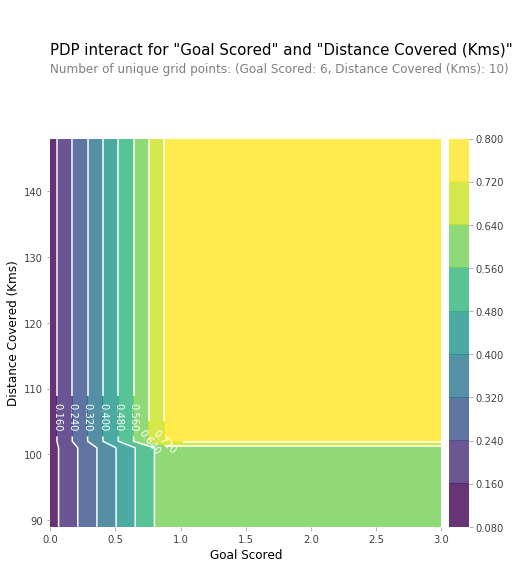
3.3 SHAP
SHAP(SHapley Additive exPlanation)有助于细分预测以显示每个特征的影响。 它基于Shapley values,这是一种用于博弈论的技术,用于确定协作游戏中每个玩家促成其成功的贡献有多少¹。 通常情况下,在准确性和可解释性之间取得正确的权衡可能是一个困难的平衡行为,但SHAP值可以同时提供这两者。
操作方法:再一次,以足球为例,我们想要预测一个球队有一名球员赢得“最佳球员”的概率。SHAP values解释了给定特性具有特定值的影响,并与我们在该特性具有某些基线值时所做的预测进行比较。
SHAP values 使用Shap库进行计算。从PyPI或conda安装Shap 库很简单
Shap值显示给定的特性对我们的预测有多大的改变(与我们在该特性的某个基线值上进行预测相比)。假设我们想知道当球队进了3个球而不是某个固定的底线时预测是什么。如果我们能够解决这个问题,我们可以对其他功能执行相同的步骤如下:
sum(SHAP values for all features) = pred_for_team - pred_for_baseline_values因此,预测可以分解为如下图:

模型解释
上面的解释显示了推动模型输出从基本值(我们传递的训练数据集中的平均模型输出)到模型输出的每个特性。将预测推高的特征用红色表示,将预测推低的特征用蓝色表示 。
- 这里的base_value是0.4979,而我们的预测值是0.7。
- 得分= 2对预测增加的影响最大,
- 而控球率对预测减少的影响最大。
3.4 SHAP Values 的高级用法
聚合许多SHAP Values有助于更详细的了解模型。
- SHAP 摘要图绘制
为了了解模型中哪些特性最重要,我们可以为每个示例绘制每个特性的SHAP values 。摘要图说明哪些特性是最重要的,以及它们对数据集的影响范围。
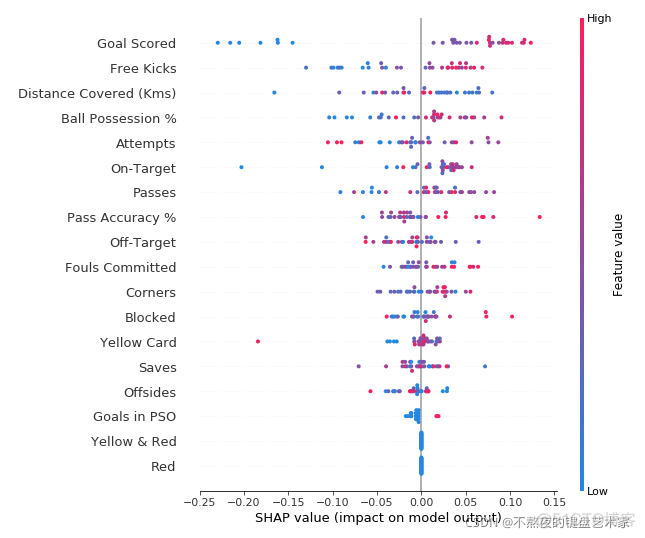
关于每个点:
- 垂直位置显示了它所描述的特征
- 颜色显示数据集中这一行的特征值是高还是低
- 水平位置显示该值的影响是导致较高的预测还是较低的预测。
左上方的点是一个进球很少的球队,预测降低了0.25。
- SHAP Dependence Contribution图
虽然SHAP摘要图给出了每个特性的一般概述,但是SHAP dependence图显示了模型输出如何随特性值而变化。SHAP dependence contribution图提供了与PDP类似的见解,但添加了更多的细节。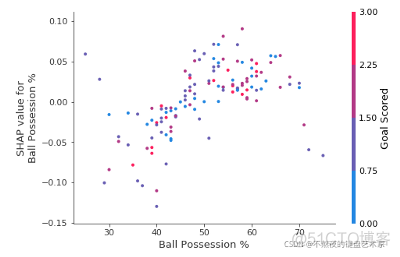
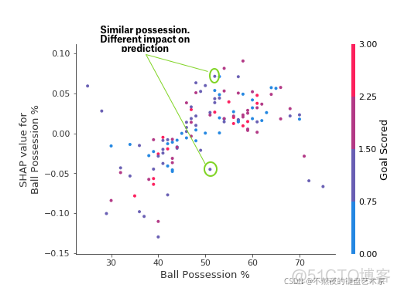
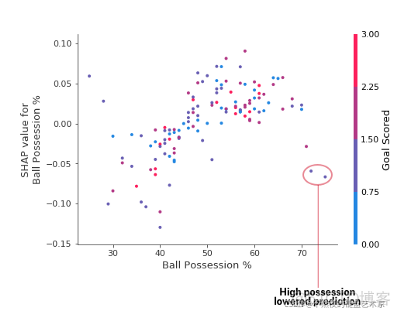
上述依赖性贡献表明,拥有球会增加球队让球员赢得奖励的机会。 但如果他们只得到一个进球,那么这个趋势就会逆转而且如果他们得分那么少,那么裁判可能会因为得分而惩罚他们。
