NC16884 [NOI2001]食物链

题目链接

题目

题目描述

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B，B吃C，C吃A。

现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这N个动物所构成的食物链关系进行描述：

第一种说法是“1 X Y”，表示X和Y是同类。

第二种说法是“2 X Y”，表示X吃Y。

此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

1） 当前的话与前面的某些真的话冲突，就是假话；

2） 当前的话中X或Y比N大，就是假话；

3） 当前的话表示X吃X，就是假话。

你的任务是根据给定的N（1≤N≤50,000）和K句话（0≤K≤100,000），输出假话的总数。

输入描述

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

输出描述

只有一个整数，表示假话的数目。

示例1

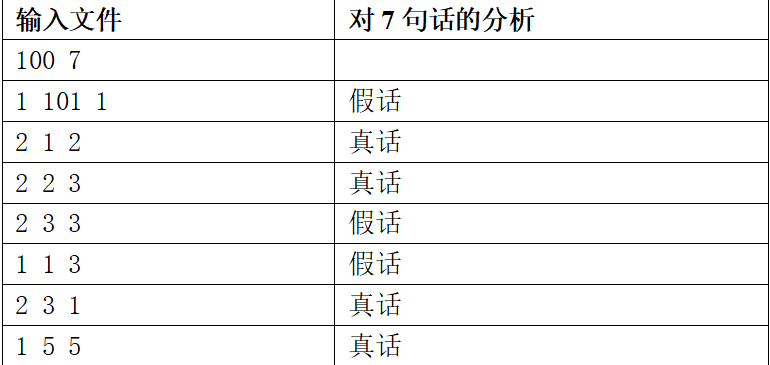
输入

100 7
1 101 1   
2 1 2     
2 2 3     
2 3 3     
1 1 3     
2 3 1     
1 5 5

输出

3

说明

题解 方法一

知识点：并查集。

用权值代表其关于根节点的种类，根节点设为 \(0\) ，其他的同类为 \(0\) ，根节点是猎物为 \(1\) ，根节点是天敌为 \(2\) 。

因为种类形成环状具有传递性关系，因此路径压缩可以利用自身权值加父节点路径压缩后的权值对 \(3\) 取模即可，递归实现。

合并集合时，已知两个节点 \(a\) 和 \(b\) 路径压缩后的权值以及\(a\) 关于 \(b\) 的权值，要求出集合根节点 \(A\) 认 \(B\) 为父后的权值，因为具有环状传递性，所以可以利用向量的思想，\(\vec{AB} = -\vec{aA}+\vec{ab}+\vec{bB}\) ，随后对 \(|\vec{AB}|\) 模 \(3\) 即可，注意不要出现负数。

如果给出的关系的两个对象已经在同一个关系集合，那么检查他们关系是否和给出的条件吻合，即 \(\vec{ab} == \vec{aA} - \vec{bA}\) ，左边是条件右边是已有的关系，不吻合的答案加一。

时间复杂度 \(O(k\log n + n)\)

空间复杂度 \(O(n)\)

方法二

知识点：并查集。

实际上第一种解法较为繁琐，我们只关心条件之间是否矛盾，即给出的条件的两个对象已经建立了关系，检测已有关系和给出的关系是否矛盾。因此可以用扩展域并查集，其把元素的所有可能种类扩展各个独立元素，只对有具体种类的元素建立关系集合中的具体等价类（等价类的元素会同时出现），而不把相关的具体等价类并在一个集合产生完整的关系集合，利用权值进行相对分类（带权并查集是记录了一整个关系集合，并用权值做了相对根节点的关系划分），而这对于检测矛盾已经足够了。

具体地说，一个动物元素只有三种种类，我们记为 \(A\)，\(B\)，\(C\)，其中 \(A\) 吃 \(B\) ， \(B\) 吃 \(C\) ， \(C\) 吃 \(A\) 。扩展域并查集把每个动物元素扩展成这 \(3\) 个有具体种类的动物元素，分别放在 $[1,n],[n+1,2n],[2n+1，3n] $ 中。

假设给出 \(a\) 吃 \(b\)，则会合并三个等价类 \([a]\) 与 \([b+n]\) ， \([a+n]\) 与 \([b+2n]\) ， \([a+2n]\) 与 \([b]\) ，表示 \(a\) 是 \(A\) 时 \(b\) 一定是 \(B\)， \(a\) 是 \(B\) 时 \(b\) 一定是 \(C\)，\(a\) 是 \(C\) 时 \(b\) 一定是 \(A\) ，这样就根据条件合并了两个对象的三组具体种类的等价类。注意一个条件一定能合并三组等价类，因为这三个等价类是一个关系集合的三个具体种类表现，同样的一个等价类出现一定有其余两个等价类，且他们种类刚好补全所有情况。比如， \([a] = [b]\) 出现则一定有 \([a+n] = [b+n]\) 和 \([a+2n] = [b +2n]\)，因为他们是一个同一个相对关系（同类）的三个具体表现。

另一方面，对于 \(a\) 吃 \(b\) 的条件，如果它们已经在一个关系集合（已有相对关系），则它们之间一定产生了三个等价类，而如果这些等价类刚好是 \([a] = [b]\) 或者 \([a] = [b+2n]\) ，即表达 \(a\) 与 \(b\) 同类或者 \(a\) 的天敌是 \(b\) 就很容易判断出已知条件与给出的这个条件矛盾。

因此，扩展域并查集能够维护元素不同种类之间同时出现的集合，即等价类，容易直接判断出条件是否矛盾。但弊端也很明显，只适合检验某个条件相对关系是否满足现有关系，而不能直接列举出元素的相对关系，因为扩展域并查集只保存了元素具体种类的等价关系，而没有完整记录元素在关系集合中的相对关系，导致等价类之间是割裂的，没有直接相关性的。比如我想要知道动物 \(a\) 和 动物 \(b\) 的相对关系，就得先拿 \(a\) 的某个种类所在的等价类集合作为一个基准集合，再枚举 \(b\) 的所有种类(\(A,B,C\))是否处在这个基准集合，如果有关系则有且仅有一个具体种类处在基准集合进而判断其相对关系，而都没有处在基准集合说明 \(a\) 和 \(b\) 尚未建立关系。这个过程带权并查集能在合并和查询过程中直接实现，因此如果题目要求并不是检验条件矛盾这么简单的话，比如要求得知 \(a\) 和 \(b\) 的相对关系用以后续解题，那带权并查集会更加合适。

时间复杂度 \(O(k\log n + n)\)

空间复杂度 \(O(n)\) ，实际上是三倍空间

代码 方法一

#include <bits/stdc++.h>

using namespace std;

inline int read() {
    int x = 0, f = 1;char c = getchar();
    while (c < '0' || c>'9') { if (c == '-') f = -1;c = getchar(); }///整数符号
    while (c >= '0' && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48);c = getchar(); }///挪位加数
    return x * f;
}

int fa[50007], dist[50007];

int find(int x) {
    if (fa[x] != x) {
        int pre = fa[x];
        fa[x] = find(pre);
        dist[x] = (dist[x] + dist[pre]) % 3;
    }
    return fa[x];
}

bool merge(int x, int y, int op) {
    int rx = find(x);
    int ry = find(y);
    int delta = (dist[x] - dist[y] + 3) % 3;
    if (rx == ry) return delta == op;
    fa[rx] = ry;
    dist[rx] = (op - delta + 3) % 3;
    return true;
}

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n = read(), k = read();
    for (int i = 1;i <= n;i++) fa[i] = i;
    int ans = 0;
    while (k--) {
        int op = read(), x = read(), y = read();
        op--;
        if (x > n || y > n) ans++;
        else if (!merge(x, y, op)) ans++;
    }
    cout << ans << '\n';
    return 0;
}

方法二

#include <bits/stdc++.h>

using namespace std;

inline int read() {
    int x = 0, f = 1;char c = getchar();
    while (c < '0' || c>'9') { if (c == '-') f = -1;c = getchar(); }///整数符号
    while (c >= '0' && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48);c = getchar(); }///挪位加数
    return x * f;
}

int fa[150007];

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y) {
    fa[find(x)] = find(y);
}

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n = read(), k = read();
    for (int i = 1;i <= 3 * n;i++) fa[i] = i;
    int ans = 0;
    while (k--) {
        int op = read(), x = read(), y = read();
        if (x > n || y > n)ans++;
        else if (op == 1) {
            if (find(x) == find(y + n) || find(x) == find(y + 2 * n)) ans++;
            else merge(x, y), merge(x + n, y + n), merge(x + 2 * n, y + 2 * n);
        }
        else if (op == 2) {
            if (find(x) == find(y + 2 * n) || find(x) == find(y)) ans++;
            else merge(x, y + n), merge(x + n, y + 2 * n), merge(x + 2 * n, y);
        }
    }
    cout << ans << '\n';
    return 0;
}