排序算法之——堆排序分析

前言

上一篇文章中对堆进行了分析，接下来趁热打铁，一起来学习一下堆排序算法。

思路

回忆建立N个元素的二叉堆的基本策略，这个阶段花费时间，然后我们执行N次​​​deleteMin​​​操作，按照顺序，最小
的元素先离开堆，离开之后，我们让堆缩小1，位于堆中最后的单元就可以用来存放刚刚删除的元素。这样可以得到逆序排序。
为了得到正序排序，我们用大顶堆即可，每次把堆中最大的元素删除。

有点类似选择排序的思想，右侧都是已经排好序的，不停的从左侧选择最小者加入右侧。

假设输入序列：[59, 7, 19, 43, 77, 52, 91]

最后得到的的堆序列：[91, 77, 59, 43, 7, 52, 19]

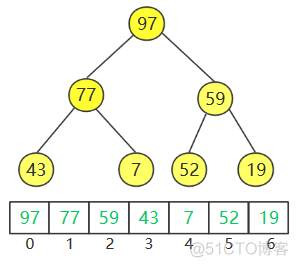
执行删除操作，如下图所示，虚线代表节点已经不属于堆了。97放到最后的位置，

堆大小减1，现在该堆只包含6个元素。数组中蓝色边框表示右侧已经排好序的数列。

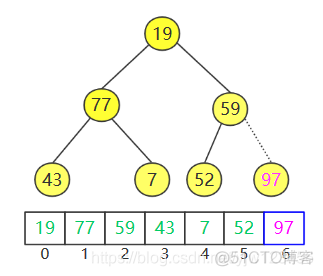
但此时还需要对19进行下滤操作，下滤完成后如图：

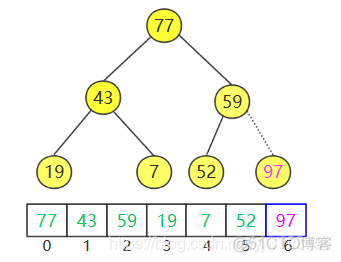
继续删除77，并进行下滤：

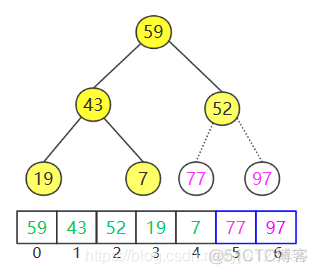
继续删除59，并进行下滤：

注意最后一个节点是7而不是52。

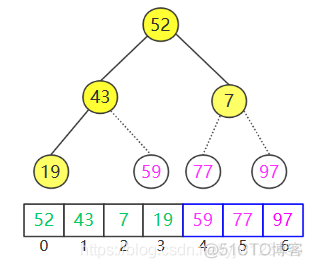
继续删除52，并下滤：

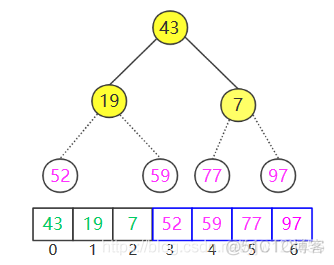
继续删除43，并下滤(数据量是不是太大了，还没画完。。。)：

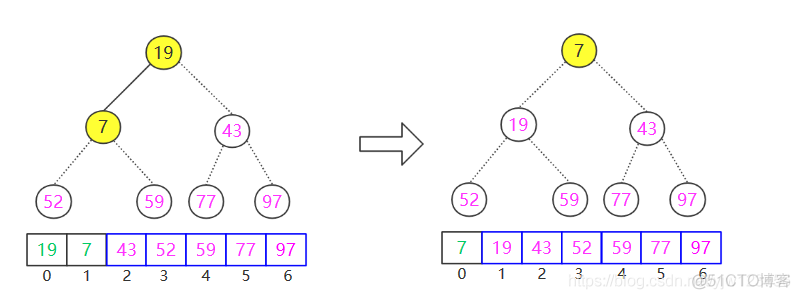
上面是删除了19的结果，可以看到，此时堆中仅剩一个节点，但是已经不需要进行任何操作了，因为该节点必然是最小的。这一点可以在代码中体现出来。

代码

/**
* 通过Max堆实现堆排序，堆排序的数组包含0处的位置
* @param array
* @param <E>
*/
public static <E extends Comparable<? super E>> void heapSort(E[] array) {

//因为包含索引0处的位置，最后内部节点的计算也不一样
//首先是建堆
for (int i = array.length/2 - 1;i >= 0; i--) {
percDown(array,i,array.length);
}

for (int i = array.length - 1; i > 0; i--) {//为啥不是i>=0? 因为当i为1时，此时堆中仅剩一个节点，但是已经不需要进行任何操作了
swap(array,0,i);//因为大顶堆中最大元素位置一定是堆顶，0的位置 ，每次交换堆顶和最后一个元素的位置
percDown(array,0,i);//所需处理的长度刚好也是i
}
}

private static <E extends Comparable<? super E>> void percDown(E[] array,int hole,int size) {
int child;
E tmp = array[hole];
while ((hole * 2 + 1) < size) {
//如果有孩子，hole不停的往下
child = hole * 2 + 1;
//若有右孩子，且右孩子更大
if (child != size -1 &&
array[child].compareTo(array[child + 1]) < 0) {
child++;//取右孩子
}
//如果tmp小于孩子节点的值
if (tmp.compareTo(array[child]) < 0) {
//hole位置填充最大孩子节点的值
array[hole] = array[child];
hole = child;//继续比较
} else {
break;
}
}
array[hole] = tmp;
}

private static <E> void swap(E[] array,int i,int j) {
E tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}

注意，当数组下标从0开始时，计算：

• 左节点：​​i * 2 + 1​​
• 右节点：​​i * 2 + 2​​
• 有孩子：​​i * 2 + 1 < 堆大小​​
• 有右孩子：​​i * 2 + 1 != 堆大小 - 1​​

复杂度和稳定性

• 时间复杂度

堆排序是一种选择排序，整体主要由构建初始堆加上交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经复杂度为，在交换并重建堆的过程中，需交换次，而重建堆的过程中，根据完全二叉树的性质，逐步递减，近似为。所以堆排序时间复杂度就是级。

• 稳定性

堆排序是不稳定的算法。它在交换数据的时候，是比较父结点和子节点之间的数据，所以，即便是存在两个数值相等的兄弟节点，它们的相对顺序在排序也可能发生变化。