深入剖析多重背包问题（上篇）

在本篇文章当中主要跟大家介绍了多重背包的两种解决办法，一种是将多重背包转化成01背包，另外一种方法是根据多重背包的动态转移方程去解决问题。 深入剖析多重背包问题（上篇） 前言

在前面的两篇文章当中，我们已经仔细的讨论了01背包问题和完全背包问题，在本篇文章当中将给大家介绍另外一种背包问题——多重背包问题，多重背包问题的物品数量介于01背包问题和完全背包问题之间，他的物品的数量是有限个！

多重背包问题介绍

有 \(N\) 种物品和一个容量是 \(V\) 的背包。第 \(i\) 种物品最多有 \(s_i\) 件，每件体积是 \(v_i\)，价值是 \(w_i\)。求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。

注意：上面使用到的字符含义在本篇文章当中都一样。

多重背包问题跟01背包和完全背包的区别都是在物品的可用次数上，01背包只能使用一次，多重背包可以使用无数次，而多重背包可以使用多次。

背包问题复习——01背包的动态转移方程 01背包的动态转移方程

01背包问题当中，我们是使用一个二维数组dp[i][j]进行计算，dp[i][j]表示在只使用前i个物品且背包容量为j的情况下，我们能够获得的最大的收益。在这个情况下，我们根据当前背包容量j判断是否能装入第i个物品可以得到下面两个方程：

\[dp[i][j] = \begin{cases} max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]), j \ge v[i]\\ dp[i - 1][j] , j \lt v[i] \end{cases} \]

上面01背包的公式的第二条比较简单，如果背包容量不足以容纳第i件物品，那么只能从前i - 1物品当中选择了。我们来仔细分析一下第一条公式。

如果当前背包容量可以容纳第i个物品，那么我们就可以选择第i件物品或者不选择，我们应该选择两种选择当中收益更大的那个。

• 如果我们不选择第i个物品，那么我们就能够使用容量为j的背包去选择前i - 1个物品，这种情况下我们的最大收益为dp[i - 1][j]。
• 如果选择第i个物品，那么我们背包容量还剩下j - v[i]，还可以选择剩下的i - 1个物品，而且我们的收益需要加上w[i]，因此我们的收益为max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j])。

将多重背包转化成01背包

在多重背包的问题当中，我们对于一种物品我们可以使用多次，比说\(A\)物品我们可以用三次。事实上我们可以将多重背包转化成01背包，比如我们可以将三个\(A\)物品变成三个不同的物品，所谓不同就是他们的名字不一样，但是他们的价值和体积都是一样的，假设\(A\)的体积为\(V_a\)，价值为\(W_a\)，能够使用的次数为3次，那么我们可以将其转化成\(A_1\)，\(A_2\)，\(A_3\)，这三个物品的体积和价值均为\(V_a\)和\(W_a\)，这样的话\(A\)可以使用3次就转化成了\(A_1\)、\(A_2\)和\(A_3\)均只能使用一次。通过这种转换我们就将多重背包转化成了01背包。

多重背包Java代码：

import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int V = scanner.nextInt();
        ArrayList<Integer> v = new ArrayList<>();
        ArrayList<Integer> w = new ArrayList<>();
        for (int i = 0; i < N; i++) {
            int vi = scanner.nextInt();
            int wi = scanner.nextInt();
            int t = scanner.nextInt();
            for (int j = 0; j < t; j++) {
                v.add(vi);
                w.add(wi);
            }
        }
        int[][] dp = new int[v.size() + 1][V+ 1];

        // 对第0行进行初始化操作
        for (int i = v.get(0); i <= V; ++i) {
            dp[0][i] = w.get(0);
        }

        for (int i = 1; i < v.size(); ++i) {
            for (int j = 0; j <= V; ++j) {
                if (j >= v.get(i)) {
                    dp[i][j] = Math.max(dp[i - 1][j],
                                        dp[i - 1][j - v.get(i)] + w.get(i));
                }
                else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        System.out.println(dp[v.size() - 1][V]);
    }
}

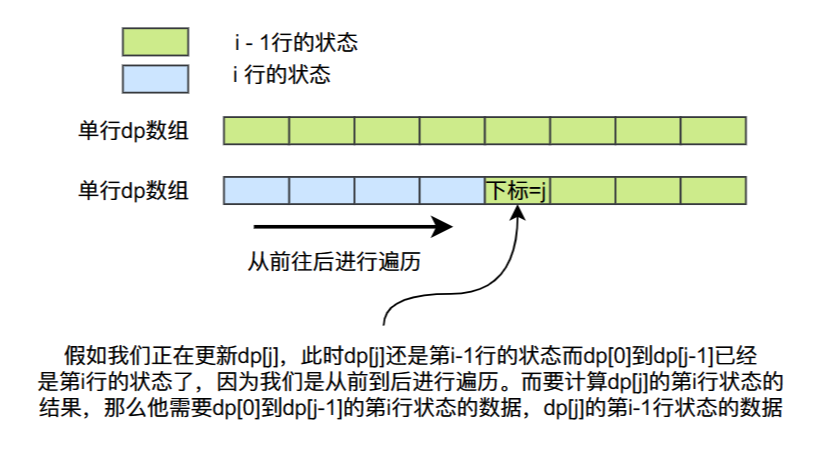
和01背包一样，我们对多重背包也可以使用单行数组进行优化：

import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int V = scanner.nextInt();
        ArrayList<Integer> v = new ArrayList<>();
        ArrayList<Integer> w = new ArrayList<>();
        for (int i = 0; i < N; i++) {
            int vi = scanner.nextInt();
            int wi = scanner.nextInt();
            int t = scanner.nextInt();
            for (int j = 0; j < t; j++) {
                v.add(vi);
                w.add(wi);
            }
        }
        int[] f = new int[V + 1];
        for (int i = 0; i < v.size(); i++) {
            for (int j = V; j >= v.get(i); j--) {
                f[j] = Math.max(f[j], f[j - v.get(i)] + w.get(i));
            }
        }
        System.out.println(f[V]);
    }
}

多重背包动态转移方程

在背包容量足够的情况下，01背包的动态转移方程为：

\[dp[i][j] = max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]), j \ge v[i] \]

上述的动态转移方程是基于每个物品选和不选，那么对于多重背包来说，如果物品可以选择\(S\)次，我们可以选择0次，可以选择1次，......，可以选择\(S\)次，我们就需要从这些情况当中选择收益最大的那次（前提是背包能够容纳下相应次数的物品），因此多重背包的动态转移方程如下（ \(T = min(S, \frac{V}{v_i})\)，其中\(S\)表示物品能够选择的次数，\(v_i\)表示物品的体积，\(V\)表示当前背包的容量）：

\[dp[i][j] = max\\ \{ \\ dp[i - 1][j], \\ dp[i - 1][j - v[i]] + w[i],\\ dp[i - 1][j - v[i] * 2] + w[i] * 2, \\ ..., \\ dp[i - 1][j - v[i] * T] + w[i] * T\\ \} \]

基于上面的动态转移方程我们可以得到下面的代码：

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int V = scanner.nextInt();
        int[] w = new int[N];
        int[] v = new int[N];
        int[] t = new int[N];
        int[] f = new int[V + 1];
        for (int i = 0; i < N; i++) {
            v[i] = scanner.nextInt();
            w[i] = scanner.nextInt();
            t[i] = scanner.nextInt();
        }
        for (int i = 0; i < N; i++) {
            for (int j = V; j >= v[i]; --j) {
                // 这个循环就表示多重背包的动态转移公式了
                // 在这段代码当中虽然 Math.max的参数只有量
                // 但是有一段循环，将这个循环展开，他表示的
                // 就是多重背包的动态转移方程
                for (int k = 1; k <= t[i] && j >= v[i] * k; k++) {
                    f[j] = Math.max(f[j], f[j - v[i] * k] + w[i] * k);
                }
            }
        }
        System.out.println(f[V]);
    }
}

总结

在本篇文章当中主要跟大家介绍了多重背包的两种解决办法，一种是将多重背包转化成01背包，另外一种方法是根据多重背包的动态转移方程去解决问题，可以看出后者的空间复杂度更低，更节约内存空间。下期我们用另外一种方法去优化多重背包。

以上就是本篇文章的所有内容了，希望大家有所收获，我是LeHung，我们下期再见！！！

---

更多精彩内容合集可访问项目：https://github.com/Chang-LeHung/CSCore

关注公众号：一无是处的研究僧，了解更多计算机（Java、Python、计算机系统基础、算法与数据结构）知识。