AtCoder Beginner Contest 260 G // imos（累积和算法）

题目传送门：G - Scalene Triangle Area (atcoder.jp)

题意：

给定大小为N*N的OX矩阵，若矩阵的(s，t)处为O，其覆盖范围为：满足以下条件的所有位置（i，j）

• s <= i && t <= j

• (i - s) + (j - t) / 2 < M

再给出Q次询问，对于每次询问（x，y），要求给出对应位置被覆盖了多少次。

思路：imos

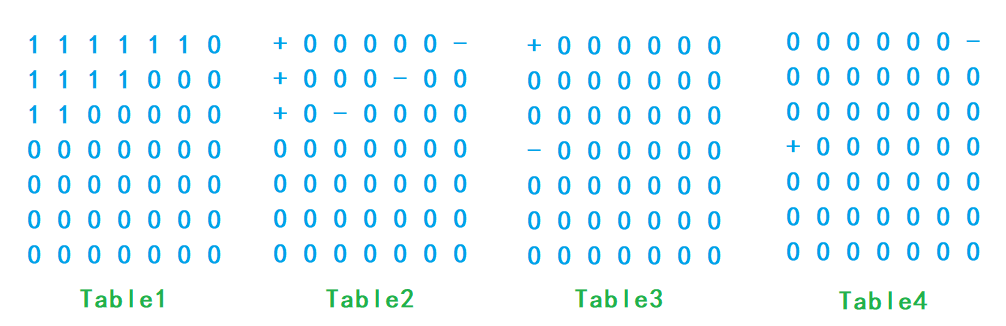
不妨先考虑 n = 7, m = 3, 且仅在左上角处为 'O' 。那么矩阵上每个位置被覆盖次数如Table1所示。

于是我们可以在Table2中，+号处+1，-号处-1，再对每行，进行横向累积和。

• 考虑Table2的+：可以将其进一步化成Table3所示，则进行纵向累积和后，就回到Table2。

• 考虑Table2的-：可以将其进一步化成Table4所示，对其进行纵向累积和时：del [ i ] [ j ] = del [ i ] [ j ] + del [ i - 1 ] [ j - 2 ]，纵向累计和后就回到Table2。

 

一般情况时，也是如此处理，即可得到答案。

复杂度：O(N² + Q).

代码参考：

#include <bits/stdc++.h>
using namespace std;

const int N = 2022;

int n, m, add[N][5 * N], del[N][5 * N];
char g[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        scanf("%s", g[i] + 1);
        for(int j = 1; j <= n; j++)
            if(g[i][j] == 'O')
            {
                ++ add[i][j], -- add[min(i + m, n + 1)][j];
                -- del[i][j + 2 * m], ++ del[min(i + m, n + 1)][j];
            }
    }

    //纵向累积和
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n + 2 * m; j++) add[i][j] += add[i - 1][j], del[i][j] += del[i - 1][j + 2];

    //横向累积和
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++) add[i][j] += add[i][j - 1], del[i][j] += del[i][j - 1];
    
    int Q;
    cin >> Q;
    while(Q--)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        printf("%d\n", add[x][y] + del[x][y]);
    }

    return 0;
}