完美正方形（DFS）

标题：完美正方形：如果一些边长互不相同的正方形，可以恰好拼出一个更大的正方形，则称其为完美正方形。

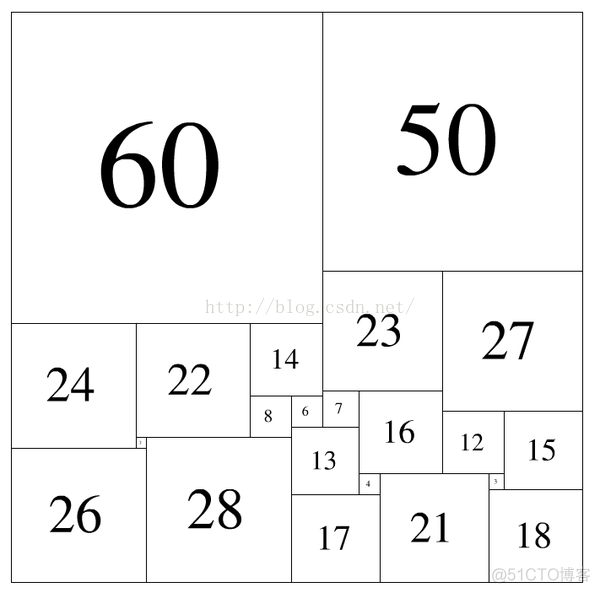
比如：如下边长的22个正方形

2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60

如图那样组合，就是一种解法。此时，

紧贴上边沿的是：60 50

紧贴下边沿的是：26 28 17 21 18

22阶完美正方形一共有8种。下面的组合是另一种：

2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61

如果告诉你该方案紧贴着上边沿的是从左到右依次为：47 46 61，

你能计算出紧贴着下边沿的是哪几个正方形吗？

请找出紧贴着下边沿的正方形的边长，从左到右，用空格分开。

思路：

在N = 47 + 46 + 61的正方形中枚举以每个格点作为某一小正方形的左上角，直到边长N的正方形被这22个小正方形填满为止。

过程需要一个剪枝优化一下：在枚举每个格点作为某一小正方形的左上角时，先将这22个小正方形从小到大排序，

然

后依次填充没有用过的小正方形，当填充失败时（亦即和其他小正方形覆盖或者出界），那么就不需要继续往边长更

大的小正形枚举了。

搜出答案以后，自己写了个judge检验了一下答案的确可行。

#include <cstdio>
#include <algorithm>
#include <set>
#include <iostream>
using namespace std;

const int N = 47 + 46 + 61;
int mp[N + 10][N + 10];
int a[19] = {2, 5, 9, 11, 16, 17, 19, 21, 22, 24, 26, 30, 31, 33, 35, 36, 41, 50, 52};
bool ok(int x, int y, int l) {
if(x + l - 1 > N || y + l - 1 > N) return false;
for(int i = x; i <= x + l - 1; i ++)
for(int j = y; j <= y + l - 1; j ++) {
if(mp[i][j]) return false;
}
return true;
}
bool vis[19];
bool DFS(int x, int y) {
if(x == N + 1 && y == 1) return true;
if(mp[x][y]) {
int nx = x, ny = y + 1;
if(ny == N + 1) nx = x + 1, ny = 1;
return DFS(nx, ny);
}
for(int i = 0; i < 19; i ++) {
if(vis[i]) continue;
int l = a[i];
if(ok(x, y, l)) {
for(int j = x; j <= x + l - 1; j ++)
for(int k = y; k <= y + l - 1; k ++)
mp[j][k] = l;
int nx = x, ny = y + 1;
if(ny == N + 1) nx = x + 1, ny = 1;
vis[i] = 1;
if(DFS(nx, ny)) return true;
vis[i] = 0;
for(int j = x; j <= x + l - 1; j ++)
for(int k = y; k <= y + l - 1; k ++)
mp[j][k] = 0;
} else break;
}
return false;
}

bool book[100];
bool is_ok(int x, int y) {
int l = mp[x][y];
for(int i = x ; i <= x + l - 1; i ++)
for(int j = y; j <= y + l - 1; j ++)
if(mp[i][j] != mp[x][y]) return false;
return true;
}
int vs[N];
bool judge() {
puts("此正方形为：");
vs[47] = 0, vs[46] = 1, vs[61] = 2;
for(int i = 0; i < 19; i ++) vs[a[i]] = 3 + i;
for(int i = 1; i <= N; i ++, puts(""))
for(int j = 1; j <= N; j ++) printf("%c", 'a' + vs[mp[i][j]]);
set<int> alledge;
alledge.insert(47);
alledge.insert(46);
alledge.insert(61);
for(int i = 0; i < 19; i ++) alledge.insert(a[i]);
int c = 0;
for(int i = 1; i <= N; i ++)
for(int j = 1; j <= N; j ++) {
if(mp[i][j] == 0) return false;
if(book[mp[i][j]] == 0) {
if(alledge.count(mp[i][j]) == 0) return false; //保证22个小正方形均用完
c ++;
book[mp[i][j]] = 1;
if(is_ok(i, j) == false) return false;
}
}
return c == 22; //保证22个小正方形均用完
}
int main() {
for(int x = 1; x <= 47; x ++)
for(int y = 1; y <= 47; y ++) mp[y][x] = 47;
for(int x = 47 + 1; x <= 47 + 46; x ++)
for(int y = 1; y <= 46; y ++) mp[y][x] = 46;
for(int x = 46 + 47 + 1; x <= 46 + 47 + 61;x ++)
for(int y = 1; y <= 61; y ++) mp[y][x] = 61;

DFS(1, 1);
if(judge()) puts("Accept");
}