【电磁】基于Matlab实现理想圆柱形电流片的精确磁场

1 内容介绍

The magnetic field of a cylindrical sheet of current provides a representation of the external field of a cylinder uniformly magnetized along its symmetry axis and an approximation to a helically wound solenoid and is expressible in terms of elliptical integral functions.

2 部分代码

xi_p = z+L/2;

xi_m = z-L/2;

alpha_p=1./sqrt(xi_p.^2+(rho+R).^2);

alpha_m=1./sqrt(xi_m.^2+(rho+R).^2);

beta_p=xi_p.*alpha_p;

beta_m=xi_m.*alpha_m;

g=(rho-R)./(rho+R);

k2_p=(xi_p.^2+(rho-R).^2)./(xi_p.^2+(rho+R).^2);

k2_m=(xi_m.^2+(rho-R).^2)./(xi_m.^2+(rho+R).^2);

k_p=sqrt(k2_p);

k_m=sqrt(k2_m);

K=@(k)ellipticK((1-k.^2));

E=@(k)ellipticE((1-k.^2));

Pi=@(k,g)ellipticPi(1-g.^2,(1-k.^2));

P_1=@(k,g)(K(k)-(2./(1-k.^2)).*(K(k)-E(k)));

P_2=@(k,g)( (1./(g.^2-1)).*(...

g.*(Pi(k,g)-K(k))+g.^2*Pi(k,g)-K(k)) );

B_r=(mu0*M*R./pi)*(alpha_p.*P_1(k_p,g) -alpha_m.*P_1(k_m,g));

B_z=(mu0*M*R./(pi.*(rho+R))).*(beta_p.*P_2(k_p,g)-beta_m.*P_2(k_m,g));

3 运行结果

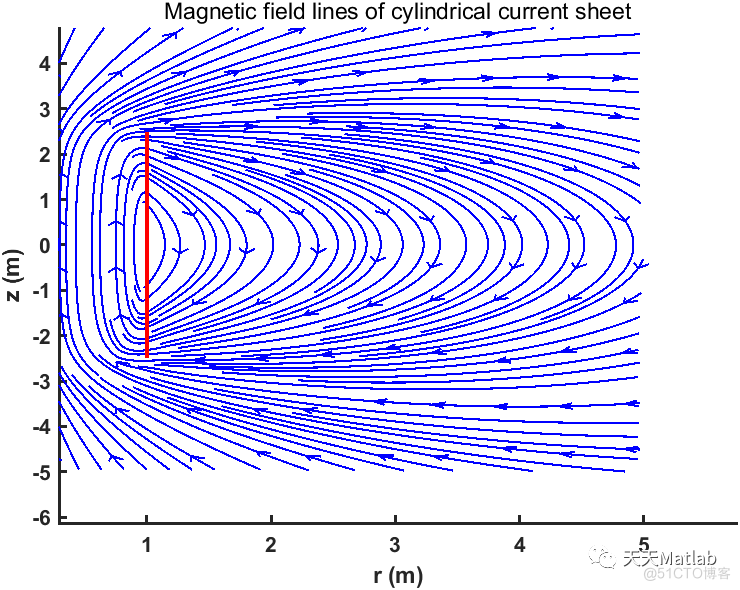
4 参考文献

References

[1] Alessio Caciagli, Roel J. Baars, Albert P. Philipse, Bonny W.M. Kuipers, ''Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization,'' Journal of Magnetism and Magnetic Materials,

Volume 456, 2018, Pages 423-432, ISSN 0304-8853, .

博主简介：擅长​​智能优化算法​​、​​神经网络预测​​、​​信号处理​​、​​元胞自动机​​、​​图像处理​​、​​路径规划​​、​​无人机​​、​​雷达通信​​、​​无线传感器​​等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。